広いダイナミックレンジの信号を調整する回路

図1は,基本的な対数アンプの回路です.入力信号は時間の経過とともに指数関数的に増加する正の電圧です.このときのOUTの出力応答として正しいのは図2の(a)~(d)のうちどれでしょうか.
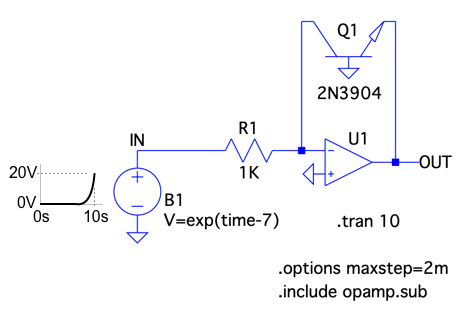
入力信号はe(ネイピア数)を底とする指数関数で増加する正の電圧.
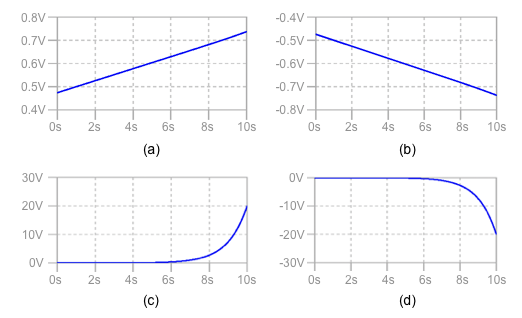
(a)の応答 (b)の応答 (c)の応答 (d)の応答

対数アンプの用途は,入力に広いダイナミックレンジの信号が加わったときアンプ出力を飽和させずに信号処理する回路や信号の対数演算した結果が欲しいときなどに用いられます.
解答は,INの電圧が正のとき,OUTの電圧の極性はどうなるかで絞り込みます.Q1のコレクタ電流(IC1)は,INの電圧とR1で決まります.また,OUTの電圧は,Q1のベース・エミッタ電圧で決まります.この関係を使い,INの電圧が指数関数的に増加したときのOUTの電圧変化を検討すれば分かります.図2の(a)と(b)は,時間とともに1次関数の傾きで変化し,極性が異なります.(c)と(d)は時間とともに指数関数的に変化し,極性が異なります.
INの電圧をVIN,OUTの電圧をVOUTとします.図1は,非反転端子をGNDにした反転アンプの回路です.なので,VINが正の電圧のときVOUTは,負の電圧を出力します.これより図2の(b)または(d)のどちらかになります.
次にVINがeを底とする指数関数で増加したときの出力電圧の応答について検討します.反転端子はバーチャル・グラウンドなので,オームの法則により,VINの変化はR1で電流に変換されます.R1の電流は,VINの変化と同じく指数関数的に増加して,Q1のコレクタ電流となります.Q1のコレクタ電流の変化は,ベース・エミッタ間電圧(VBE1)の変化となり,OUTの電圧は「VOUT=-VBE1」となります.このときQ1のベース・エミッタ電圧は,コレクタ電流を自然対数で圧縮した電圧となります.以上の回路動作によりeを底とする指数と自然対数は逆関数なので,指数関数的に増加する入力信号を自然対数で圧縮した出力電圧となり,出力は時間とともに1次関数の傾きで減少する応答となります.この応答になるのは(b)となります.
●基本的な対数アンプの入出力特性
図1の基本的な対数アンプで,Q1のベース・エミッタ間電圧は,コレクタ電流を自然対数で圧縮した電圧になるということを利用しています.図1のQ1はベース接地なので,コレクタ電流とベース・エミッタ間電圧の関係は式1となります.
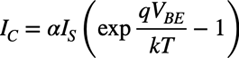 ・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
式1は「VBE>200mV」のとき,誤差が0.05%以下で式2の近似できます.
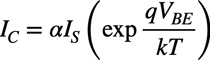 ・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・(2)式2を変形するとVBEとICの関係は式3となります.式3よりVBEは,ICを自然対数で圧縮した電圧になることが分かります.
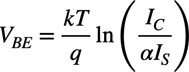 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)次に図1の入出力特性を机上計算します.OPアンプの非反転端子はバーチャル・グラウンドなので,R1の電流は,VINの電圧とR1の抵抗値で決まり,式4となります.
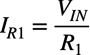 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)OPアンプを理想とすると,R1の電流は,Q1のコレクタ電流となり,式3と式4よりVBEは式5になります.
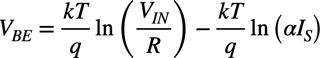 ・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・(5)OUTの電圧は「VOUT=-VBE1」なので,図1の入出力特性は式6となります.
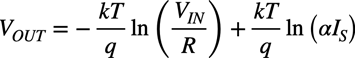 ・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・(6)式6より,図1はVINの変化を自然対数で圧縮した対数アンプとして動作することが分かります.
●基本的な対数アンプのシミュレーション
図3は,図1をシミュレーションした結果です.図3の上段がINの電圧,下段がOUTの電圧です.INの電圧は,時間の経過とともに指数関数的に増大します.対数アンプを通過するとVINの変化は,自然対数で圧縮されるので,OUTの電圧は時間とともに1次関数の傾きで減少する応答となります.この応答が図2の(b)となります.
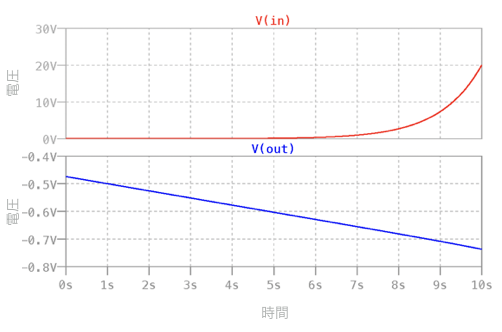
上段は指数関数的に増加する入力信号.
下段は対数アンプの出力電圧.
図3下段の入出力特性は,式6で表されるので,逆方向飽和電流(IS),絶対温度(T),ベース接地電流増幅率(α)によりOUTの電圧が影響を受けます.エミッタ接地アンプの電流増幅率をβとすると,β>100の条件では「α=β/(1+β)」なのでα>0.99となり,出力への影響は僅かです.Tは,温度なので1K(=1℃)変わると「1K/300K=約+3300ppm/℃」の割合で出力電圧は変化します.また,ISはデバイスにより値が変わり,その温度変化は接合温度が10℃上昇すると約倍になることが知られています.このように図1の基本的な対数アンプの出力は,特にTとISの影響が大きく現れ,使いにくい回路となりますので回路の工夫が必要となります.
●実用的な対数アンプの例
図4は,LTspiceのEducationalフォルダにある対数アンプの例です.この回路は図1へR2,R3,Q2,U2,I1を追加したものです.
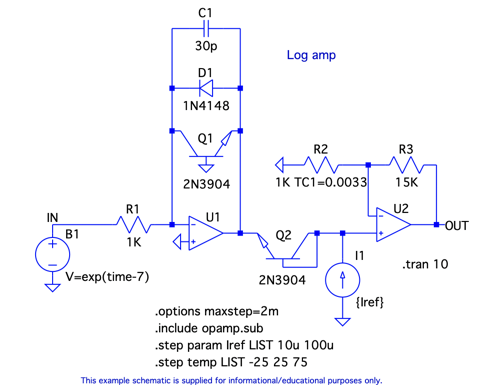
入力信号はeを底とする指数関数で増加する正の電圧.
回路の入出力特性は式7となります.式7の詳しい解説は「IoT時代のLTspiceアナログ回路入門」で配信した「対数増幅回路の入出力特性」を参照してください.
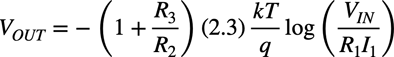 ・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・(7)
図4は,逆方向飽和電流の補償としてQ1とQ2のトランジスタを同じにすることで,ISをキャンセルします.このため式7にISの項はありません.また,絶対温度(T)の温度変化の補償は,R2,R3,U2の非反転アンプのゲイン「1+R3/R2」に温度係数(T)と逆の特性を持たせることで補償します.具体的には,R2を+3300ppm/℃の温度係数を持つ抵抗を使い,「1+R3/R2」の温度変化を約-3300ppm/℃にします.
式7の右辺にある2.3は自然対数を常用対数にする係数です.また「(1+R3/R2)(2.3)(kT/q)=1」になるように「1+R3/R2」のゲインを調整すると,VINが10倍変化したとき VOUTは1Vの変化となります.
D1は,入力電圧が負電圧になったときOPアンプU1の出力飽和防止として働きます.C1は,OPアンプU1の負帰還を安定にするための補償コンデンサです.また,図4のOUTの電圧は,R1I1の電圧で初期値を調整できます.これは広いダイナミックレンジを持つ信号を対数アンプを通して,出力するときのレンジ切り替えなどに使えます.
●実用的な対数アンプのシミュレーション
図5は,図4のシミュレーション結果です.入力信号は,図1と同じ時間の経過とともに指数関数的に増加する正の電圧を印加し,OUTの電圧をプロットしました.I1の電流値となる変数Irefが「.stepコマンド」で10μAと100μAの2通り,周囲温度が「.stepコマンド」で-25℃,25℃,75℃の3通りなので,計6通りのプロットとなります.
VINは,時間の経過とともに指数関数的に増大します.しかし,対数アンプで圧縮されOUTの電圧は,時間とともに1次関数の傾きで減少する応答になります.R2を+3300ppm/℃の温度係数にして回路の温度補償をおこなったので,-25℃,25℃,75℃の各温度でOUTの電圧はほぼ重なっています.また,I1の電流を変えるとOUTの電圧の初期値が調整できることが分かります.
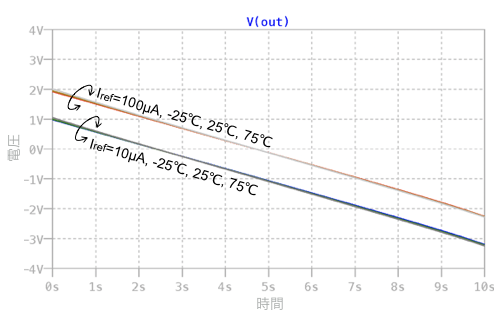
I1を調整してOUTの電圧の初期値を変えることができる.
以上,解説したように, 対数アンプは,ベース・エミッタ間電圧がコレクタ電流を自然対数で圧縮した電圧になることを利用しています.基本的な対数アンプは絶対温度(T)と逆方向飽和電流(IS)の影響を大きく受けるので,図4のように回路で補償する工夫が必要です.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice6_024.zip
●データ・ファイル内容
basic_logamp.asc:図1の回路
basic_logamp.plt:図1のプロットを指定するファイル
logamp.asc:図4の回路
logamp.plt:図4のプロットを指定するファイル
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










