コンデンサの「電圧・電流と時間」の関係

■問題
電気回路 ― 基礎

小川　敦　Atsushi Ogawa

　図1は，1μFのコンデンサ(C₁)に電流源(I₁)が接続された回路です．I₁の初期値は，0AでOut端子の電圧は0Vとなっています．この回路で0AだったI₁の電流を1ns後に1uAになるよう，ステップ状に変化させたとき，Out端子の電圧が1Vになるまでの時間としてもっとも近いのは(a)～(d)のどれでしょうか．

図1　コンデンサに電流源が接続された回路
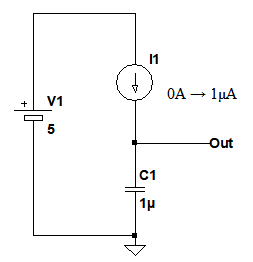
Out端子の電圧が1Vになるまでの時間は?

(a)0.1秒　(b)1秒　(c)3.14秒　(d)6.28秒

■ヒント

　コンデンサの電圧は蓄えられている電荷の量に比例します．そして，コンデンサに一定の電流を加えると，コンデンサの電荷量は時間とともに増加していきます．これらのことを考え合わせると電圧が1Vになるまでの時間を計算することができます．

■解答

(B)1秒

　静電容量値が「C」のコンデンサに「I」という電流を印加したとき，t秒後の電圧は「V=I*t/C」で表されます．この式を変形し，1μFのコンデンサを1μAの電流で充電したとき，電圧が1Vになるまでの時間を求めると「t=1*1μ/1μ=1秒」となります．

■解説

●コンデンサの構造と性質
　コンデンサは，キャパシタとも呼ばれ，電荷を蓄えることのできる素子です．その基本構造は図2のように，絶縁体を2つの電極板で挟んだものです．

図2　コンデンサの模式図
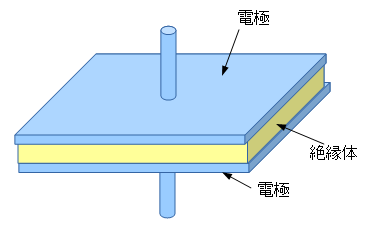
電極と電極の間に電荷を蓄えることができる．

　図2のような構造にすると，電極と電極の間に電荷を蓄えることができます．電荷の量は式1のように電極間の電圧に比例し，その比例定数(C)を静電容量（キャパシタンス）と呼びます．

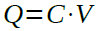・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　静電容量値は電極の面積に比例し，絶縁体の厚さに反比例します．また，電極の間の絶縁体は，誘電体とも呼ばれ，その材質によっても容量値が変わります．

●コンデンサの電圧と電流の関係
　式1は，式2のように変形することができます．式2より電圧は電荷量に比例し，静電容量値に半比例することが分かります．

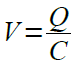・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　一方，電流は，単位時間に移動する電荷の量として定義されています．1秒間に1クーロンの電荷が移動するときの電流値が1Aになります．つまり，電流値（Ｉ）に時間(t)を乗算すると，式3のようにt秒の間に移動した電荷の量が求められます．

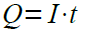・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式2および式3より，静電容量値が「C」のコンデンサに「I」という電流を印加したときの，t秒後の電圧は式4で表されます．

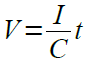・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　コンデンサを一定の電流で充電したとき，特定の電圧になるまでの時間は，式4を変形た式5で求めることができます．1μFのコンデンサを1μAの電流で充電した場合に，コンデンサの電圧が1Vになるまでの時間は，1秒になることが分かります．

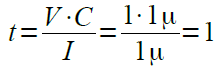・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

●コンデンサを一定電流で充電したときの電圧をLTspiceで確認する
　図3は，コンデンサを一定電流で充電したときの電圧をシミュレーションするための回路です．電流源I₁は，PWL(Piece-Wise Linear) を使用して電流値をステップ状に変化させています．PWL(0 0 1n 1u)とすると，初期値が0Aで1ns後に1μAになります．

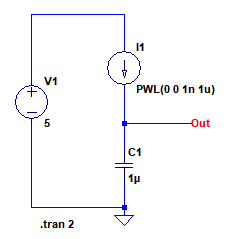
図3　コンデンサを一定電流で充電したときの電圧をシミュレーションするための回路
電流源I₁はPWLを使用して電流値をステップ状に変化させている

　図4は，図3のシミュレーション結果です．1μFのコンデンサを1μAの電流で充電すると，コンデンサの電圧は，直線状に上昇し，1秒後に1Vになることが分かります．

図4　図3のシミュレーション結果
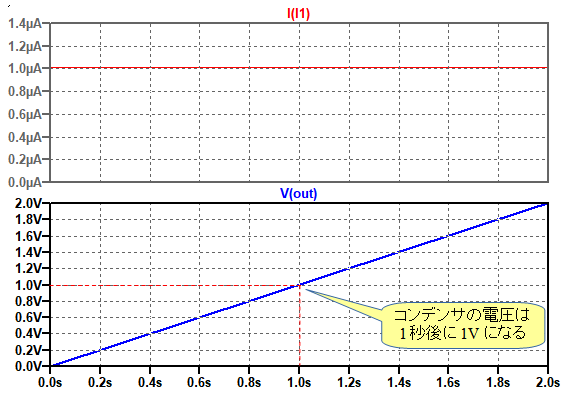
コンデンサの電圧は直線状に上昇し，1秒後に1Vになる．

●コンデンサを定電圧源に接続された抵抗を介して充電したときの電圧をLTspiceで確認する
　図5は，定電流源の代わりに抵抗でコンデンサを充電したときの電圧をシミュレーションするための回路です．電圧源V₁をPWLコマンドにより0Vから5Vにステップ状に変化させます．抵抗(R₁)の値が5MΩなので，抵抗の両端の電圧が5Vのとき，充電電流は1μAになります．

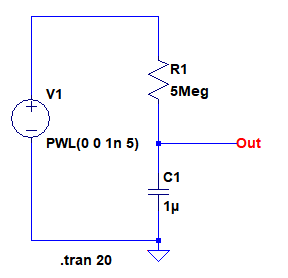
図5　抵抗でコンデンサを充電したときの電圧をシミュレーションするための回路
電圧源V₁をPWLコマンドにより0Vから5Vにステップ状に変化させる．

　図6は，図5のシミュレーション結果です．定電流源で充電したときはコンデンサの電圧は直線状に変化しましたが，定電圧源に接続された抵抗を介して充電した場合は電圧は曲線になり，V₁の電圧に漸近していきます．これは，抵抗を介して充電した場合，その充電電流が徐々に減っていくためです．充電電流は抵抗の両端電圧に比例しますが，コンデンサの電圧が上昇するに従い，抵抗の両端電圧が減少するため，充電電流が減っていくことになります．

図6　図5のシミュレーション結果
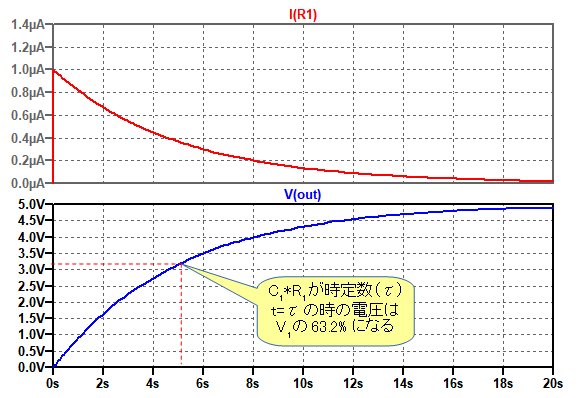
定電圧源に接続された抵抗を介して充電した場合，コンデンサの電圧は曲線になり，V₁の電圧に漸近していく．

　図6の上段が抵抗に流れる電流です．最初は1μAとなっていますが，コンデンサの電圧が上昇するに従い，徐々に減少していくことが分かります．
　図5においてC₁の電圧は，C₁に蓄えられた電荷量(Q)をC₁の容量値で割ったものです．R₁の電圧降下とC₁の電圧を足したものがV₁になります．また，時間(t)における電荷量(Q)は，電流の時間関数(i(t))をt秒間積分したものになります．これらの関係から方程式を立てて解くと，図5の回路のOut端子の電圧は，式6で表されます．

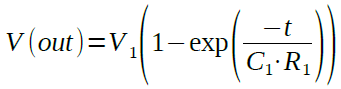・・・・・・・・・・・・・・・・・・・(6)

　この式で，コンデンサと抵抗の値を掛け合わせた「C*R」を時定数(τ)と呼びます．時間tが「C*R」と等しくなったときの出力電圧は，「V(out)=V₁(1-exp(-1))=0.632*V₁」となり，V₁の63.2%の電圧になります．
　このように，コンデンサを充電して電圧を発生させる回路は，定電流充電(図3)の方が，理想に近いのです．しかし，定電流を作るのにトランジスタ等の部品が必要となります．そこで，素子数の少ない回路には，定電圧源と抵抗を使用した充電(図5)が使用されます．一般的にIC内部の回路は，定電流充電を使用し，個別部品を組み合わせて作るような回路は，定電圧源と抵抗を使用した充電回路を使用する傾向にあります．
　以上，コンデンサの電圧と電流の関係について解説しました．コンデンサの充放電による電圧変化を利用した回路には，タイマ回路や発振回路があります．発振回路への応用は「トランジスタからやり直し！LTspiceアナログ電子回路入門025：無安定マルチバイブレータの発振周波数はいくつ？」を参照してください．