直流電源と交流電源

■問題
電気回路 ― 基礎

小川　敦　Atsushi Ogawa

　図1は，1Ωの抵抗(R₁)に色々な波形の電圧を加えることができる回路です．ここで，R₁にV₁，V₂，V₃，V₄のような波形の電圧を加えたとき，R₁で発生する電力の説明として間違っているのは，(a)～(d)のどれでしょうか．

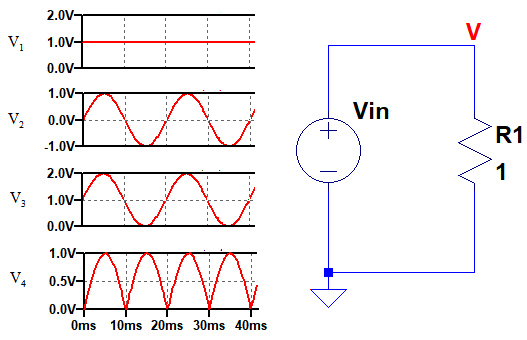
図1　1Ωの抵抗(R₁)に色々な波形の電圧を加えることができる回路

(a)V₁を加えたときの平均電力は，V₂を加えたときの平均電力よりも大きい
(b)V₃を加えたときの平均電力は，V₄を加えたときの平均電力よりも大きい
(c)V₁を加えたときの平均電力とV₃を加えたときの平均電力は等しい
(d)V₂を加えたときの平均電力とV₄を加えたときの平均電力は等しい

■ヒント

　R₁で発生する電力は，印加電圧の2乗を抵抗値で割ったものです．厳密には，それぞれの波形を加えたときの瞬時電力を計算し，その平均値を計算して比較する必要がありますが，波形の特徴をよく考えれば，計算しなくても答えが分かります．

■解答

(c)V₁を加えたときの平均電力とV₃を加えたときの平均電力は等しい

　V₃の波形は，V₂の波形とV₁の波形を足したものです．そのため，V₃を加えたときの平均電力は，V₁を加えたときの平均電力よりも大きくなります．したがって，(c)の「V₁を加えたときの平均電力とV₃を加えたときの平均電力は等しい」というのは誤りであることが分かります．

■解説

●直流と交流の違い
　電源には，直流電源と交流電源があります．直流電源は時間によって，電圧の向きが変化しない電源です．直流電源は，DC(Direct Current)電源とも呼ばれます．直流電源の代表的なものは，乾電池で図1のV₁のように常に一定の電圧が出力されます．
　交流電源は，時間によって電圧の向きが反転する電源です．交流電源は，AC(Alternating Current)電源とも呼ばれます．交流電源の代表は，一般家庭のコンセントから得られる100V電源で，図1のV₂のように，+の電圧と-の電圧が交互に出力されます．
　一般的な電子機器は，直流電源で駆動する必要があります．そのため，交流電源を直流電源に変換する必要があります．家庭用電源が交流になっているのは，交流はトランスを使用することで，電圧の大きさを簡単に変えることができるためです．遠距離に送電するときは，電圧を高くすることで，同じ電力を送るのに必要な電流を小さくし，送電線での無駄な電力の発生を小さくします．そして，家庭に入れるときに安全な電圧まで下げる，ということが，交流を使用することで，簡単にできます．
　図1のV₃の波形は，V₂とよく似ていますが，電圧の大きさが変化しているだけで，向きは一定です．そのため交流ではなく，脈流と呼ばれます．V₄も同様に電圧の向きが変化していないため脈流です．

●抵抗に直流電圧(V₁)を加えたときに発生する電力
　抵抗で発生する電力(W)は，加えた電圧(V)と流れている電流(I)の積で，式1で表されます．

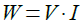・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　ここで抵抗値をRとすると，電流(I)は式2で表されます．

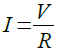・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式2を式1に代入すると，式3のように変形することができます．

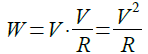・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3より，抵抗で発生する電力は印加電圧の2乗を抵抗値で割ったものであることが分かります．図1のV₁を加えたときの電力は式3を使用して，式4のように1Wと求めることができます．

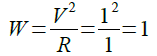・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

●抵抗に直流以外の電圧を加えたときに発生する電力
　抵抗に直流以外の電圧を加えたときに発生する電力も式3を使用して計算することができます．ただし，時間とともに電圧が変化するため，発生電力も時間と共に変化します．直流を加えたときの電力と比較するためには，電力の平均値を求める必要があります．この場合，注意が必要なのは，平均電圧を求めてから電力を計算するのではなく，瞬時電力を計算してから，その平均を計算するということです．

●抵抗に交流電圧(V₂)を加えたときに発生する電力
　V₂の波形は正弦波なので，電圧のピーク値をV_Pとし「x=ωｔ」とすると式5で表されます．

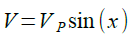・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　瞬時電力は，式6のようになります．

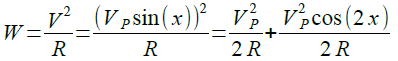・・・・・・・・・・・・・・・(6)

　図2の上段が電圧波形で下段が瞬時電力の波形です．

図2　正弦波交流電圧と瞬時電力波形
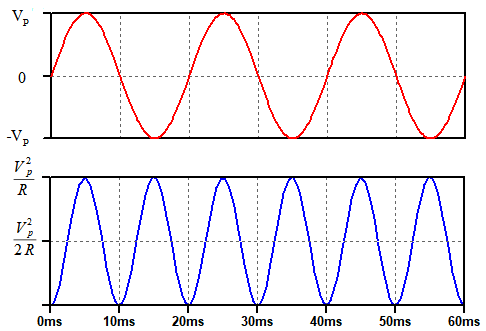
瞬時電力の平均値はV_P²/2Rとなる．

　瞬時電力の波形を見れば分かるように，式6の第二項は平均値を取ると0になるため，電力の平均値は式7で表されます．

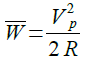・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　図1の定数を当てはめると0.5Wになります．

●抵抗に脈流電圧(V₃)を加えたときに発生する電力
　V₃の波形は，V₂の波形とV₁の波形を足したものです．正弦波電圧のピーク値をV_Pとし「x=ωｔ」とすると式8で表されます．

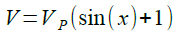・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　瞬時電力は，式9のようになります．

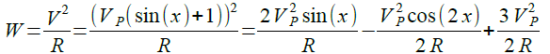・・・・・(9)

　式9の第1項及び第2項は平均値を取ると0になるため，電力の平均値は式10のようになります．

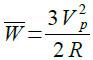・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　図1の定数を代入すると1.5Wになります．

●抵抗に脈流電圧(V₄)を加えたときに発生する電力
　V₄は，V₂の波形の負側の波形を正側に折り返したもので，V₂の半周期の波形が繰り返されています．そのため，平均電力は式6でxが0からπまでの平均で計算できます．式6で0からπまでの平均を取ると第2項は0となるため，平均電力は式7と同じになります．

●抵抗に色々な波形を加えたときに発生する電力のシミュレーション
　図3は，図1の4種類の波形を抵抗に加えたときに，抵抗に発生する電力をシミュレーションするための回路です．

図3　抵抗に色々な波形を加えたときに発生する電力をシミュレーションする回路
V₄の波形はビヘイビア電源を使用し，正弦波の絶対値で作成．

　V₁は，直流電圧を1Vとしています．V₂は，DC offsetを0Vとし，Amplitudeは1VでFreqは50Hzとした正弦波です．V₃は，V₂のDC offsetを1Vとしたものです．V₄の波形は，ビヘイビア電源を使用して作成しています．電源の定義を「V=ABS(sin(2*pi*50*time))」としていますが，sin(2*pi*50*time)で50Hzの正弦波を発生させます．そしてABS()という関数で絶対値を取ることで，図1のV₄のような波形を作成します．

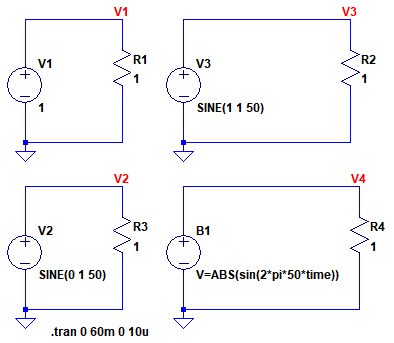
　図4は，直流電圧を加えたときのシミュレーション結果で，上段が電圧波形で，下段が瞬時電力波形です．電力を表示するときは，マウスカーソルを抵抗の上に乗せ，Altキーを押しながらマウス左ボタンをクリックします．直流なので，電圧や電力の時間的変化はなく，発生する電力は1Wであることが分かります．

図4　直流電圧を加えたときのシミュレーション結果
圧や電力の時間的変化はなく，発生する電力は1W．

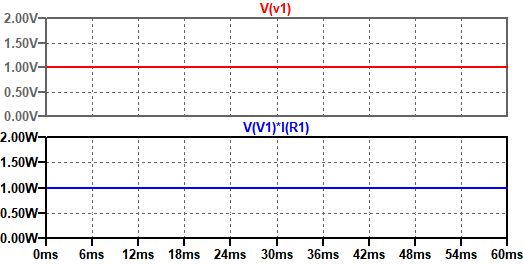
　図5は，V₂の正弦波交流電圧加えたときのシミュレーション結果です．下段が瞬時電力波形です．この波形の平均値を求めるときは，波形上部の文字列をCtrlキーを押しながらマウスボタンをクリックします．平均電力は0.5Wとなっていることが分かります．

図5　正弦波交流電圧を加えたときのシミュレーション結果
平均電力は0.5Wとなっている．

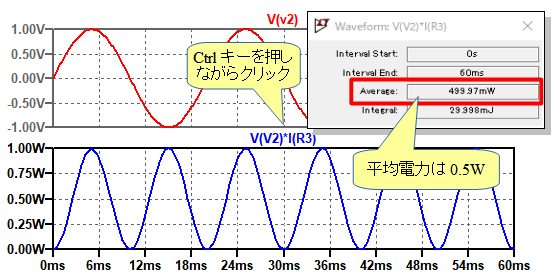
　図6は，V₃の正弦波脈流電圧を加えた特のシミュレーション結果です．平均電力は1.5Wとなっていることが分かります．

図6　正弦波脈流電圧を加えた特のシミュレーション結果
平均電力は1.5Wとなっていることが分かる．

　図7は，V₄の全波整流波形を加えたときのシミュレーション結果です．平均電力は図5と同じく0.5Wとなっていることが分かります．

図7　正弦波脈流電圧を加えた特のシミュレーション結果
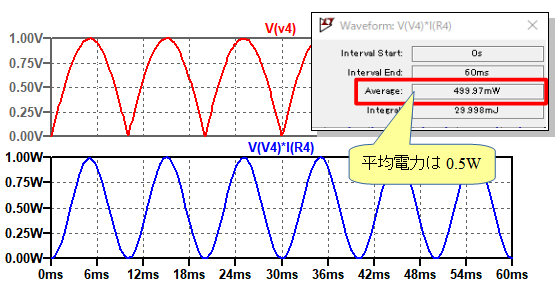
平均電力は1.5Wとなっていることが分かる．

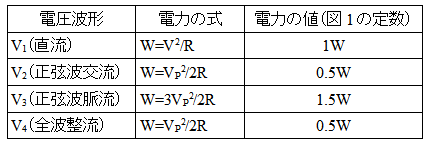
　結果をまとめると，表1のようになります．

表1　V₁，V₂，V₃，V₄の電源のまとめ

　この結果から次のようになります．
(a)「V₁を加えたときの平均電力はV₂を加えたときの平均電力よりも大きい」は正しい．
(b)「V₃を加えたときの平均電力はV₄を加えたときの平均電力よりも大きい」は正しい．
(c)「V₁を加えたときの平均電力とV₃を加えたときの平均電力は等しい」は間違い．
(d)「V₂を加えたときの平均電力とV₄を加えたときの平均電力は等しい」は正しい．

　なお，直流電圧を加えたときと同じ電力を発生する交流電圧を実効値と呼びます．詳細は「LTspice電源＆アナログ回路入門：交流信号による平均電力と実効値」を参照してください．