弛張発振回路の発振周波数が最も低くなる抵抗値はいくつ?

図1は,OPアンプを使った弛張発振回路です.回路は,OPアンプ(LT1022),コンデンサ(C1=0.22μF)と三つの抵抗(R1,R2,R3)から構成しました.抵抗値は,R1を10kΩ,R3を100kΩとし,R2を4種類の抵抗値(10kΩ,22kΩ,47kΩ,100kΩ)でヒステリシス・コンパレータ回路の二つのしきい値(正と負)を変えています.
この回路は,C1の充放電電圧を波形整形し,OUT端子が矩形波の発振となります.弛張発振回路の発振周波数が最も低くなる抵抗値は次の(a)~(d)のうちどれでしょうか.
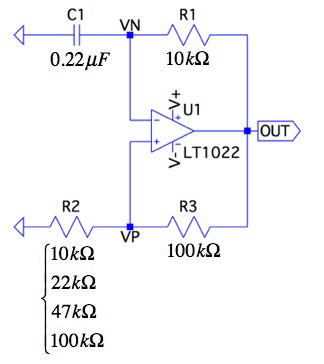
R2を10kΩ,22kΩ,47kΩ,100kΩの4種類とした.
弛張発振回路は,OPアンプの反転端子の充放電電圧(VN)を非反転端子の電圧(VP)で比較し,矩形波の発振として出力します.充放電電圧の時間変化は,抵抗とコンデンサの時定数(τ=R1C1)で決まり,非反転端子のしきい値は,OPアンプとR2,R3からなるヒステリシス・コンパレータ回路の二つのしきい値(正と負)となります.時定数は一定ですので,二つのしきい値により,最も周期が長くなる抵抗値はどれかを考えると簡単にわかります.弛張発振回路は無安定マルチバイブレータとも呼ばれます.
図1の弛張発振回路は,OPアンプとR2,R3からなるヒステシリス・コンパレータ回路に,R1とC1からなる充放電回路を加えたものです.ヒステリシス・コンパレータの出力がHighのとき,R1に流れる電流はC1を充電し,出力がLowのとき,R1に流れる電流は極性が逆になってC1を放電します.C1の充放電の時間変化はOPアンプの反転端子の電圧となります.一方,非反転端子のヒステリシス・コンパレータの二つのしきい値は,出力のHigh/Lowによって切り替わることから,C1の充放電は,二つのしきい値の間で繰り返され,弛張発振回路の出力は波形整形された矩形波の発振になります.
以上の回路動作より,時定数(τ=R1C1)が一定の場合,発振周波数が低くなるのは,C1の充放電波形の周期が長いときです.したがって,二つのしきい値の電圧差が大きいときとなります.
ここで二つのしきい値VHとVLを調べます.OPアンプの正側の最大出力電圧をVOH,負側の最大出力電圧をVOLとし,正帰還の帰還率を式1のβとすると,VHが式2で,VLが式3となります.
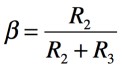 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
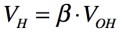 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
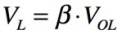 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
VOHとVOLは,OPアンプの最大出力電圧で一定であり,帰還率(β)が大きくなるとVHとVLの電圧差は広がり,発振周波数は低くなります.
(a)~(d)についてβを計算すると次のようになります.
(a)β=10kΩ/(10kΩ+100kΩ)=0.09
(b)β=22kΩ/(22kΩ+100kΩ)=0.18
(c)β=47kΩ/(47kΩ+100kΩ)=0.32
(d)β=100kΩ/(100kΩ+100kΩ)=0.50
したがって,(d)100kΩのとき,発振周波数が最も低くなります.
●OPアンプは正帰還抵抗によりヒステリシス・コンパレータになる
まずヒステリシス・コンパレータ回路から解説します.図2は,図1のR1とC1を削除し,OPアンプの反転端子へ-15Vから+15Vの三角波を入力して,出力の動作を確かめる回路です.図2は,OPアンプの出力からR2とR3の分圧回路を通り,非反転端子へ正帰還しており,出力のHigh/Lowの状態により,GNDを中心に正負のしきい値をもつ,ヒステリシス・コンパレータとして動作します.
図2のしきい値は,正帰還の帰還率をβとすれば,前述の式1であり,正側のしきい値となるVHが式2,負側のしきい値となるVLが式3となります.VOHとVOLはOPアンプの最大出力電圧であり,VOHを13.1V,VOLを-13.1Vとすると,R2とR3が100kΩの場合,VHが6.55V,VLが-6.55Vとなります.
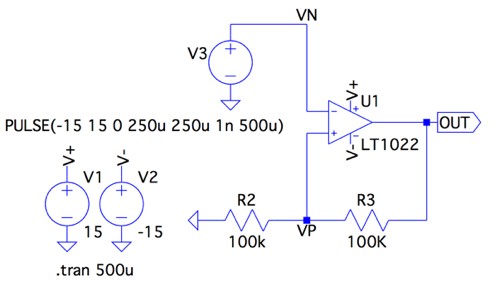
図3は,図2のシミュレーション結果で,横軸を入力電圧,縦軸を出力電圧としました.入力電圧の往復路でしきい値が異なり,ヒステシリスをもったコンパレータとなります.二つのしきい値をカーソルで調べると,計算と一致します.
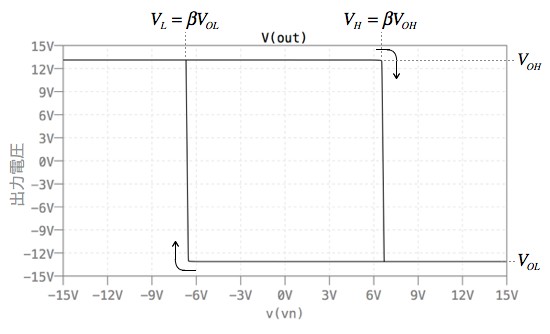
二つのしきい値をもったヒステリシス・コンパレータとして動作している.
●弛張発振回路の発振周波数
図1の弛張発振回路の動作と発振周波数について図4を用いて解説します.図4は,図1の非反転端子,反転端子,出力端子の電圧波形をプロットしたものです.非反転端子の矩形波は,出力のHigh/Lowによって切り替わる二つのしき値の電圧波形です.反転端子の波形は,コンデンサC1の充放電電圧の波形です.出力の波形は,非反転端子のしきい値と比較され波形整形した矩形波となっています.非反転端子のしきい値は,出力電圧のHigh/Lowにより変わるため,反転端子の充放電は二つのしきい値の間で繰り返します.
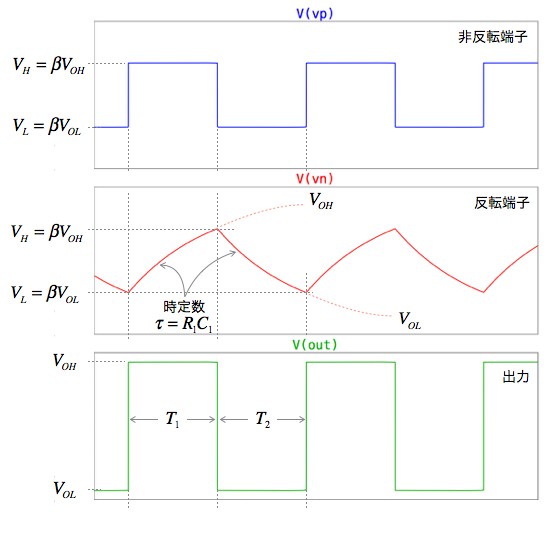
出力の波形は,非反転端子のしきい値と比較され波形整形した矩形波となっているのが分かる.
次に充電しているときの時間T1と,放電しているときのT2について調べ,1周期の時間「T=T1+T2」から周波数を求めます.まず,図1のコンデンサの充電の一般式は式4となります.
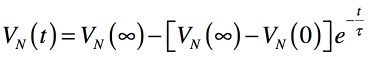 ・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・(4)
VN(t)は,反転端子の電圧の時間変化を表しています.ここで時定数τは式5となります.
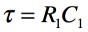 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
なお,抵抗とコンデンサの過渡応答については,「LTspiceアナログ電子回路入門 025 ―― 無安定マルチバイブレータの発振周波数はいくつ?」で詳しく解説されていますので,そちらも参考にしてください.
充電が無限大の時間まで続けば「VN(∞)=VOH」,充電開始の初期電圧は「VN(0)=βVOL」,T1のときは「VN(t)=βVOH」ですので,これらを式4へ代入すると式6となります.
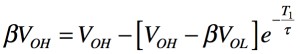 ・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・(6)
式6をT1で整理すると,式7となります.
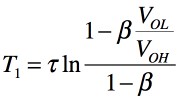 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
同様に放電のときのT2を求めます.充電が無限大の時間まで続けば「VN(∞)=VOL」,充電開始の初期電圧は「VN(0)=βVOH」,T2のときは「VN(t)=βVOL」ですので,式8となります.
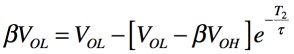 ・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・(8)
式8をT2で整理すると,式9となります.
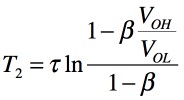 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
ここで「VOH=-VOL」とし,1周期の時間「T=T1+T2」を計算すると,式10となり,発振の周期が求まります.
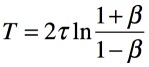 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
式10と図1の回路定数を用い,R2が10kΩ,22kΩ,47kΩ,100kΩの発振周波数「f=1/T」を計算すると次のようになります.
R2=10kΩのときf=1247Hz
R2=22kΩのときf=623Hz
R2=47kΩのときf=343Hz
R2=100kΩのときf=207Hz
式10は時定数が一定の状態で,帰還率βを調整すれば,発振周波数が変わることを示しており,βが大きくなると1周期の時間が長くなって,発振周波数は低くなります.
●弛張発振回路をLTspiceで確かめる
図5は図1をシミュレーションする弛張発振回路です.OPアンプの電源電圧は±15V,R2は「.stepコマンド」で10kΩ,22kΩ,47kΩ,100kΩを切り替えました.
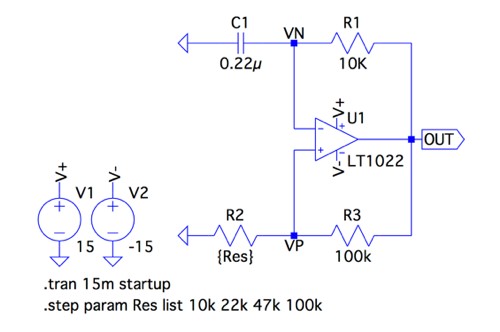
図6は,図5のシミュレーション結果で,抵抗値毎にプロットを分けました.プロットの右横にカーソルで調べた発振周波数を示します.シミュレーションの発振周波数は,式10を用いて計算した結果とほぼ同じであることが確認できます.
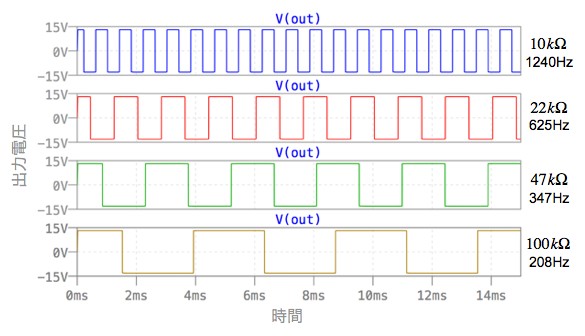
計算した結果とほぼ同じであることが確認できる.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_034.zip
●データ・ファイル内容
Relaxation_Oscillator.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










