DACの働きをする反転加算器の出力電圧はいくら?

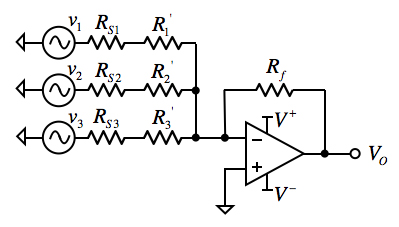
図1は,V1,V2,V3,V4の入力をもつ反転加算器です.回路の抵抗は,R1=8kΩ,R2=4kΩ,R3=2kΩ,R4=1kΩのように2進数の重み付けをしています.負帰還抵抗は,Rf=1kΩとしました.この回路はスイッチをディジタル信号で切り替えることで,4ビットのD-A変換器(DAC)の働きをします.図1は,スイッチで電圧源VrefとGNDを切り替えており「V1=V3=1V」,「V2=V4=0V」の状態です.このときの出力端子(OUT)の電圧は(a)~(d)うちどれでしょうか.
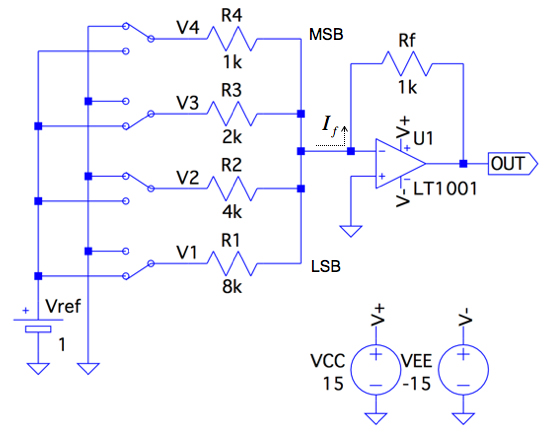
図1のOPアンプの反転端子はバーチャル・グラウンドです.V1,V2,V3,V4の印加電圧によりR1,R2,R3,R4に流れる電流の総和(If)は,負帰還抵抗に流れます.IfはRfにより電圧となって出力されます.
図1の反転端子は,バーチャル・グラウンドであり,R1,R2,R3,R4に流れる電流の総和(If)は式1となります.
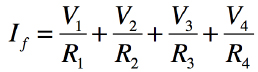 ・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・(1)
OPアンプの反転端子には電流が流れないことから,Ifは負帰還抵抗(Rf)に流れ,式2に示す出力電圧となります.
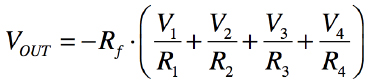 ・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・(2)
図1のV1,V2,V3,V4は「V1=V3=1V」,「V2=V4=0V」ですので,式3のように「-625mV」が出力電圧です.
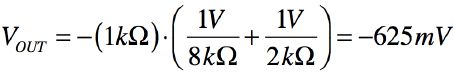 ・・・・・・・・・・・・(3)
・・・・・・・・・・・・(3)
●OPアンプを使った加算器や減算器
OPアンプを使った加算器や減算器の代表的な三つの回路について解説します.代表的な三つの回路は,入力と出力の極性が反転する反転加算器(図2),入力と出力の極性が同じの非反転加算器(図3),加算と減算をする加減算器(図4)です.加算器や減算器は,複数ある信号の加減算や信号の直流電圧を変えるレベル・シフト回路,また出題のように直流電圧の加算などに使われます.信号の直流電圧を変えるレベル・シフトについては,A-Dコンバータの入力電圧範囲に合わせるために使われます.詳しくは「LTspice電子回路マラソン027 ―― 単電源またはレール・ツー・レールOPアンプが必要な回路はどっち?」をご参照ください.
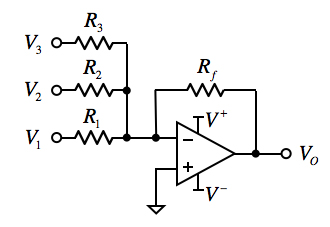
図2の入力と出力の極性が反転する反転加算器は,3入力(V1,V2,V3)の反転加算器の例であり,解答と同様な計算より,出力電圧は式4となります.また「R1=R2=R3=Rf」のときは式5となります.このようにV1,V2,V3の電圧を加算し,出力は加算後の値を反転して出力する反転加算器として働きます.問題の図1は,この反転加算器の応用回路です.
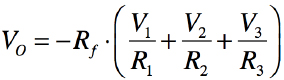 ・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・(4)
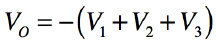 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
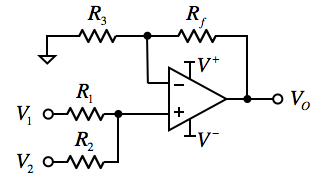
図3の入力と出力の極性が同じの非反転加算器は,2入力(V1,V2)の非反転加算器の例です.出力電圧は,重ね合わせの理より式6となります.また「R1=R2=R3=Rf」のときは式7となります.V1,V2の電圧を加算して出力する非反転加算器として働きます.
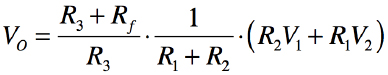 ・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・(6)
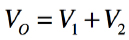 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
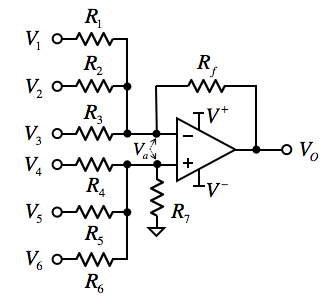
図4の加算と減算をする加減算器は,6入力(V1,V2,V3,V4,V5,V6)の加減算器の例です.OPアンプのバーチャル・ショートの電圧をVaとすれば,OPアンプの非反転端子と反転端子のキルヒホッフの法則より式8が成り立ちます.「Ra=(R4||R5||R6||R7)」,「Rb=(R1||R2||R3||Rf)」とすれば,出力電圧は式9となります.V1,V2,V3の電圧を加算する機能と,V4,V5,V6の電圧を減算する機能の二つを持った加減算器となります.
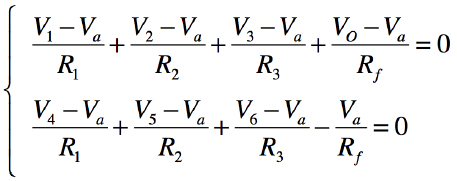 ・・・・・・・・・・・・(8)
・・・・・・・・・・・・(8)
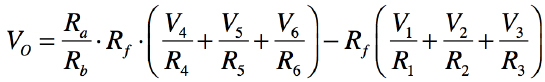 ・・・・・・(9)
・・・・・・(9)
●加算器出力の誤差
図2,図3,図4の回路で抵抗に関わる出力の誤差要因は,次の二つが考えられます.
(1)信号源抵抗があるため出力電圧に誤差が生じる
(2)抵抗比が大きくなると精度良い比を作ることが困難であることから出力電圧に誤差を生じる
(1)の信号源抵抗があるときの等価回路は,反転加算器を例にとると図5となります.RS1,RS2,RS3は,V1,V2,V3の信号源抵抗です.各々の信号源抵抗はR1’,R2’,R3’に直列に接続されるため,式4のR1,R2,R3は「R1=R1’+RS1」,「R2=R2’+RS2」,「R3=R3’+RS3」となり出力電圧に誤差が生じます.図1では,更にスイッチのオン抵抗も加わります.
(2)の抵抗比が大きな場合は,図1のR1,R2,R3,R4のように,各々の抵抗の絶対値が違うと,精度良い抵抗比を作りにくいことが挙げられます.図1の反転加算器を使ったDACは,抵抗で2進数の重み付けをするため,ビット数をnとすれば,最下位ビット(LSB)の抵抗値は「1kΩ×2(n-1)」です.仮に12ビットのDACとすると,LSBの抵抗値は2.048MΩと大きくなり,最上位ビット(MSB)の1kΩとでは,精度の良い比を作ることは困難となります.その他,OPアンプに関わる入力オフセット電圧や入力バイアス電流,CMRR等が原因の出力誤差があります.また,出力を発振させない対策等は,反転増幅器や非反転増幅器と同じです.
●LTSpiceで出力電圧を確かめる
図6は,反転加算器(図1)をシミュレーションする回路です.スイッチはB0~B3の4ビットの電圧で切り替え,4ビットDACの動作をシミュレーションし,反転加算器の入力電圧が「V1=V3=1V」,「V2=V4=0V」の出力電圧をプロットより読み取ります.
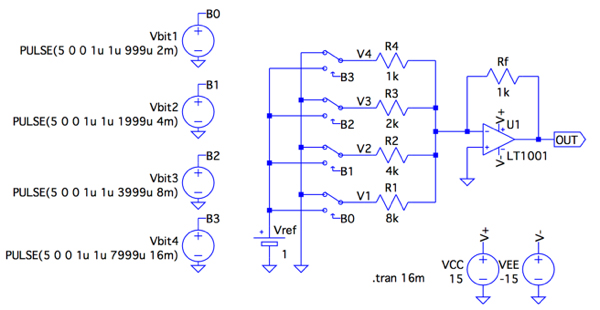
4ビットDACとしてシミュレーションしている.
図7は,図6のシミュレーション結果で,図7(a)は出力電圧,図7(b)はB0~B3の4ビットのディジタル信号です.図7(b)の反転加算器の入力電圧が「V1=V3=1V」,「V2=V4=0V」となるときの,図7(a)の出力電圧は「-625mV」であり解答と同じであることが確かめられました.
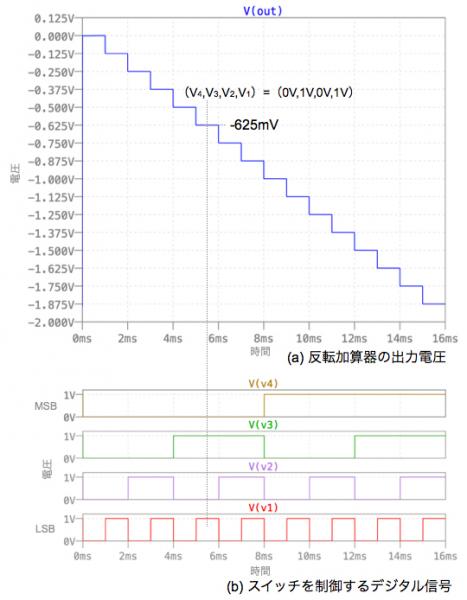
●反転加算器を使った高分解能のDAC
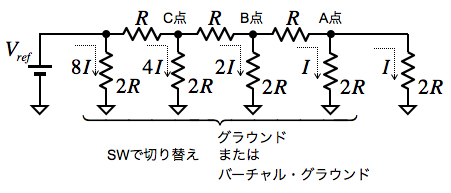
反転加算器を使った応用例として,図1に示したDACがあります.しかし,前述したとおり2進数の重み付けをした抵抗でDACを高分解能とするためビット数を多くすると,正確な抵抗比を実現しにくい問題があります.この場合は,抵抗値に重み付けをする方式ではなく,図8に示すR-2Rラダーを用います.
図8のR-2Rラダーは,反転加算器のバーチャル・グラウンドへ流す電流に2進数の重み付けをおこないます.抵抗は「R」と2倍の「2R」しか使わないので,正確な抵抗比を作りやすくなります.
R-2Rラダーは,A点から右側をみると抵抗値「2R」の並列であり,A点からは同じ電流「I」が分流します.また,A点から右側をみた合成抵抗は「R」となります.次にB点から右側をみると,同じく抵抗値「2R」の並列であり,B点からも同じ電流「2I」が分流し,B点から右側をみた合成抵抗は「R」です.この関係はC点から右側をみても同じであり,ビット数を多くしてもこの関係が続きます.
R-2Rラダーと反転増幅器を使った4ビットDACのシミュレーション回路は,図9です.R1,R2,R3,R4に流れる電流は,図8のように2進数の重み付けがされており,スイッチを切り替えることにより,Ifが変わって出力電圧も変化します.
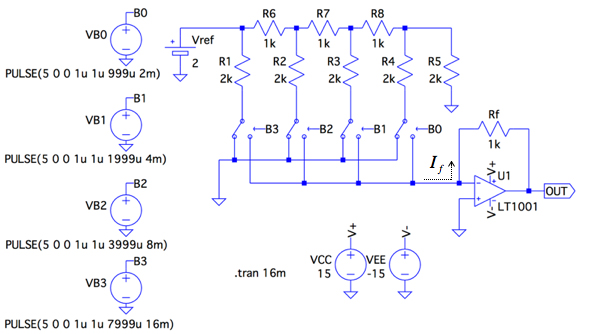
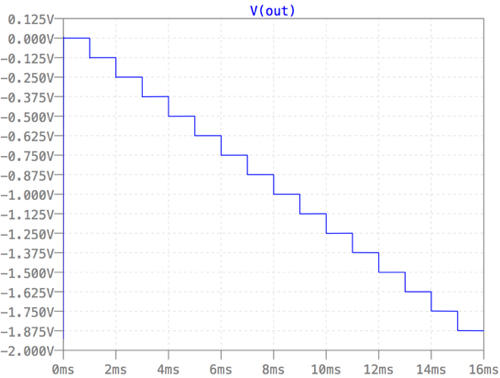
図10は,図9のシミュレーション結果です.出力は問題の図1と同じになりました.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_028.zip
●データ・ファイル内容
DAC_4bit.asc:図6の回路
DAC_4bit_R_2R.asc:図9の回路
TransferSW.asc:スイッチのサブサーキット
TransferSW.asy:スイッチのシンボル
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










