完全差動アンプを使ったロー・パス・フィルタ

■問題

【 LTC1992 】

平賀　公久　Kimihisa Hiraga

　図1(a)は完全差動アンプ(LTC1992)を使い，図1(b)はOPアンプを使った，ロー・パス・フィルタです．図1(a)の周波数特性(V_1a～out+，V_1b～out-)と，図1(b)の周波数特性(V₁～out)を同じにするには，図1(a)のコンデンサC₂とC₃の値を表1の(a)～(d)のどの組み合わせにすればよいでしょうか．

図1　完全差動アンプとOPアンプを使ったロー・パス・フィルタ

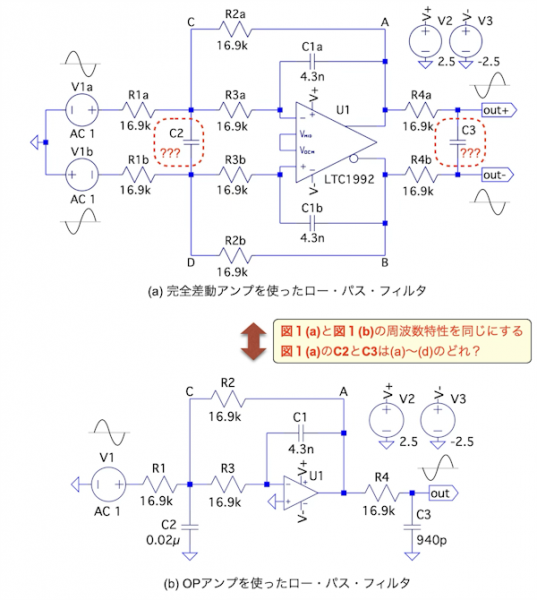
ただし，
図1(a)のV_1aとV_1bの入力信号は同じ振幅で逆相の関係
図1(a)のout+とout-の出力信号は同じ振幅で逆相の関係
図1(a)のV_1aと図1(b)のV₁は同じ振幅で同相の関係

表1　C₂とC₃の値の組み合わせ

	C₂	C₃
(a)	0.005μF	235pF
(b)	0.01μF	470pF
(c)	0.02μF	940pF
(d)	0.04μF	1880pF

■ヒント

　図1(a)と図1(b)の周波数特性は，回路の抵抗とコンデンサで決まります．図1(a)と図1(b)の全ての抵抗は16.9kΩで同じです．図1(a)のC_1aとC_1bは，図1(b)のC₁の4.3nFで同じです．
　同じ周波数特性にするため，図1(b)のC₂とC₃は図1(a)ではどのように設定するのかを検討します．

■解答

	C₂	C₃
(b)	0.01μF	470pF

　図1(a)と図1(b)の全ての抵抗は，16.9kΩで同じです．そして，図1(a)のC_1aとC_1bは，図1(b)のC₁の4.3nFで同じです．周波数特性を同じにする図1(a)のC₂とC₃は，図1(b)のC₂とC₃からどのように変更するかの検討になります．この検討は図1(a)と図1(b)の回路より次のようになります．

図1(b)のC₂とC₃の片方の端子はGNDなので，V₁のシングルエンドの信号に関係する振幅になる
図1(a)のC₂とC₃の両端は，V_1aとV_1bの差動信号により，同じ振幅で同相と逆相の2つの信号が加わるので，図1(b)のC₂とC₃の振幅の2倍になる
この効果により，図1(a)のC₂とC₃の見かけ上のコンデンサ容量は，図1(b)のC₂とC₃の2倍に見える
よって，図1(a)と図1(b)の周波数特性を同じにするには，図1(a)のC₂とC₃を，図1(b)のC₂とC₃の半分のコンデンサ容量にすれば良い
これより，図1(a)のC₂が図1(b)の半分の「0.02μF/2=0.01μF」，C₃が図1(b)の半分の「940pF/2=470pF」になる

　これらの検討から，(b)が正解になります．図1(a)と図1(b)は，LTC1992⁽¹⁾のデータシートのP29にあるアプリケーション回路になります．

■解説

●OPアンプのアプリケーションを参考に作成する
　完全差動アンプのアプリケーション回路は，OPアンプのアプリケーション回路を参考に作成できます．簡単な例として，図2(a)が，OPアンプに負帰還をかけたアンプで，図2(b)が完全差動アンプに負帰還をかけたアンプになります．図2(a)は，R_gとR_fで信号ゲイン「G=-R_f/R_g」が決まります．図2(b)の完全差動アンプは，差動入力と差動出力があり，R_gとR_fで信号ゲイン「G=-R_f/R_g」が決まります．この例のように，図2(a)のin～outの経路にある抵抗を，図2(b)のin-～out+とin+～out-の経路の2つで同じ配置にすると，完全差動アンプのアプリケーションになります．

図2　OPアンプと完全差動アンプを使った負帰還アンプの比較

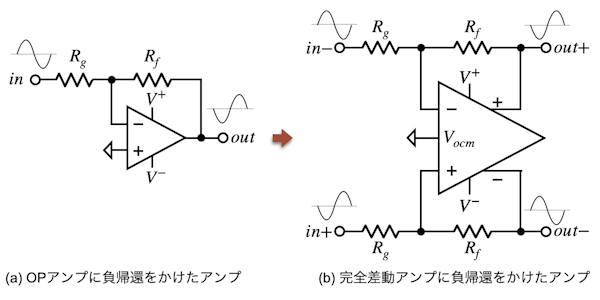
　これと同じ考え方で，図1(a)は，図1(b)のロー・パス・フィルタから作成しています．図2(a)と図2(b)の機能として違うところは，図2(b)の完全差動アンプはV_ocmに直流電圧を加えると，out+とout-の出力同相電圧が変わり，直流のレベル・シフトができる点になります．図2(b)の回路は，「LTspiceとデータシートで学ぶ実践アナログ回路 042　シングルエンド入力信号を差動出力信号にするドライバ」に詳細があります．こちらも参考にしてください．

●OPアンプのロー・パス・フィルタ
　図3は，図1(b)をシミュレーションする回路になります．ここでは図3を使ってOPアンプを使ったロー・パス・フィルタの周波数特性として，低周波の通過域のゲインとコーナ周波数について机上で検討します．その後シミュレーションで特性を確かめます．図3のOPアンプは，LTspiceの部品ライブラリにある理想OPアンプ（UniversalOpAmp1）を使用しています．

図3　OPアンプを使ったロー・パス・フィルタ

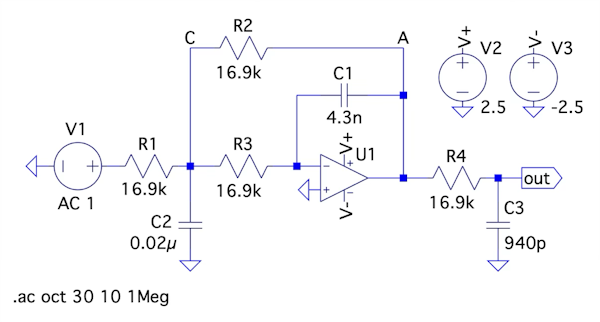
　図3は，入力のV₁～ラベルAで示したOPアンプ出力までが2次のロー・パス・フィルタになります．そしてラベルA～outがR₄とC₃を使った1次のロー・パス・フィルタで構成しています．図3のV₁～outの全体の伝達関数は式1になります．

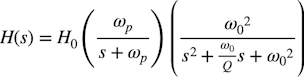・・・・・・・・・・・・・・・・・・・・(1)

　式1のH₀は，ロー・パス・フィルタの通過域である低周波のゲインを表し，式2になります．式2へ図3の抵抗値を入れるとゲインは「H₀=1倍」になります．

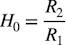・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式1のf₀は，2次のロー・パス・フィルタ（V₁～ラベルA）のコーナ周波数を表し，式3になります．式3へ図3の抵抗値とコンデンサ値を入れるとコーナ周波数は「f₀=1kHz」になります．

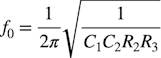・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式1のQは，2次のロー・パス・フィルタ（V₁～ラベルA）のフィルタ特性のQを表し，式4になります．式4へ図3の抵抗値とコンデンサ値を入れると「Q=0.719」になります．フィルタ特性で「Q=0.707」のときは，バターワース特性になります．これより，図3はバターワース特性に近くなり，通過域のゲインから-3dBになる周波数が，式3のコーナ周波数f₀になります．

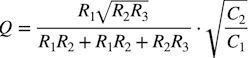・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式1のf_pは，ラベルA～outのR₄とC₃を使った1次のロー・パス・フィルタのコーナ周波数を表し，式5になります．式5へ図3の抵抗値とコンデンサ値を入れると，コーナ周波数は「f_p=10kHz」になります．

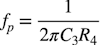・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　次に机上計算とシミュレーション結果の比較をします．図4は，図3のシミュレーション結果で「.ac」コマンドで10Hz～1MHz間を周波数が2倍あたり30ポイントでスイープした周波数特性になります．図4の上段はV₁～outの全体の周波数特性，図4の下段は，R₄とC₃を使った1次のロー・パス・フィルタの特性を見やすくするため，ラベルA～outの周波数特性「V(out)/V(a)」を別にプロットしました．

図4　図3のシミュレーション結果
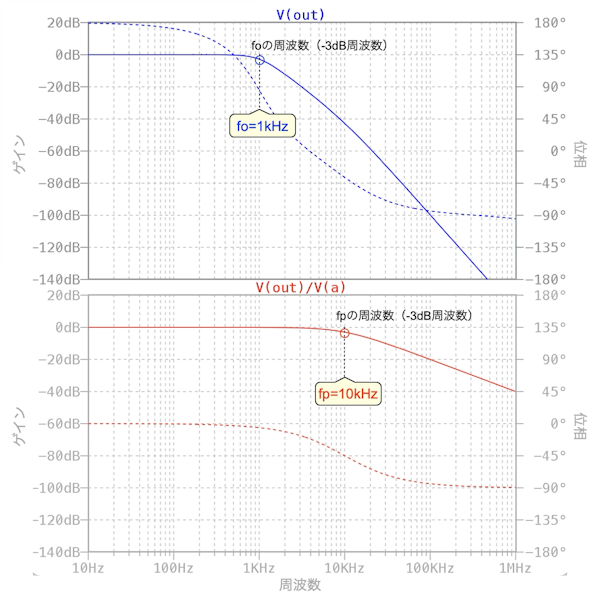
低周波の通過域のゲインが0dB（1倍），f₀が1kHz，f_pが10kHzになる．

　図4の上段より，通過域である低周波のゲインは0dBなので，式2で求めた「H₀=1倍」になるのが分かります．V₁～ラベルAの2次のロー・パス・フィルタのコーナ周波数は「f₀=1kHz」であり，式3で求めた周波数と同じになります．R₄とC₃を使った1次のロー・パス・フィルタのコーナ周波数は「f_p=10kHz」であり，式5で求めた周波数と同じになります．このように机上計算とシミュレーションは一致することが確認できます．

●完全差動アンプのロー・パス・フィルタを検討
　解説の最初にある図2(a)から図2(b)への応用で述べた通り，完全差動アンプのアプリケーション回路は，OPアンプを使ったアプリケーション回路から作成できます．そのフィルタ回路例として挙げたのが，図1(a)の完全差動アンプを使ったロー・パス・フィルタで，これは図1(b)のOPアンプを使ったロー・パス・フィルタからの応用になります．
　図5は，図1(b)のOPアンプを使ったロー・パス・フィルタを元にして，抵抗とコンデンサを正確に完全差動アンプへ適用した回路です．この回路は図1(b)と同じ周波数特性のロー・パス・フィルタとして動作しますが，コンデンサの部品数が多くなります．

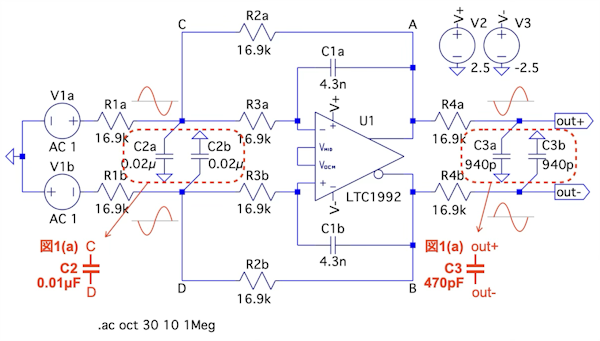
図5　OPアンプを使ったロー・パス・フィルタを完全差動アンプに適用した回路

　ここで，図5の「C_2a，C_2b」と「C_3a，C_3b」に注目すると，図5の「C_2a，C_2b」は，図1(a)のラベルCとラベルD間にあるC₂に置き換えることができます．また，図5の「C_3a，C_3b」は，図1(a)のout+とout-間にあるC₃で置き換えることができます．注意点として図1(a)のC₂とC₃に置き換えるとコンデンサ値の変更が必要になります．具体的には，図1(a)と図1(b)を用いて検討すると次になります．

図1(b)のC₂とC₃の片方の端子は，GNDなので，V₁のシングルエンドの信号に関係する振幅になります
図1(a)のC₂とC₃の両端は，V_1aとV_1bの差動信号により，同じ振幅で同相と逆相の2つの信号が加わるので，図1(b)のC₂とC₃の振幅の2倍になります
この効果により，図1(a)のC₂とC₃の見かけ上のコンデンサ容量は，図1(b)のC₂とC₃の2倍に見えます
よって，図1(a)と図1(b)の周波数特性を同じにするには，図1(a)のC₂とC₃を，図1(b)のC₂とC₃の半分のコンデンサ容量にします

　これらの検討を使って解答の答え合わせをすると，図1(a)のコンデンサは「C₂= 0.02μF/2=0.01μF」,「C₃=970pF/2=470pF」になり，(b)が正解になります

●完全差動アンプを使ったロー・パス・フィルタを確認
　図6は図1(a)の完全差動アンプを使ったロー・パス・フィルタの周波数特性をシミュレーションする回路になります．シミュレーションの設定は図3と同じです．

図6　完全差動アンプを使ったロー・パス・フィルタ

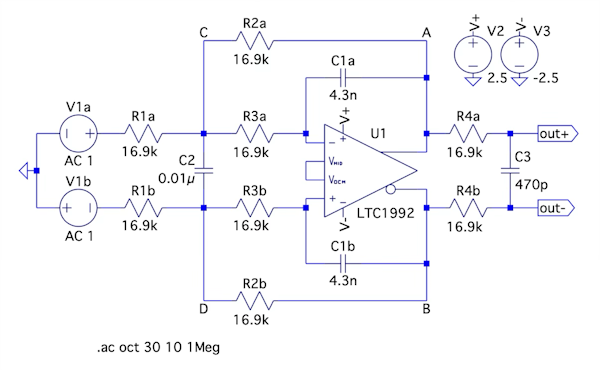
　図7は，図6のシミュレーション結果です．図7の上段はV_1a～out+とV_1b～out-の全体の周波数特性，図7の下段がラベルA～out+とラベルB～out-の1次のロー・パス・フィルタの周波数特性になります．

図7　図6のシミュレーション結果
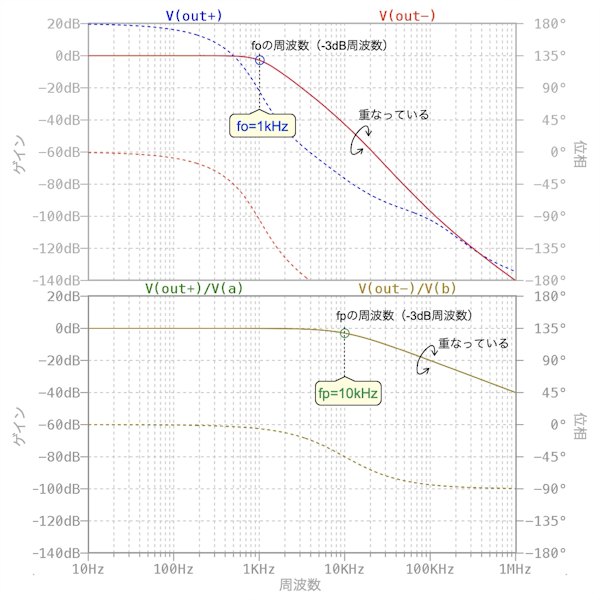
H₀は0dB，f₀は1kHz，f_pは10kHzとなり，図3のシミュレーション結果である図4と同じ周波数特性になる．

　図7の上段より，通過域である低周波のゲインは0dBなので，H₀のゲインは「H₀=1倍」，f₀のコーナ周波数は「f₀=1kHz」，f_pのコーナ周波数は「f_p=10kHz」になります．このプロットは，図3のOPアンプを使ったロー・パス・フィルタのシミュレーション結果である図4のプロットと一致するのが分かります．

●ロー・パス・フィルタで出力同相電圧を変える
　最後に，完全差動アンプを使ったロー・パス・フィルタで出力同相電圧を決めるV_ocmが変化したときの過渡応答について「.tran」コマンドを使ってシミュレーションで確かめます．
　図8は，図1(a)の過渡応答をシミュレーションする回路になります．

図8　V_ocmで出力同相電圧を変化させたシミュレーション回路
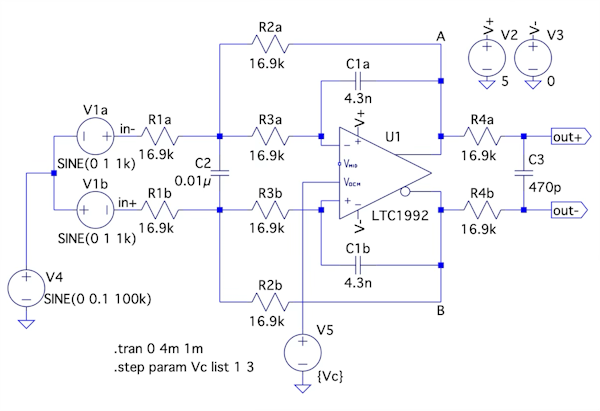
V_ocmは1Vと3Vの2種．
入力信号は振幅が1V，周波数が1kHzの差動入力信号に，同相雑音として100kHzの正弦波を重畳している．

　差動入力信号のV_1a，V_1bは周波数が1kHz，振幅が1Vの正弦波で逆相の信号になります．同相雑音としてV₄の信号源から周波数が100kHz，振幅が0.1Vを重畳しています．出力同相電圧を決めるV_ocmは「.step」コマンドを使い1Vと3Vの2種になります．
　図9は，図8のシミュレーション結果になります．図9の上段は，in+とin-のラベルでプロットした差動入力信号です．図9の下段は，out+とout-のプロットになります．図9の上段の差動入力信号は，周波数が1kHz，振幅が1Vの信号に，雑音分として周波数が100kHz，振幅が0.1Vが重畳した信号になります．
　図9の下段は，out+とout-の信号で，ロー・パス・フィルタにより雑音を除去した差動出力信号になります．そして，V_ocmが1Vのとき出力同相電圧は1V，V_ocmが3Vのとき出力同相電圧は3Vになり，出力は直流のレベル・シフトができることが分かります．

図9　図8のシミュレーション結果
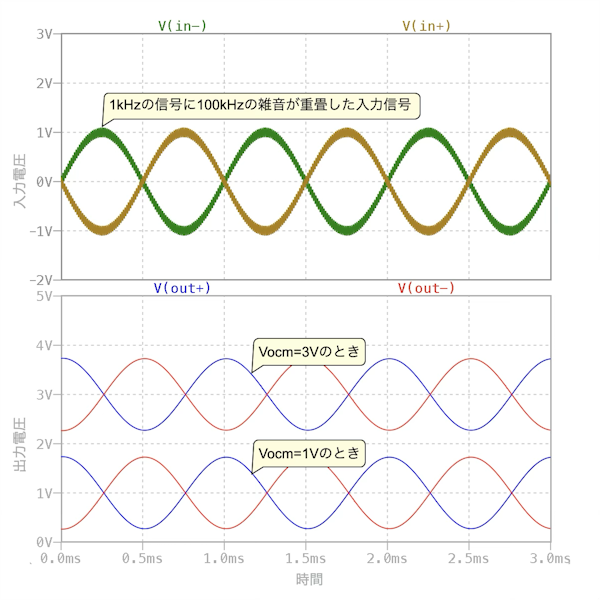
V_ocmにより出力同相電圧が変わり，直流レベル・シフトができる．
100kHzの雑音はロー・パス・フィルタで除去される．

　以上，完全差動アンプを使ったロー・パス・フィルタはOPアンプを使ったロー・パス・フィルタから作成できます．その他にも積分回路や交流結合のアンプなど，OPアンプの回路を完全差動アンプの回路に応用して作る例がデータシートに記載されていますので参考にしてください．

◆参考・引用*文献
(1) LTC1992のデータシート：アナログデバイセズ

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice11_044.zip

●データ・ファイル内容
LPF ac.asc：図3の回路
LPF ac.plt：図3のプロットを指定するファイル
fully differential amplifier LPF ac.asc：図6の回路
fully differential amplifier LPF ac.plt：図6のプロットを指定するファイル
fully differential amplifier LPF tran.asc：図7の回路
fully differential amplifier LPF tran.plt：図7のプロットを指定するファイル