周波数特性への影響が低い高ゲインのTIA

■問題

【 ADA4625-1，ADA4350 】

平賀　公久　Kimihisa Hiraga

　図1(a)と図1(b)は，トランスインピーダンス・アンプ(Transimpedance Amplifier：TIA)です．フォト・ダイオードの電流信号を電圧に変換してoutから出力します．
　図1(a)は，R_f，R₁，R₂の等価抵抗とC_fで，抵抗端子間の容量による周波数特性への影響が低く対策した，ゲイン1MΩのTIAです．
　図1(b)は，R_f1の抵抗とC_f1で，抵抗端子間の容量による周波数特性への影響を受けやすい，ゲイン1MΩのTIAです．具体的には,図1(b)の周波数特性を決めるC_f1は0.5pFと低く，R_f1の抵抗端子間の容量がC_f1に近い値，またはそれ以上になると周波数特性が変わります．
　そこで，対策した図1(a)の周波数特性を図1(b)の周波数特性に近づけるには，図1(a)のC_fの値を(a)～(d)のどれにすればよいでしょうか．

図1　フォト・ダイオードの電流信号を電圧にするTIA回路
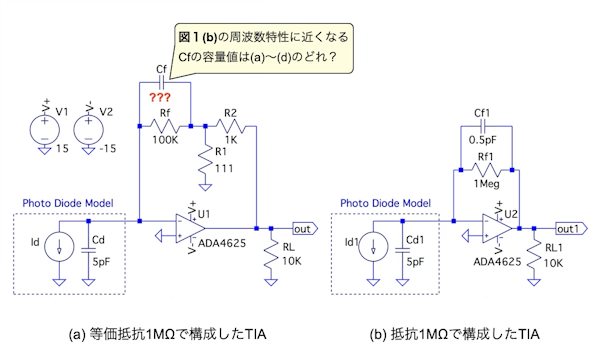
フォト・ダイオードは波線で囲ったモデルで表している．
図1(b)の周波数特性に近くなる図1(a)のC_fの値は(a)～(d)のどれ？

(a) 4.7pF　(b) 10pF　(c) 15pF　(d) 20pF

■ヒント

　図1(a)の周波数特性を図1(b)に近づけるには，図1(a)のOPアンプの反転端子とout間のインピーダンス周波数特性を，図1(b)のOPアンプの反転端子とout1間のインピーダンス周波数特性に近づけ，TIAの信号ゲインの周波数特性が同じになるようにします．これをヒントに検討して下さい．

■解答

(a) 4.7pF

　図1(a)と図1(b)の信号ゲイン伝達特性を計算し，図1(a)と図1(b)のコーナ周波数が近くなるように図1(a)のC_fを調整します．

図1(a)の計算

図1(a)のC_fとR_fの合成インピーダンスをZ_fとする
低周波からコーナ周波数付近まではZ_f＞＞R₂の大小関係なので，図1(a)の信号ゲイン伝達特性は,「v_out/I_d≒[-R_f/(1+sC_fR_f)]*(1+R₂/R₁)」の近似になる
このときのコーナ周波数は「f_P≒1/(2πC_fR_f)」になる

図1(b)の計算

図1(b)の信号ゲイン伝達特性は，「v_out1/I_d1=-R_f1/(1+sC_f1R_f1)」になり，コーナ周波数は「f_P1=1/(2πC_f1R_f1)」である．

図1(a)と図1(b)のコーナ周波数の計算結果より

コーナ周波数を「f_P=f_P1」にすると，図1(a)と図1(b)の周波数特性は近くなる
図1(a)のR_fは図1(b)のR_f1の1/10なので，図1(a)のC_fは「C_f=C_f1*10倍=5pF」が目安になる
この容量に近いのは(a)の4.7pFになる

　これより，(a) 4.7pFが正解になります．図1(a)のC_fは図1(b)のC_f1より約10倍の容量なので，図1(a)のR_fと図1(b)のR_f1に同程度の抵抗端子間容量がついたとき，図1(a)の方が周波数特性への変化の影響が低くなります．

■解説

●高いゲインのTIAは抵抗端子間容量の影響を受ける
　図1(b)のTIAは部品が少なく一般的に使われる回路です．図1(b)はOPアンプ，信号ゲインを決める抵抗(R_f1)，信号ゲインの周波数特性と負帰還の安定補償をするC_f1になります．
　回路の特徴として，低い入力電流を高い出力電圧にするような高ゲインの用途ではR_f1の抵抗値が高くなり，C_f1の容量は低くなります．図1(b)では「R_f1=1MΩ」,「C_f1=0.5pF」になります．
　このような高ゲインの用途で使うとき，抵抗端子間の容量で周波数特性に影響が現れるので注意が必要です．
　具体的には，図1(b)のR_f1の抵抗端子間に僅かな容量があり，その端子間容量はC_f1と並列になります．
　実機では基板の配線間の容量も加わり，抵抗端子間の容量は数百fF(0.**pF)になることもあります．このため抵抗の端子間容量がC_f1に近い値，またはそれ以上になるとC_f1に抵抗端子間容量が加わるので，TIAの周波数特性に影響します．

●抵抗端子間容量の影響を低くする対策
　抵抗端子間容量の影響を低くする対策として，図1(a)の回路を使います．図1(a)はADA4350⁽¹⁾のデータシートp36にあるアプリケーション回路で紹介されています．図1(a)を使うと，R_fの抵抗値が低くなり，図1(b)と同じ周波数特性にするときC_fを高くすることができます．C_fが高くなるとR_fの抵抗端子間容量の影響は低くなります．
　アプリケーション回路を紹介しているADA4350は，OPアンプ，スイッチング回路，A-Dコンバータ・ドライバを内蔵したICでLTspiceの部品ライブラリにありません．抵抗端子間容量の影響を受けるのは，単体のOPアンプを使ったときも同じです．そこで，本稿はADA4350に内蔵されているOPアンプに近いものとして，JFET入力OPアンプのADA4625-1⁽²⁾を使いてシミュレーションします．

●抵抗端子間容量の影響を確認する
　ここでは，図1(b)をシミュレーションする図2を使い，抵抗1MΩで構成したTIAの周波数特性をシミュレーションで調べます．C_f1は「.step」コマンドで次のの3種(0.5pF，1.0pF，1.5pF)の値を入れ替えます．

0.5pF：図1(b)の「C_f1=0.5pF」で抵抗端子間容量がないとき
1.0pF：抵抗端子間容量がC_f1と同程度として「C_f1+抵抗端子間容量0.5pF=1.0pF」のとき
1.5pF：抵抗端子間容量がC_f1の2倍あるとして「C_f1+抵抗端子間容量1.0pF=1.5pF」のとき

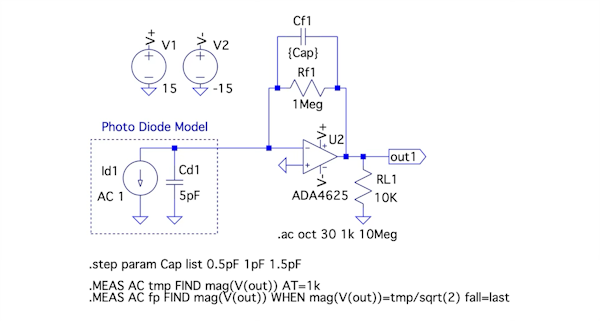
図2　抵抗1MΩで構成したTIAの周波数特性をシミュレーションする回路
C_f1は0.5pF，1.0pF(抵抗端子間容量分として0.5pF)，1.5pF(抵抗端子間容量分として1pF)の3種．

　シミュレーションは「.ac」コマンドで1kHz～10MHz間を周波数が2倍あたり30ポイントでスイープします．信号ゲイン周波数特性のコーナ周波数は「.meas」コマンドを使い，1kHzのゲインから-3dBになる周波数を求めます．
　ここで，図2の回路の信号ゲイン伝達特性は図3になり，そのコーナ周波数についての机上計算式について解説します．図2の信号ゲイン伝達特性の計算式は，OPアンプが理想のとき式1になります．

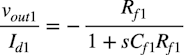・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　式1からOPアンプが理想のときのコーナ周波数の計算式は式2になります．

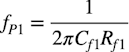・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　図3は，図2のシミュレーション結果です．信号ゲインの周波数特性になります．「.meas」コマンドで調べたコーナ周波数はログ・ファイルに記録されています．ログ・ファイルは回路図上で「Ctrl+L」で開きます．ここではログ・ファイルにある「.meas」コマンドで調べたコーナ周波数を図3に示しました．図3より，コーナ周波数は次になります．

0.5pFのとき431kHz
1.0pF(抵抗端子間容量分0.5pF)のとき197kHz
1.5pF(抵抗端子間容量分1.0pF)のとき116kHz

　このように抵抗端子間の容量がC_f1に近い値，またはそれ以上になると周波数特性に影響を与え，コーナ周波数は大きく変化し，周波数特性のプロットも変化します．

図3　図2のシミュレーション結果
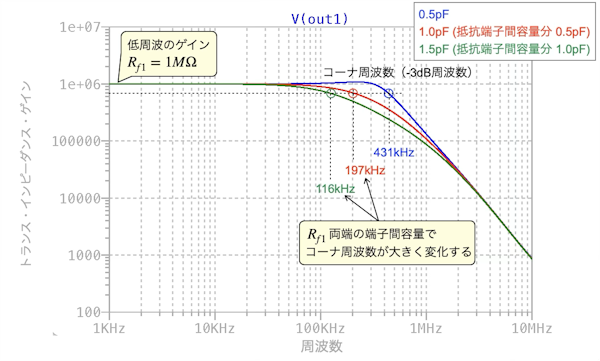
R_f1の抵抗端子間の容量がC_f1に近い値，またはそれ以上になると周波数特性が変化する．

●等価抵抗を計算する
　次に図1(a)の等価抵抗について，図4を使い机上計算します．等価抵抗が分かると図1(a)の信号ゲイン伝達特性が計算できます．図4はY-Δ変換と呼ばれる変換で，図4(a)のY型のネットワークは図4(b)のデルタ型のネットワークと等価になります．図1(a)のR_f，C_f，R₁，R₂を図4(a)に適用すると，Y_aはC_fとR_fの並列のアドミッタンス，Y_bはR₂のアドミッタンス，Y_cはR₁のアドミッタンスになります．Y-Δ変換した図4(b)のY_abが図1(a)の等価抵抗に相当します．

図4　Y-Δ変換（スター・デルタ変換）
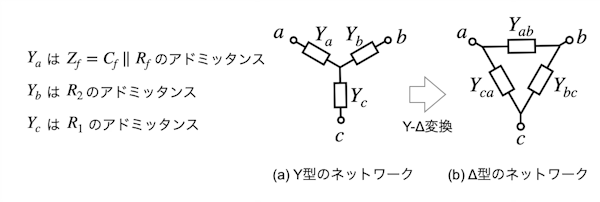
図1(a)のZ_f，R₁，R₂から等価抵抗を求めるためY-Δ変換を使う．

　Y-Δ変換をすると，図4(b)のY_abは式3になります．

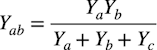・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3中のY_aは，図1(a)のR_f，C_fによる合成インピーダンスZ_fの逆数になります．合成インピーダンスのZ_fは式4になります．

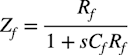・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式3へ「Y_a=1/Z_f」,「Y_b=1/R₂」,「Y_c=1/R₁」のアドミッタンスを代入します．そしてY_abのアドミッタンスをZ_abのインピーダンスで表すと式5になります．

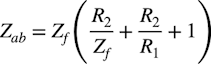・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　ここで図1(a)は，低周波からコーナ周波数付近まではZ_f＞＞R₂の大小関係なので，式5中のR₂/Z_fの値は小さいので無視して近似します．式5のZ_abのインピーダンスは式4を使うと式6の近似になります．

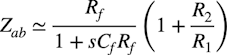・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式6のZ_abが図1(a)の等価抵抗となり，信号ゲイン伝達特性の近似は式7になります．低周波のときは式7のC_fがオープンと考えることができ，低周波の信号ゲインは「R_f*(1+R₂/R₁)=1MΩ」になります．

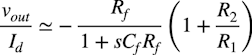・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式7の伝達特性より，図1(a)のコーナ周波数は式8になります．

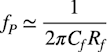・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　ここで解答の確認をします．図1(a)と図1(b)の周波数特性を近くするには，式8のコーナ周波数を式2のコーナ周波数と同じにし,「f_P=f_P1」になるようにします．図1(a)のR_fは図1(b)のR_f1の1/10です．「f_P=f_P1」とするには，図1(a)のC_fは「C_f=C_f1*10倍=5pF」が目安になります．この容量に近いのは(a)の4.7pFになります．
　図1(a)のC_fは，図1(b)のC_f1より約10倍の容量なので，図1(a)のR_fと図1(b)のR_f1に同程度の抵抗端子間容量がついたとき，図1(a)の方が周波数特性の変化が小さくなります．

●等価抵抗1MΩで構成したTIAの確認
　図5は，等価抵抗1MΩで構成したTIAの周波数特性をシミュレーションする回路になります．C_fは「.step」コマンドで解答の候補の4.7pF，10pF，15pF，20pFの4種を入れ替えます．シミュレーションの「.ac」コマンドと「.meas」コマンドは図2と同じになります．

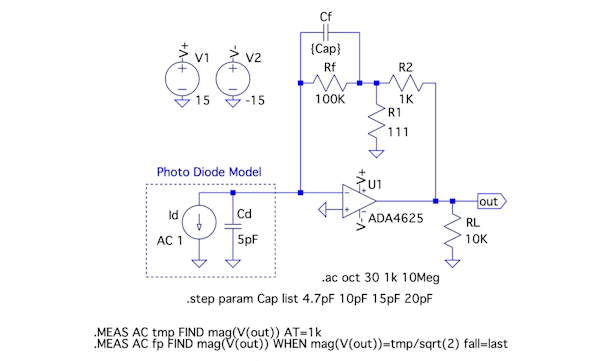
図5　等価抵抗1MΩで構成したTIAの周波数特性をシミュレーションする回路
C_fは0.5pF，10pF，15pF，20pFの4種．

　　図6は，図5のシミュレーション結果になります．「.meas」コマンドで調べたコーナ周波数はログ・ファイルに記録されています．そのコーナ周波数を図6に示しました．
　低周波の信号ゲインは，先程の式7で検討したように1MΩになります．そして，図3の「C_f1=0.5pF」のときのコーナ周波数「f_P1=431kHz」に近いのは，図6の「C_f=4.7pF」の「f_P=394kHz」になります．

図6　図5のシミュレーション結果
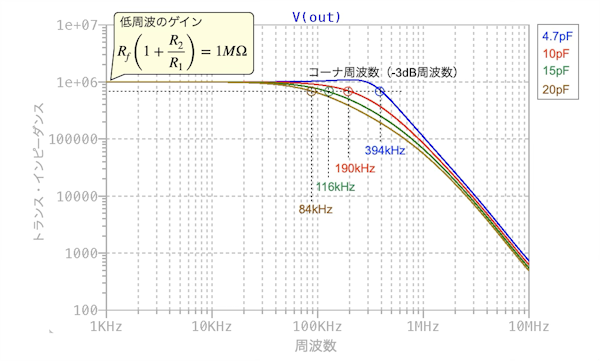
「C_f=4.7pF」のとき，図3の「C_f1=0.5pF」の周波数特性に近くなる．

●等価抵抗のTIAと抵抗のTIAの時間応答を比較
　最後に，等価抵抗(R_f，R₁，R₂)1MΩで構成したTIA[図7(a)]と，抵抗(R_f1)1MΩで構成したTIA[図7(b)]の時間応答を比較します．図7(a)のC_fは解答の「(a) 4.7pF」にしています．フォト・ダイオードの電流(I_d，I_d1)は矩形波の電流(振幅1μA，on時間20μA，周期40μs)です．この電流がTIAに加わったときのoutとout1の時間変化をシミュレーションします．シミュレーションはtran解析で0μs～60μsの過渡解析です．

図7　等価抵抗と抵抗のTIAの時間応答を比較する回路
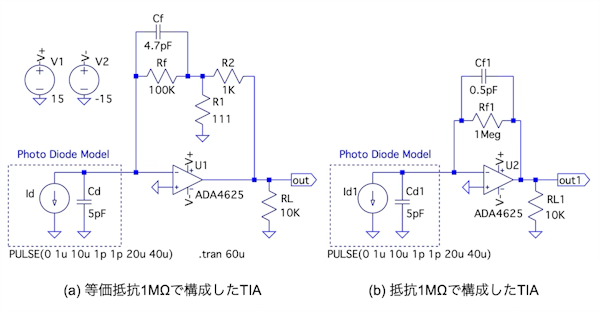
(a) 等価抵抗1MΩで構成したTIA,「C_f=4.7pF」
(b) 抵抗1MΩで構成したTIA,「C_f1=0.5pF」

　図8は図7のシミュレーション結果になります．図7(a)と図7(b)の低周波のゲインは1MΩなので，1μAの電流を1Vに変換しています．そして図7(a)と図7(b)の周波数特性は近くなるようにC_fを4.7pFにしたので，V(out)とV(out1)の出力波形はほぼ同じ時間応答になります．

図8　図7のシミュレーション結果
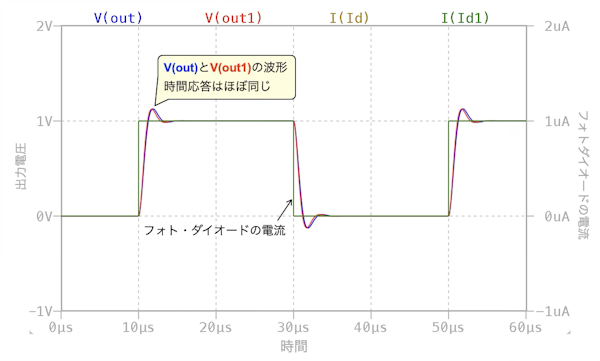
周波数特性が近いので出力波形の時間応答はほぼ同じになる．

　以上，抵抗端子間の容量の影響が低くなる図1(a)のTIAについて解説しました．図1(a)の等価抵抗を使う欠点として雑音が高くなります．そこで，図1(a)を使う場合，出力信号と出力雑音の十分なS/N比の検討も行ってください．

◆参考・引用*文献
(1) ADA4350のデータシート：アナログデバイセズ
(2) ADA4625-1のデータシート：アナログデバイセズ

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice11_040.zip

●データ・ファイル内容
ADA4625 TIA Rf ac.asc：図2の回路
ADA4625 TIA Rf ac.plt：図2のプロットを指定するファイル
ADA4625 TIA T-network ac.asc：図5の回路
ADA4625 TIA T-network ac.plt：図5のプロットを指定するファイル
ADA4625 TIA tran.asc：図7の回路
ADA4625 TIA tran.plt：図7のプロットを指定するファイル