広帯域全波整流回路のOPアンプとひずみの関係

■問題

【 LT1022 】

平賀　公久　Kimihisa Hiraga

　図1は，高速OPアンプ(LT1022)を使った広帯域全波整流回路です．入力信号が正弦波のV₁，outが全波整流出力になります．高速OPアンプのスルーレートは，21V/μsの性能です．
　図1において，V₁の入力振幅が10Vのとき，outの波形がスルーレートにより波形ひずみのない全波整流になるのは，(a)～(d)のどの周波数まででしょうか．

図1　広帯域全波整流回路
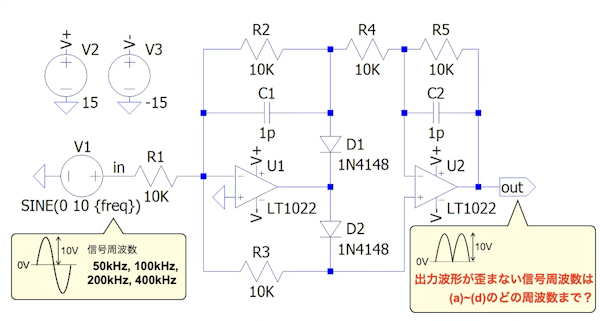
スルーレートにより波形ひずみのない全波整流になる周波数はどこまでか？

(a) 50kHzまで　(b) 100kHzまで　(c) 200kHzまで　(d) 400kHzまで

■ヒント

　OPアンプのスルーレートは「1μsあたりの時間変化でoutの電圧が何V変化する」を表します．スルーレートが21V/μsのとき，振幅10Vの正弦波をひずみがなく通過する周波数の関係を検討すると分かります．

■解答

(c) 200kHzまで

　検討のため，V₁の正弦波の振幅をV_P，周波数をfとします．

V₁の正弦波が「V_in(t)=V_Psin(2πft)」のとき，outの全波整流出力は「V_out(t)=|V_in(t)|」になる
全波整流出力がひずまない周波数のとき，図1の各ノードの振幅はV_in(t)のV_P以内になる
よって，V_in(t)をひずみがなく通過させるスルーレートを検討すれば良い
V_in(t)の時間変化による振幅の最大変化は，V_in(t)を時間微分して「dV_in(t)/dt=2πfV_P」になる
「dV_in(t)/dt」はスルーレートを表すので，信号がひずまない必要なスルーレートは，正弦波の周波数(f)と振幅(V_P)の関数で決まる
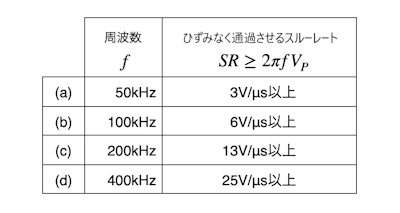
「V_P=10V」のとき，(a)～(d)の周波数をひずみがなく通過させる最小のスルーレートは表1になる
LT1022のスルーレートは，21V/μsなので，表1の200kHzまではひずみがない．400kHzは，スルーレートが不足してひずむ

　この検討より，(c) 200kHzまでが正解になります．

表1　「V_P=10V」の正弦波をひずみがなく通過させるスルーレートと周波数の関係

■解説

●広帯域全波整流回路について
　図1は，LT1022⁽¹⁾のデータシートのP8にある全波整流のアプリケーション回路になります．全波整流回路の出力は，入力の正弦波の正の半波はそのまま出力し，入力の負の半波は位相を反転させて出力します．この動作により，出力波形は正弦波の正の半波が連なる波形になります．図1の回路の特徴として，使用する抵抗(R₁，R₂，R₃，R₄，R₅)は同じ抵抗値で回路を構成できます．また全波整流回路内の各ノードの振幅は，入力の正弦波の振幅以内になります．C₁とC₂は負帰還を安定にする補償コンデンサです．
　全波整流回路を広帯域にするには，OPアンプが高速でなければ動作しません．OPアンプが高速に動作する規格としてスルーレートがあります．OPアンプのスルーレートは「1μsあたりの時間変化でoutの電圧が何V変化する」で規定されます．このスルーレートによって，ひずみがなく回路を通過できる正弦波の振幅と周波数が決まることになります．
　本稿では，先に全波整流回路の動作について解説します．その後，スルーレートと正弦波の振幅と周波数の関係について机上計算します．最後に図1の回路動作をシミュレーションで確かめます．

●全波整流回路の動作
　ここでは，全波整流回路の動作について検討します．解説のためV₁の入力信号の電圧は，V_inとします．図1の全波整流回路は，入力信号が正(V_in＞0)のときOPアンプU₁の出力は負になるので，D₁のダイオードは順方向電圧がかかりONになり，D₂のダイオードは逆方向電圧がかかりOFFになります．逆に入力信号が負(V_in＜0)のとき，OPアンプU₁の出力は正になるので，D₁のダイオードは逆方向電圧がかかりOFFになり，D₂のダイオードは順方向電圧がかかりONになります．このように入力電圧により回路が切り替わるので，入力電圧が正のときと負のときで場合分けして検討します．

▼入力信号が正のときの動作
　図2は，図1の入力信号が正のときの等価回路になります．D₁はONなので回路に示し，D₂がOFFなので回路に示していません．回路の抵抗は同じ抵抗値なので「R₁=R₂=R₃=R₄=R₅=R」としました．

図2　入力信号が正のときの等価回路
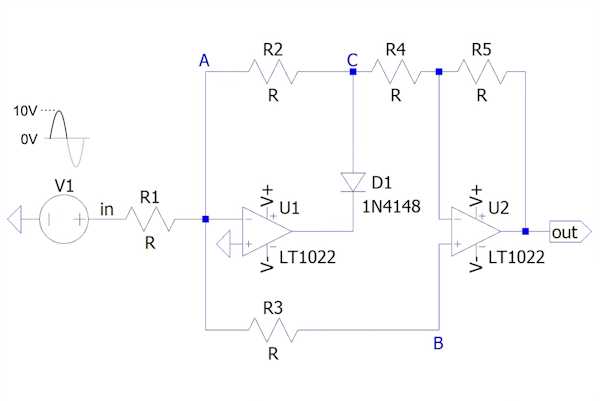
D₁はONなので回路に示し，D₂がOFFなので回路に示していない．

　図2を使いinからoutまでの関係を調べます．図2より回路の状態は次になります．

U₁の負帰還の効果により，Aノードはバーチャル・グラウンドなので，Bノードも同じバーチャル・グラウンドになる
R₁，R₂，U₁はinが入力でCノードが出力になり，ゲインが-1倍の反転アンプとして動作する
R₄，R₅，U₂はCノードが入力でoutが出力になり，ゲインが-1倍の反転アンプとして動作する

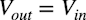　これにより，inからoutまでは，ゲインが-1倍の2つの反転アンプを通過するので，式1の関係になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

▼入力信号が負のときの動作
　図3は，図1の入力信号が負のときの等価回路になります．D₁はOFFなので回路に示さず，D₂がONなので回路に示しています．

図3　入力信号が負のときの等価回路
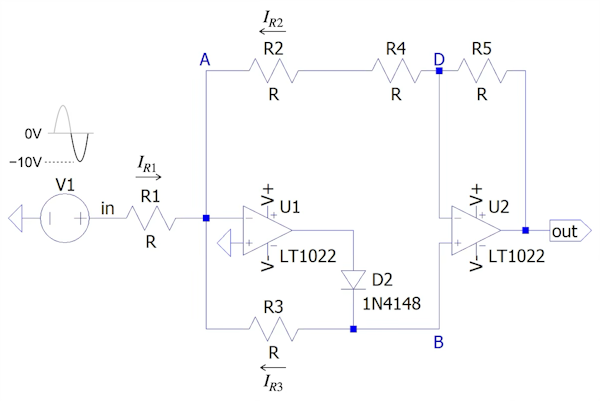
D₁はOFFのため回路に示さず，D₂がONなので回路に示しています．

　図3を使いinからBノードまでの関係を調べます．図3より回路の状態は以下になります．

図3のAノードは，U₁の負帰還によりバーチャル・グラウンドになる
BノードとDノードはU₂の負帰還によりバーチャル・ショートとなり同じ電圧になる
キルヒホッフの電流則より「I_R1+I_R2+I_R3=0」となる
抵抗値は全て同じ「R₁=R₂=R₃=R₄=R₅＝R」なので，Bノードの電圧をV_Bとすると，「I_R1=V_in/R，I_R2=V_B/2R，I_R3=V_B/R」になる

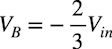これらの状態を使って整理すると，inの電圧とBノードの電圧は式2の関係となります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　次にBノードからoutまでの関係を調べます．Aノードは，バーチャル・グラウンドなので，BノードからoutまではR₂，R₄，R₅，U₂からなる非反転アンプとなり，式3となります．

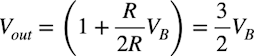・・・・・・・・・・・・・・・・・・・・・・・(3)

　式2と式3より，inからoutまでは式4の関係になります．

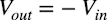・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　これより，入力信号が正(V_in＞0)のときは式1，入力信号が負(V_in＜0)のときは式4となり，outは正側に波形が現れる全波整流回路になります．

●OPアンプのスルーレートを調べる
　シミュレーションで使用するLT1022マクロモデルのスルーレートを調べます．データシートを参照すると，製品のLT1022M，LT1022CH，LT1022CN8のスルーレート規格は最小18V/μs，標準24V/μsです．今回使用するLT1022マクロモデルはこの規格のどの辺りにあるかを調べるのが目的です．
　図4は，LT1022を使ったゲインが-1倍の反転アンプになります．入力のV₁は振幅が±10Vの矩形波になります．このときのoutの波形よりスルーレートを求めます．シミュレーションは「.tran」コマンドを用い，0μs～40μs間の過渡解析になります．

図4　ゲインが-1倍の反転アンプのスルーレートを調べる回路

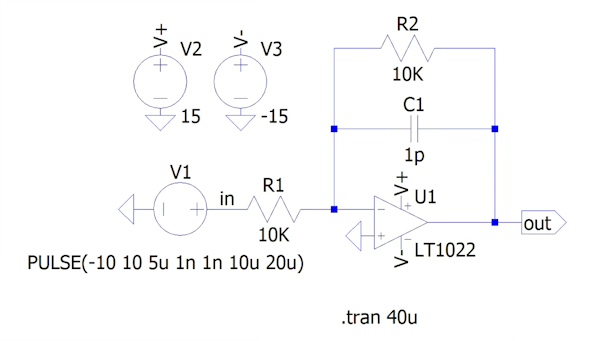
　図5は，図4のシミュレーション結果になります．図5の上段はinのラベルでプロットした入力波形です．図5の中段は，outのラベルでプロットした出力波形です．図5の下段は，outの波形を導関数d()を用いて時間微分したスルーレートの出力波形になります．
　図5の中段のoutの立ち上がりと立ち下がりのスルーレートは，図5の下段より，21V/μsであるのが分かります．このスルーレートを図1の問題文で使用しています．

図5　図4のシミュレーション結果
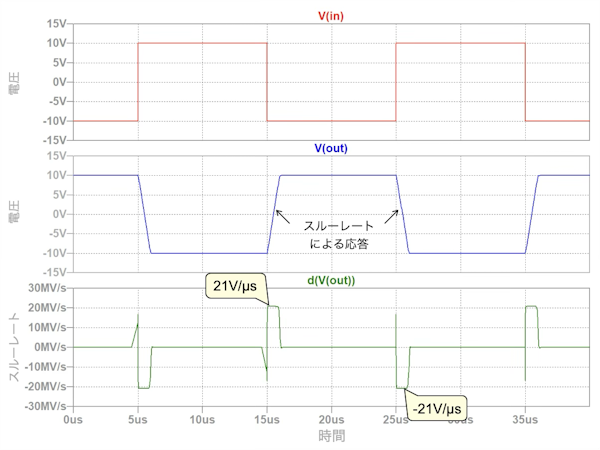
上段は入力の矩形波をプロット
中段はoutの波形をプロット
下段はoutのスルーレートを導関数で計算したプロット

●正弦波をひずみがなく通過させるスルーレート
　次に，正弦波をひずみがなく通過させるスルーレートの関係について，図6を使い机上計算で検討します．図6は「R₁=R₂」とした反転アンプで，ゲインは-1倍になります．

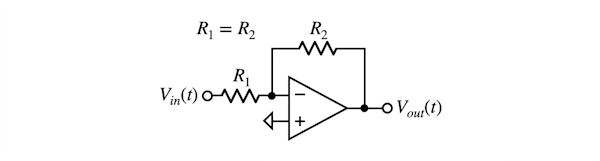
図6　正弦波をひずみがなく通過させるスルーレートを机上計算する回路

　図6の入力になるV_in(t)は，振幅がV_P，周波数をfとした，式5の正弦波とします．

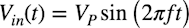・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　V_in(t)の時間変化における振幅の変化を求めると，式5を時間微分して式6になります．

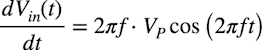・・・・・・・・・・・・・・・・・・・・・・・(6)

　式6のcos関数の最大値は1であること，時間微分はスルーレートを表すことから，正弦波をひずみがなく通過させるスルーレートは式7の関係になります．

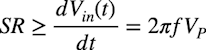・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　この検討を図示すると図7になります．図7(a)はV_in(t)の波形，図7(b)はゲインが-1倍の反転アンプを通過した波形のイメージ図です．

図7　正弦波をひずみがなく通過させるスルーレートのイメージ図

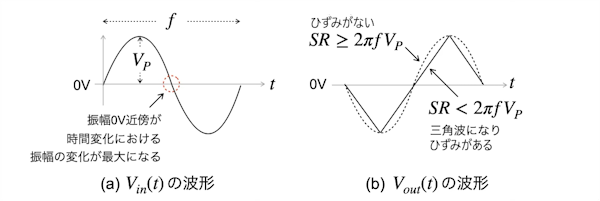
　図7(a)で，正弦波の時間変化における振幅の変化の最大値は，正弦波振幅が0Vと交差する近傍です．これは全波整流回路の振幅0V近傍の変化に相当するので，この検討は全波整流回路にも当てはまります．
　図7(b)で，スルーレート(SR)が「2πfV_P」以上のとき，点線のようにひずみはありません．しかし，スルーレートが「2πfV_P」未満になると，時間変化に対する振幅の変化が追いつかず，実線で示す三角波のようになり，ひずみがあります．このようにOPアンプのスルーレートと，正弦波の振幅V_Pと周波数fの関係により，ひずみがなく通過させるスルーレートが分かります．
　解答で解説したように，正弦波の振幅を10Vとしたとき，正弦波の波形をひずみなく通過させるには式7の関係となり，式7は表1と同じ周波数になります．OPアンプのスルーレートは，21V/μsなので，表1の200kHzまではひずみがなく，400kHzはスルーレートが不足(25V/μs以上)してひずむことになり，(c) 200kHzまでが正解になります．

●全波整流回路のシミュレーション
　図8は，図1の全波整流回路をシミュレーションする回路です．正弦波の振幅が「V_P=10V」のとき，(a)～(d)の周波数(50kHz，100kHz，200kHz，400kHz)でどのような波形になるのかシミュレーションします．
　V₁の周波数は，freqの変数で与え「.step」コマンドで50kHz，100kHz，200kHz，400kHzと変化させています．シミュレーション時間は「.tran」コマンドを用い，0μs～25μs間の過渡解析になります．

図8　図1の回路をシミュレーションする回路
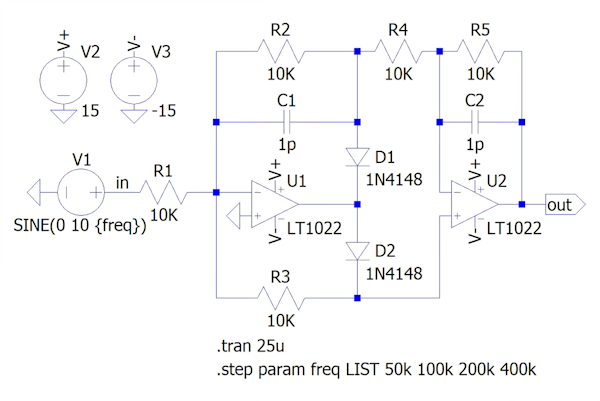
正弦波の振幅が「V_P=10V」で，周波数は，50kHz，100kHz，200kHz，400kHzの4種．

　図9は，図8のシミュレーション結果になります．プロットは4段になり，上から正弦波周波数が50kHz，100kHz，200kHz，400kHzのoutの波形になります．各段には入力の正弦波をinのラベル(赤)でプロット，出力をoutのラベル(青)でプロットしました．

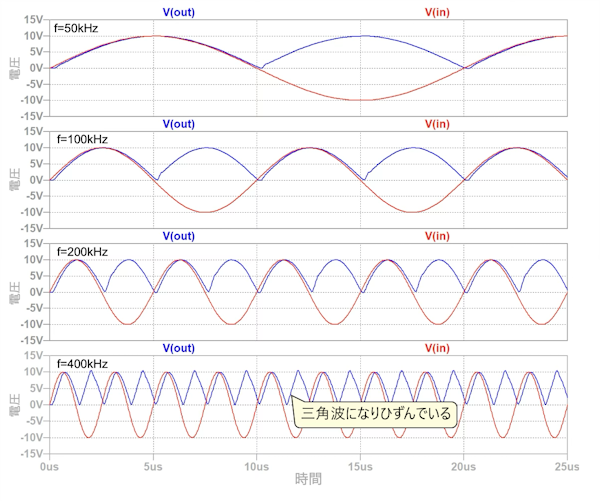
図9　図8のシミュレーション結果 50kHz，100kHz，200kHzでは全波整流回路の出力は入力に追随している．
400kHzはスルーレートで制限を受け，三角波になる．

　図9より周波数が200kHzまではスルーレートが原因となるひずみはありません．しかし，周波数が400kHzになると，outの波形が三角波になりひずむことが分かります．

　以上，広帯域全波整流回路でoutの波形がスルーレートによるひずみを発生しない正弦波振幅(V_P)と周波数(f)についての関係について解説しました．
　OPアンプのスルーレートの規格には，最小値と標準値があります．一方，OPアンプのマクロモデルは一定で，変更できないので最小値になるシミュレーションはできません．OPアンプのスルーレートが最小になった場合の検証が必要な場合は，机上計算で予測できます．

◆参考・引用*文献
(1) LT1022のデータシート：アナログデバイセズ

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice11_036.zip

●データ・ファイル内容
LT1022 SR.asc：図4の回路
LT1022 SR.plt：図4のプロットを指定するファイル
LT1022 Wide Bandwidth Absolute Value Circuit.asc：図8の回路
LT1022 Wide Bandwidth Absolute Value Circuit.plt：図8のプロットを指定するファイル