負帰還アンプで大きな負荷容量を安定に駆動する方法

■問題

【 AD8510 】

平賀　公久　Kimihisa Hiraga

　図1は，OPアンプを使用し，大きな負荷容量(C_L=0.01μF)でも，安定に駆動させるために補償した負帰還アンプです．図1において，OPアンプ内部の出力抵抗が59Ωのとき，負帰還が安定動作するC₁の容量として近いのは(a)～(d)のどれでしょうか．

図1　0.01μFの大きな負荷容量がついた反転アンプ
負帰還を安定にする最適なC₁の容量に近いのは(a)～(d)のどれ？

(a) 1pF　(b) 4.7pF　(c) 22pF　(d) 68pF

■ヒント

　図1の負帰還安定補償は，負帰還回路で生まれる極の周波数(ゲインが低下し位相が遅れ始める)とゼロの周波数(ゲインが増加し位相が進み始める)を同じ周波数にして，ゲインと位相の変化をキャンセルします．
　具体的には負帰還回路を場合分けし,「高周波でC₁はショートとみなし，R_X＜＜R₂，R_o＜＜R₁の条件」のときの極をf_P1，ゼロをf_Z1とします．
　次に「負荷容量(C_L)はオープンのとき」の極をf_P2，ゼロをf_Z2とします．2つの極とゼロの周波数を「f_P1=f_Z2，f_P2=f_Z1」にすることで補償します．図1のR_Xはこの条件で最適化した値を使いています．
　そして残りのC₁を検討します．

■解答

(d) 68pF

　図1は，負帰還回路を場合分けし，ヒントに示した2つの極とゼロの周波数を「f_P1=f_Z2，f_P2=f_Z1」にすることによりR_XとC₁の2つを適切な値にして補償します．図1のR_Xは最適にした抵抗値を使用しているため,「f_P1=f_Z2，f_P2=f_Z1」のどちらかの条件でC₁を検討することになります．ここでは「f_P1=f_Z2」の条件からC₁を検討します．

「高周波でC₁はショートとみなし，R_X＜＜R₂，R_o＜＜R₁の条件」のとき,「R_o=59Ω，R_X=6.2Ω」より，極は「f_P1=1/(2πC_L (R_o+R_X))=243kHz」になります
f_Z2は,「f_Z2=1/(2πC₁ (R_X+R₂))」になります
前述のf_Z2の式を使い「f_Z2=243kHz」にして「R_X=6.2Ω」と「R₂=10kΩ」の値を使いC₁を求めると,「C₁=65pF」になります
(a)～(d)の中で近いのは「C₁=68pF」になります

　これよりより，(d)が正解になります．

■解説

●負荷容量により負帰還は不安定になる
　終端が適切でない同軸ケーブルやノイズを除去する大きなコンデンサ等を駆動するとき，負帰還アンプは，不安定になり，リンギングや発振などの悪い影響が出てきます．
　不安定になるのは，大きな負荷容量による位相の遅れが原因です．このため負帰還側で不安定にならないような対策が必要になります．図1で使用したAD8510⁽¹⁾はゲインが1倍で負荷容量1000pFまで安定に動作するのが特徴ですが，それより大きな負荷容量では不安定になります．

●フィードバック内補償を使う
　図1の補償方法は参考文献(2)によると「フィードバック内補償」と呼ばれています．これは補償するC₁とR_Xが負帰還ループの内側にあることによります．
　フィードバック内補償の利点として，R_Xを加えても負帰還ループ内にあるので，直流精度への影響は低くなります．ただし，出力振幅とスルーレートが低くならないように，R_Xは低い抵抗値にする必要があります．フィードバック内補償の検討にはOPアンプ内部の出力抵抗値も必要になります．
　本稿では，まず大きな負帰還容量があるとき，補償前の回路では時間応答と負帰還ループの周波数特性が悪化するのを確認します．次にOPアンプ内部の出力抵抗を調べ，その後にフィードバック内補償について解説します．最後に補償後の効果をシミュレーションで確認します．

●補償前の回路の時間応答
　図2は，図1の補償前の負帰還アンプで，ゲインが10倍の反転アンプです．図1と同じ大きな負荷容量(C_L=0.01μF)をoutに接続しています．OPアンプは，参考文献(2)で使用しているAD8510⁽¹⁾を使いました．

図2　補償が無い負帰還アンプの時間応答を調べる回路
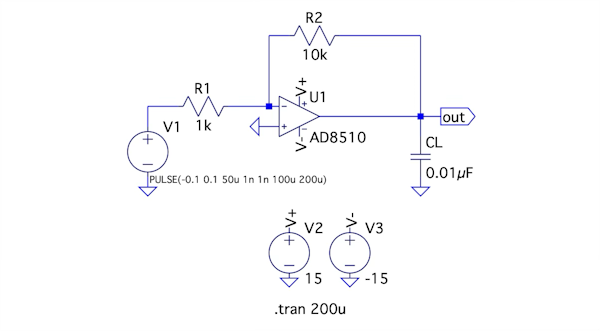
outに負荷容量0.01μFを接続している．

　図2の回路でV₁から振幅の最大が±0.1Vの矩形波を入力し，補償前の回路の時間応答をシミュレーションで調べます．シミュレーションは「.tran」コマンドを使い，200μsまでの過渡解析になります．
　図3は，図2のシミュレーション結果になります．ゲインが10倍の反転アンプなので，振幅の最大は±1Vで位相は反転します．図3のプロットで，矩形波の立ち上がりと立ち下がりにリンギングが発生しています．これが負荷容量による影響になります．

図3　図2のシミュレーション結果
outの立ち上がりと立ち下がりでリンギングが発生．

　次に補償前の負帰還アンプでループ・ゲインと位相の関係を図4の回路で調べます．図4はループ・ゲインと位相を評価する回路で，LTspiceのEducationalフォルダにある「LoogGain2.asc」を編集して使用しています．この評価回路はMiddle Brook法と呼ばれるもので，正確なループ・ゲインと位相の評価ができます．ループ・ゲインと位相は次の計算式でプロットします．

プロットで使う計算式：((I(V3)/I(V4))*(-V(x)/V(y))-1)/((I(V3)/I(V4))+(-V(x)/V(y))+2)

　シミュレーションは「.ac」コマンドを使い，周波数が1Hzから10MHz間を周波数が10倍あたり30ポイントのスイープになります．

図4　補償が無い負帰還アンプのループ・ゲインと位相を調べる回路
Middle Brook法を使用する．

　図5は，図4のシミュレーション結果になります．

図5　図4のシミュレーション結果
位相余裕は27°しかなく負帰還は不安定．

　1Hzからおよそ10kHz間はOPアンプの周波数特性になります．それ以上の周波数では負荷容量による位相遅れが発生し，位相余裕が27°になります．一般的に負帰還が安定に動作する位相余裕は60°が目安なので，負帰還は不安定になっているのが分かります．

●OPアンプ内部の出力抵抗を調べる
　ここでは，OPアンプ内部の出力抵抗を求めるため，OPアンプのオープン・ループ・ゲインと，ユニティ・ゲイン・バッファの出力インピーダンスをシミュレーションで調べ，その2つの値から計算で求めます．
　図6は，OPアンプ(AD8510)のオープン・ループ・ゲインを図4と同じMiddle Brook法で調べる回路になります．シミュレーションの設定は図4と同じです．

図6　OPアンプのオープン・ループ・ゲインを調べる回路
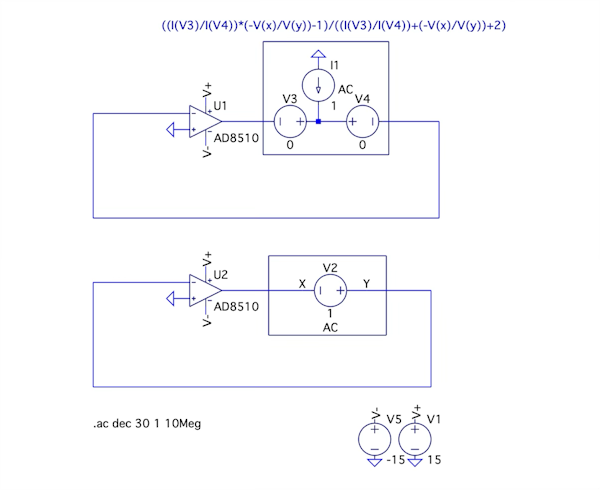
OPアンプの出力抵抗を求めるため，1Hzでのオープン・ループ・ゲインを調べる．

　図7は，図6のシミュレーション結果になります．Y軸はデシベルからログスケールに変更してゲインを倍率で表しています．1HzでのOPアンプのオープン・ループ・ゲインを調べると230718倍になります．

図7　図6のシミュレーション結果
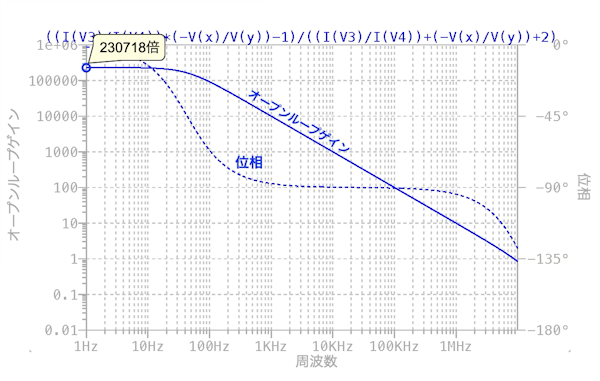
1Hzでのゲインは230718倍．

　図8は，OPアンプ(AD8510)を使ったユニティ・ゲイン・バッファの出力インピーダンス周波数特性を調べる回路になります．ユニティ・ゲイン・バッファの出力にテスト信号源としてI₁の交流信号源を加えました．

図8　ユニティ・ゲイン・バッファで負帰還をかけたとき，1Hzでの出力インピーダンスを調べる回路
調べた出力インピーダンスとオープン・ループ・ゲインより，OPアンプ内部の出力抵抗を計算する．

　「.ac」コマンドは図4と同じです．ユニティ・ゲイン・バッファの出力インピーダンスは，負帰還の効果でOPアンプ内部の出力抵抗をオープン・ループ・ゲインで割った値になります．
　図9は，図8のシミュレーション結果になります．図9のY軸は，I₁の交流電流変化に対するoutの交流電圧変化の周波数特性です．これよりY軸は出力インピーダンスを表しています．図9より，1Hzでの出力インピーダンスは257μΩになるのが分かります．

図9　図7のシミュレーション結果
ユニティ・ゲイン・バッファの1Hzでの出力インピーダンスは257μΩ．

　OPアンプ内部の出力抵抗は，ユニティ・ゲイン・バッファの出力インピーダンスにオープン・ループ・ゲインを掛けた値になります．図7と図9で調べた1Hzの2つの値を使うと，AD8510の内部の出力抵抗(R_o)は式1の59Ωであるのが分かります．

・・・・・・・・・・・・・・・・・・・・・・(1)

　図1にはOPアンプ内部の出力抵抗として，式1の値を記載しています．

●フィードバック内補償の検討
　ここではフィードバック内補償の検討をするため，図1を書き直した図10を使います．v_Aの信号は負帰還回路を通りv_BでOPアンプに負帰還されます．

図10　図1の負帰還アンプを書き直した回路

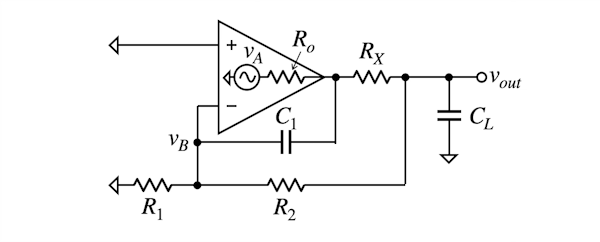
　図10の負帰還部分を抜き出したのが図11(a)になります．フィードバック内補償は，図11(a)の負帰還回路を場合分けし，図11(b)の「高周波でC₁がショートとみなし，R_X＜＜R₂，R_o＜＜R₁の条件」のときのv_Aからv_Bまでの伝達特性の極をf_P1，ゼロをf_Z1とします．　次に図11(c)の「負荷容量(C_L)がオープンのとき」のv_Aからv_Bまでの伝達特性の極をf_P2，ゼロをf_Z2とします．極はゲインが低下し位相が遅れ始めるところ，ゼロはゲインが増加し位相が進み始めるところです．2つの極とゼロの周波数を「f_P1=f_Z2，f_P2=f_Z1」にすることでゲインと位相の変化をキャンセルする補償方法になります．

図11　補償方法について解説する3つの図
(a)図10の負帰還を抜き出した回路
(b)図11(a)のC₁をショート，R_X＜＜R₂，R_o＜＜R₁とした回路
(c)図11(a)のC_Lをオープンとした回路

●フィードバック内補償の机上計算
　図11(b)と図11(c)を使って，フィードバック内補償するときのR_XとC₁の値を机上計算で求めます．v_Aからv_Bまでの伝達関数を検討すると，図11(b)の極は式2になります．

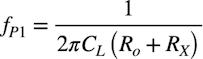・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　そして図11(b)のゼロは式3になります．

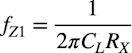・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　同様に図11(c)の極は式4になります．

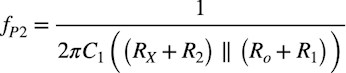・・・・・・・・・・・・・・・・・・・(4)

　そして図11(c)のゼロは式5になります．

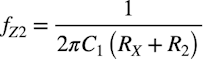・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式2と式5を使って「f_P1=f_Z2」，そして式3と式4を使って「f_P2=f_Z1」とします．この2つの関係と「R_X＜＜R₂，R_o＜＜R₁」の条件を使い，近似より，R_Xは式6になります．具体的な抵抗値は「R_o=59Ω，R₁=1kΩ，R₂=10kΩ」より，式6は「R_X=5.9Ω」となります．この結果に近く，E24系列で選びやすい抵抗として，ここでは「R_X=6.2Ω」としました．この値が図1のR_Xになっています．

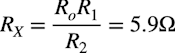・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　同様に「f_P1=f_Z2，f_P2=f_Z1」とすると，C₁は式7になります．C₁の選びやすい値として，ここでは「C₁=68pF」としました．これより解答の(d)になるのが分かります．

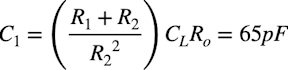・・・・・・・・・・・・・・・・・・・・・・・(7)

　これらの選びやすい抵抗の「R_X=6.2Ω」と「C₁=68pF」を使い，f_P1，f_Z1，f_P2，f_Z2を計算すると，「f_P1=243kHz」，「f_Z1=2.6MHz」，「f_P2=2.5MHz」，「f_Z1=234kHz」となり，およそ「f_P1=f_Z2，f_P2=f_Z1」になるのが分かります．
　参考文献(2)では，C₁を求める式7に「1+R₂/R₁」の項を含んだ式8になっています．これは実験などの検証により加えられた項になります．式8を使うと，C₁は71pFになります．

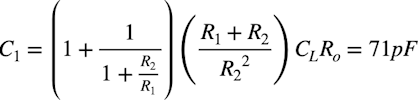・・・・・・・・・・・・・・(8)

●補償後の負帰還ループのゲインと位相変化の確認
　図12は，図1のC₁を68pFとした補償後の負帰還ループのゲインと位相の変化を確認する回路になります．シミュレーションの設定は図4と同じです．

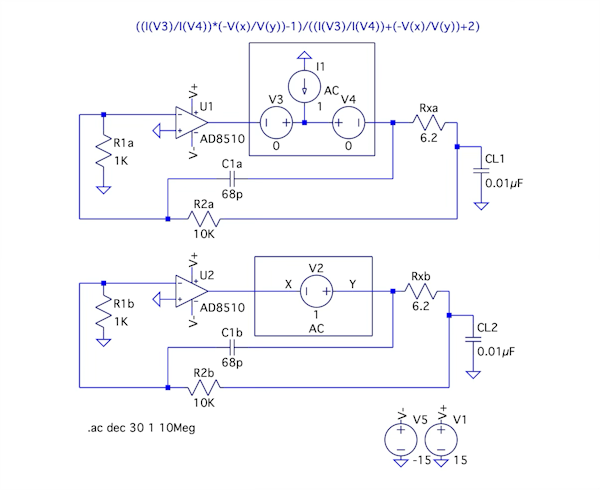
図12　図1のフィードバック内補償をしたループ・ゲインと位相を調べる回路
図1のC₁に相当するC_1aとC_1bは68pFにしている．

　図13は図12のシミュレーション結果になります．補償後の位相余裕は80°になり負帰還は安定しています．補償前の図5のプロットと比べると，10kHz以上で見られたゲインの低下と位相の遅れはキャンセルされているのが分かります．

図13　図12のシミュレーション結果
位相余裕は安定して80°になる．

●補償後の時間応答の確認
　図14は，補償後の回路で図1のC₁を68pFとした回路になります．図14を使って時間応答の確認をします．シミュレーションの設定は図2と同じになります．

図14　図1の時間応答を調べる回路
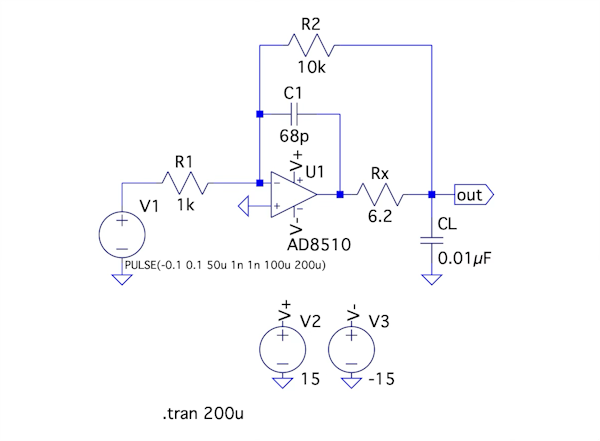
C₁は68pFにしている．

　図15は，図14のシミュレーション結果になります．図3の補償前のプロットと比べると，矩形波の立ち上がりと立ち下がりのリンギングはなくなり，回路が安定していることが分かります．

図15　図14のシミュレーション結果
補償後はリンギングがない．

　以上，大きな負荷容量を駆動するときの補償について解説しました．この補償方法は電圧帰還型OPアンプ全般で使えるものになります．シミュレーションで動作を確認した後は，実機での確認も忘れずに行ってください．

◆参考・引用*文献
(1) AD8510のデータシート：アナログデバイセズ
(2) アプリケーション・エンジニアに尋ねる ― 32容量性負荷によって損なわれるオペアンプ回路の安定性，この問題にはどう対処すればよいのか？：アナログデバイセズ

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice11_026.zip

●データ・ファイル内容
INV_Amp tran.asc：図2の回路
INV_Amp tran.plt：図2のプロットを指定するファイル
LoopGain.asc：図4の回路
LoopGain.plt：図4のプロットを指定するファイル
OpenLoopGain.asc：図6の回路
OpenLoopGain.plt：図6のプロットを指定するファイル
Output Resistance.asc：図8の回路
Output Resistance.plt：図8のプロットを指定するファイル
LoopGain Compensation.asc：図12の回路
LoopGain Compensation.plt：図12のプロットを指定するファイル
INV_Amp_Compensation tran.asc：図14の回路
INV_Amp_Compensation tran.plt：図14のプロットを指定するファイル