多重帰還型バンド・パス・フィルタの設計方法

LTspice メール・マガジン全アーカイブs

■問題

【 LTC6258 / LTC6992-1 】

平賀　公久　Kimihisa Hiraga

　図1は，低消費電流の入出力レール・ツー・レールOPアンプ（LTC6258）を使った，正弦波発振器などに使用される，多重帰還型バンド・パス・フィルタです．図1のフィルタ回路の特徴として(a)～(d)の中で正しい説明はどれでしょうか．

図1　入出力レール・ツー・レールOPアンプを使った多重帰還型バンド・パス・フィルタ
LTC6258データシートの低消費電力の方形波-正弦波発振器内で使っている．

(a) 中心周波数はR₁とR₂とC₁とC₂で決まる
(b) C₁/C₂でフィルタのQが決まる
(c) outの直流電圧は0Vになる
(d) R₁とR₃でゲインの調整をしている

■ヒント

　多重帰還型バンド・パス・フィルタの中心周波数とQはどの素子で決まるか，そのときのゲインはどうなるのか，outの直流電圧は回路のどこで決まるかを検討すると分かります．Qは，フィルタのパラメータの1つで，Quality factorの略語です．

■解答

(d) R₁とR₃でゲインの調整をしている

　図1の多重帰還型バンド・パス・フィルタの特徴を次に示します．

中心周波数は「R₁||R₃」の並列抵抗とR₂とC₁とC₂で決まる
フィルタのQはR₂/R₁の比に関係する
OPアンプはC₁とC₂で直流カットされるので，outの直流電圧はOPアンプの非反転端子の電圧で決まり，図1では2.5Vになる
R₁とR₃の分圧回路でゲイン調整している

　これより，(d)が正解になります．

■解説

●多重帰還型バンド・パス・フィルタについて
　図1の多重帰還型バンド・パス・フィルタは「R₁=1，ω₀=1，Q=3.14」と設定し正規化します．「Q=3.14」と正規化された回路に設定され，フィルタの周波数特性が固定され，中心周波数が決まります．
　また，多重帰還型バンド・パス・フィルタは，C₁とC₂で直流カットするため，フィルタの直流バイアス電圧は，OPアンプの非反転端子に加える電圧になります．これより，前段の回路との接続で直流電圧の整合をとる必要がないことから接続が簡単になります．以降では多重帰還型バンド・パス・フィルタの設計の流れを解説します．

●多重帰還型バンド・パス・フィルタの基本形
　図2は，多重帰還型バンド・パス・フィルタの基本形になります．図1との違いは，図2にはR₃がありません．R₁，R₂とC₁，C₂の値は，「R₁=1Ω，ω₀=1，Q=3.14」として正規化した回路定数になります．ここでは，図2の正規化した回路定数の求め方から始めます．ただし，C₁とC₂は同じ値のコンデンサを使うこととし，計算では「C₁=C₂=C」とします．

図2　多重帰還型バンド・パス・フィルタ回路
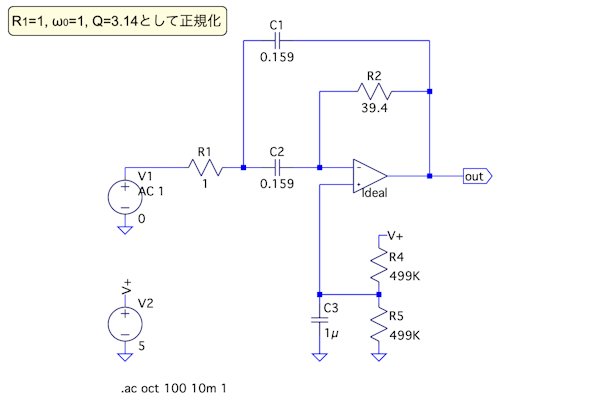
ゲインが120dBの理想OPアンプを使用．
「R₁=1Ω，ω₀=1，Q=3.14」で正規化している．

　図2のV₁からoutまでの伝達関数は式1になります．この伝達関数の求め方は「特定の周波数だけを通過させるフィルタ」にも詳しい解説があります．

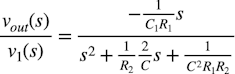・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　バンド・パス・フィルタの一般式は式2になり，式1と式2の各項を比較することにより，中心周波数（ω₀）とQが分かります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　具体的には，中心周波数は式3になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　Qは式4になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式3と式4を使い，「R₁=1Ω，ω₀=1，Q=3.14」で正規化します．まず式4に「R₁=1Ω」を入れると式5の関係になります．式5へ「Q=3.14」を入れると，「R₂=39.4Ω」になり，図2の値になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式3へ「R₁=1Ω，R₂=39.4Ω」を入れると式6の関係になります．式6へ「Q=3.14」を入れると，「C=0.159F」になり，図2の値になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　次に式2のバンド・パス・フィルタの一般式のゲインを使い，式2と式1の比較より式1のゲインを求めます．式2のバンド・パス・フィルタの一般式で，中心周波数「ω₀=1」のときの伝達関数は式7になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式7の絶対値をとるとゲインになり，式8になります．式8よりゲインは1倍になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　一方，式1の多重帰還型バンド・パス・フィルタの伝達関数に「R₁=1Ω，R₂=39.4Ω，C=0.159F」を入れると式9になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　式7のゲインが式8なので，式9のゲインは式10になります．具体的には，式10へ「Q=3.14」を入れると，ゲイン(H)は「H=25.89dB」になります．ここで，Hは実装したフィルタのゲインです．

・・・・・・・・・・・・・・・・・・・・・・・・・(10)

●多重帰還型バンド・パス・フィルタ基本
　図3は，図2をシミュレーションした結果になります．中心周波数は正規化した「ω₀=1 (159mHz)」になります．Qは中心周波数と-3dBになる帯域より計算でき，「Q=3.13」になります．ゲインは式10で計算した「H=25.89dB」になります．この結果より，正規化した通りの周波数特性になるのが分かります．

図3　図2のシミュレーション結果
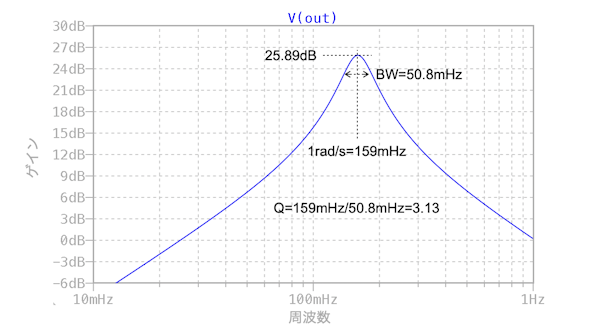
中心周波数は1rad/s(159mHz)，Qが3.13，ゲインが25.89dB．

●ゲインを0dBに調整する
　図2の多重帰還型バンド・パス・フィルタの基本形は，ゲインが高くなります．このゲインを低くする調整として図1のR₃を使います．図1のR₁とR₃は分圧回路になり，バンド・パス・フィルタのゲインを低くできます．図4は，図1のR₁とR₃の分圧回路を抜き出しました．この回路を使って，バンド・パス・フィルタの中心周波数とQを変えずに，ゲインを0dBにする解説をします．

図4　バンド・パス・フィルタのゲインを0dBにする抵抗分圧回路
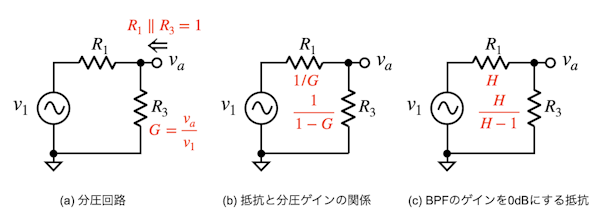
(a)分圧回路，(b)抵抗値と分圧ゲインの関係，(c) BPFをゲインを0dBにする抵抗値．

　ゲインを調整する分圧回路に求められる要件は，図4(a)において分圧のvaから分圧回路側を見た抵抗が，図2のR₁と等しくならなければ，フィルタの特性が変化します．これより，式11のようにR₁とR₃の並列抵抗が1Ωになるようにします．

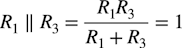・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　図4(a)の分圧回路のゲインは式12になります．分圧回路のR₁とR₃とゲインの関係を導きます．式11のR₁R₃/(R₁+R₃)を式12のゲインで割ると「R₁=1/G」になります．このR₁を式12に入れると「R₃=1/(1-G)」になります．ここで検討した抵抗と分圧ゲインの関係を図4(b)に示します．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)

　図2の多重帰還型バンド・パス・フィルタのゲイン(H)を抵抗分圧で減衰させてゲインを0dBにするには，式13の関係になります．式13を使うと，図4(b)の「R₁=1/G」は図4(c)の「R₁=H」になります．同様に，図4(b)の「R₃=1/(1-G)」は図4(c)の「R₃=H/(H-1)」になります．

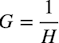・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)

　具体的に，図2のゲインは，式10なので，図4(c)の「R₁=H」の関係より式14になり，「Q=3.14」を入れると19.7Ωになります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)

　そして，図4(c)の「R₃=H/(H-1)」の関係より式15になり，「Q=3.14」を入れると1.05Ωになります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)

●ゲインを0dBにした正規化回路
　図5が図2の正規化回路のゲインを0dBにするR₁とR₃になります．

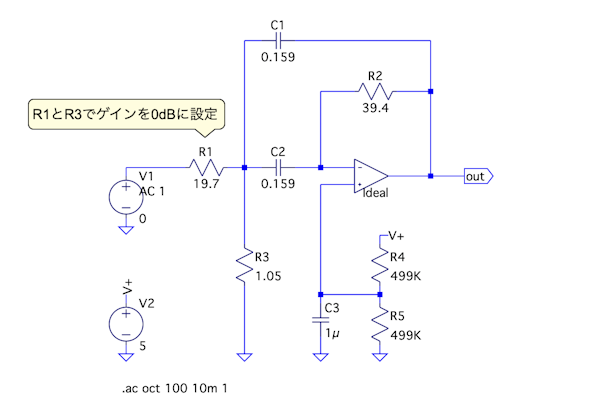
図5　図4の結果を使った多重帰還型バンド・パス・フィルタの正規化回路

　図6は，図5のシミュレーション結果です．このように中心周波数は「ω₀=1(159mHz)，Q=3.13」は変わらずに，ゲインは0dBになるのが確認できます．

図6　図5のシミュレーション結果
中心周波数は1rad/s(159mHz)，Qは3.13，ゲインは0dB．

●抵抗とコンデンサの値の調整
　コンデンサは，選べる値が抵抗より少ないので，先に使うコンデンサの値を決めます．ここでは「C=C₁=C₂=4.7nF」にします．このコンデンサを使い，図5の正規化した回路を，中心周波数f₀は「f₀=10kHz」，フィルタのQは「Q=3.14」，ゲインは「H=0dB」になるように抵抗をスケーリングします．スケーリングした結果は，図7になります．このスケーリングについて解説します．

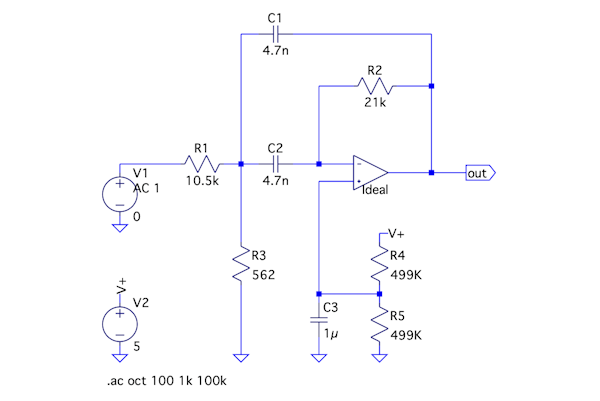
図7　中心周波数を10kHz，Q=3.14，ゲインは0dbへ抵抗とコンデンサをスケーリングした回路

　フィルタ回路のコンデンサのスケーリングは式16を使います．C_newはスケーリング後の値，C_oldはスケーリング前の値，kmはインピーダンス・スケーリング係数，kfは周波数スケーリング係数です．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)

　抵抗のスケーリングは式17を使います．Rnewがスケーリングの値，Roldがスケーリング前の値，kmがインピーダンス・スケーリング係数です．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)

　具体的なスケーリングに入ります．中心周波数を「ω₀=1」から「f₀=10kHz」にするので，周波数スケーリング係数kfは式18になります．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(18)

　スケーリング前のコンデンサは，図5より「C_old=0.159F」，スケーリング後のコンデンサは「C_new=4.7nF」です．式16に式18のkf，スケーリング前のC_old，スケーリング後のC_newを入れると，式19のインピーダンス・スケーリング係数kmが求まります．

・・・・・・・・・・・・・・・・・・・・・・(19)

　式17を使って抵抗を求めると，「R_1new=538*19.7=10.6kΩ，R_2new=538*39.4=21.2kΩ，R_3new=538*1.05=565Ω」になります．この3つの抵抗に近い選びやすい抵抗として，図7の「R₁=10.5kΩ，R₂=21kΩ，R₃=562Ω」になります．

●スケーリング後のフィルタ特性
　図8は，図7のシミュレーション結果になります．中心周波数f₀は「f₀=10.1kHz，Q=3.13，ゲイン(H)=0dB」になり，目標としたフィルタ特性になります．

図8　図7のシミュレーション結果
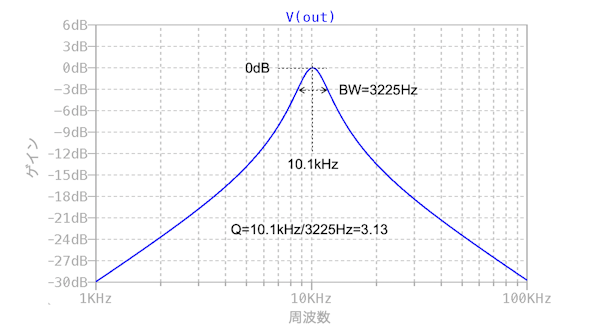
中心周波数は10.1kHz，Qは3.13，ゲインは0dB．

●実際のOPアンプに変更したときのフィルタ特性
　図9は，図7の理想OPアンプをLTC6258へ変更した多重帰還型バンド・パス・フィルタで図1と同じ回路になります．ここでは図9をシミュレーションしてフィルタ特性を確認します．

図9　理想OPアンプからLTC6258へ変更した回路

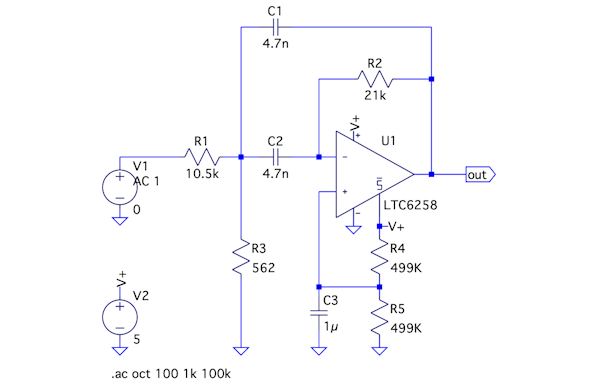
　図10は，図9のシミュレーション結果になります．OPアンプの影響により，中心周波数は9.7kHz，Qは4.7，ゲインは3.3dBと少し差が出てきます．このように最初から実際のOPアンプを使ってシミュレーションすると，OPアンプの影響も加わったものになり混乱が生じます．OPアンプを使ったフィルタの設計は，理想OPアンプで確かめてから実際のOPアンプを使った方が早く作業が進むと思います．

図10　図9のシミュレーション結果
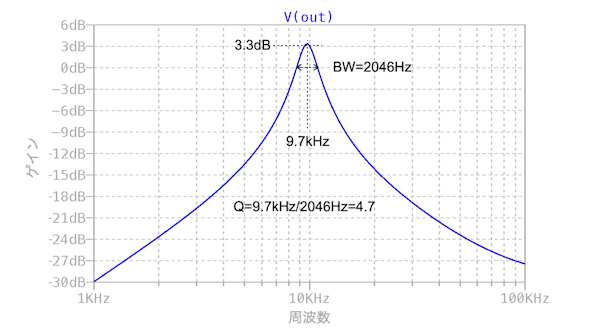
OPアンプの影響によりゲインとQが変わる．
中心周波数が9.7kHz，Qが4.7，ゲインが3.3dB．

●多重帰還型バンド・パス・フィルタの使用例
　図11は，LTC6258のデータシートにある低消費電力の方形波-正弦波発振器になります．LTC6992-1は電圧制御パルス幅変調器で，図11では周波数が10kHzの方形波を出力します．LTC6992-1の出力からR6とC4のロー・パス・フィルタを通り，今回解説した，多重帰還型バンド・パス・フィルタで，フィルタリングして，outから10kHzの正弦波を出力する回路になります．

図11　低消費電力の方形波-正弦波発振器⁽¹⁾

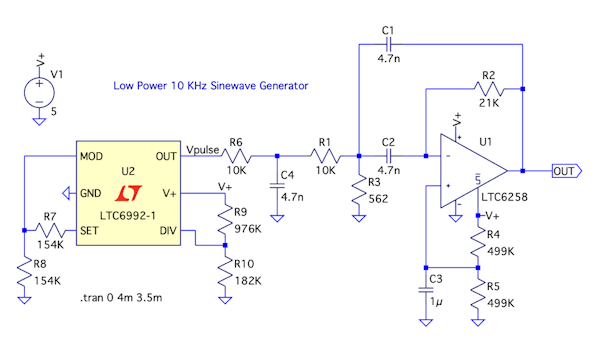
　図12は，図11のシミュレーション結果になります．上段がLTC6992-1の出力で10kHzの矩形波になります．下段は多重帰還型バンド・パス・フィルタの出力で，フィルタリングした後の波形は正弦波になるのが分かります．

図12　図11のシミュレーション結果
上段はLTC6992-1の矩形波出力．下段は多重帰還型バンド・パス・フィルタを通過した正弦波．

　以上，多重帰還型バンド・パス・フィルタの設計方法を解説しました．多重帰還型バンド・パス・フィルタはC₁とC₂で直流カットをするので，縦続接続しやすいフィルタ回路です．そしてQを使って正規化すると，フィルタの設計が楽になります．

◆参考・引用*文献
(1)アナログデバイセズ：LTC6258のデータシート(P16の低消費電力の方形波-正弦波発振器回路)
(2)アナログフィルタの設計：M.E.VAN VALKENBURG，柳沢健監訳・金井元他訳

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice10_036.zip

●データ・ファイル内容
BPF normalize.asc：図2の回路
BPF normalize.plt：図2のプロットを指定するファイル
BPF normalize 0dB.asc：図5の回路
BPF normalize 0dB.plt：図5のプロットを指定するファイル
BPF 10kHz 4700pF Q_3.asc：図7の回路
BPF 10kHz 4700pF Q_3.plt：図7のプロットを指定するファイル
BPF 10kHz 4700pF Q_3 LTC6258.asc：図9の回路
BPF 10kHz 4700pF Q_3 LTC6258.plt：図9のプロットを指定するファイル
Low Power 10 KHz Sinewave Generator.asc：図11の回路
Low Power 10 KHz Sinewave Generator.plt：図11のプロットを指定するファイル
Ideal_OP.asc：ゲインが120dBの理想OPアンプ
Ideal_OP.asy：理想OPアンプのシンボル