電圧ドロップと消費電力を小さくできる整流回路

■問題

【 LT1430 】

小川　敦　Atsushi Ogawa

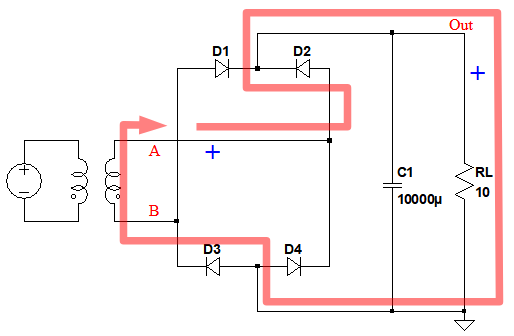
　図1は，ダイオード・ブリッジ(D₁～D₄)を使用した整流回路です．50Hz,100V_RMSの交流電源をトランスの1次側に入力し，Out端子に直流電圧を出力します．トランスの2次側A,B間の電圧は20V_PPとなっています．Out端子とGND間のピーク・ツー・ピーク電圧として近いのは，(a)～(d)のどれでしょうか．ただし，ダイオードの順方向電圧(V_F)は1Vとします．

図1　ダイオード・ブリッジ(D₁～D₄)を使用した電源回路
Out端子とGND間の電圧は？

(a) 18V_PP　(b) 16V_PP　(c) 9V_PP　(d) 8V_PP

■ヒント

　負荷抵抗(R_L)に流れる電流が，どのような経路で流れるかを考えれば，答えは簡単に分かります．

■解答

(d) 8V_PP

　A-B間の電圧が正のとき，電流はD₂を経由してR_Lに流れ，さらにD₃を経由してトランスの2次巻き線に戻ります．また，A-B間の電圧が負のときは，電流はD₁を経由してR_Lに流れ，D₄を経由してトランスの2次巻き線に戻ります．
　どちらもダイオード2個を経由するため，R_Lに加わる電圧は，A-B間の電圧よりも，ダイオードの順方向電圧2個分小さくなります．そのため，Out端子のピーク電圧はA-B間のピーク電圧から2*V_F引いたものとなり，20/2-2=8V_PPとなります．

■解説

●ダイオード・ブリッジ整流回路の動作
　日本の家庭用コンセントから得られるのは，交流100V_RMSの電源です．そのままでは電圧が高く，また交流のままでは使用しにくいため，トランスで電圧を下げ，整流回路で直流にして使用します．図1は整流回路にダイオードを4個使用したもので，図1のように接続したダイオードをダイオード・ブリッジと呼んでいます．ダイオード・ブリッジを使用すると，交流信号を全波整流することができます．
　図2は，A-B間の電圧が正(Aが+)のときの電流ルートを表しています．トランスの2次巻き線A点からの電流はD₂を経由してR_Lに流れ，D₃を経由してトランスの2次巻き線に戻ります．このとき，Out端子の電圧は正の電圧になります．このように，ダイオードを2個経由して負荷に電流が流れるため，負荷抵抗(R_L)に加わる電圧は，A-B間の電圧よりも，ダイオードの順方向電圧2個分小さくなります．

図2　A-B間の電圧が正(Aが+)のときの電流ルート
ダイオードを2個経由して負荷に電流が流れる．

　図3は，A-B間の電圧が負(Bが+)のときの電流ルートです．トランスの2次巻き線B点からの電流はD₁を経由してR_Lに流れ，D₄を経由してトランスの2次巻き線に戻ります．

図3　A-B間の電圧が負(Bが+)のときの電流ルート
ダイオードを2個経由して負荷に電流が流れる．

　この場合も，Out端子の電圧は正の電圧になり，負荷抵抗(R_L)に加わる電圧は，A-B間の電圧よりも，ダイオードの順方向電圧2個分小さくなります．
　このように，A-B間の電圧が正のときも負のときも，Out端子の電圧は正となり，その電圧は，A-B間の電圧から，ダイオードの順方向電圧(V_F)2個分を引いたものになります．Out端子のピーク電圧(V_Out)は，A-B間のピーク・ツー・ピーク電圧をV_ABPPとすると，式1で計算することができ，図1の定数を代入すると，8Vになります．

・・・・・・・・・・・・・・・・・・・・・(1)

●ダイオード・ブリッジ整流回路の確認
　図4は，図1のダイオード・ブリッジ整流回路をシミュレーションする回路です．「.meas」コマンドで負荷抵抗とダイオードの消費電力の平均値を計算しています．

図4　ダイオード・ブリッジ整流回路をシミュレーションする回路
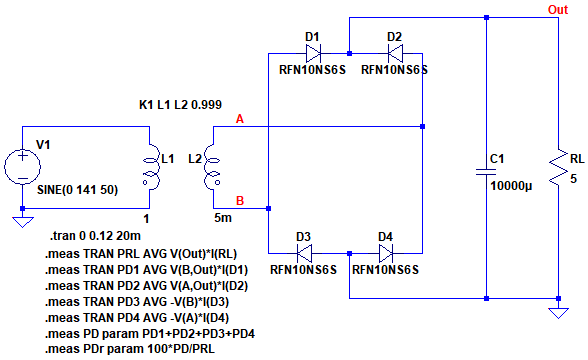
「.meas」コマンドで負荷抵抗とダイオードの消費電力の平均値を計算している．

　図5が図4のシミュレーション結果です．上段がA-B間の電圧とOut端子の電圧です．Out端子のピーク電圧はA-B間のピーク電圧よりも2V低い，8Vとなっています．下段が，負荷抵抗とダイオードの消費電力です．ダイオードは瞬間的にかなり大きな電力を消費していることが分かります．

図5　イオード・ブリッジ整流回路のシミュレーション結果
ダイオードは瞬間的にかなり大きな電力を消費している．

●ダイオード・ブリッジ整流回路の計算結果
　図6は，ログファイルに表示された，「.meas」コマンドによる電力の平均値の計算結果です．
　Prlが負荷抵抗の平均消費電力で約10.7Wです．Pdが4つのダイオードの平均消費電力の合計で，約3.4Wとなっています．これは負荷抵抗の消費電力の約32%で，ダイオードで消費される電力の比率がかなり高いことが分かります．

図6　ログファイルに表示された，「.meas」コマンドによる電力の平均値の計算結果
ダイオードの平均消費電力の合計は，負荷抵抗の消費電力の32%．

　図5のシミュレーション結果より，ダイオード・ブリッジを使用した整流回路では，電圧ドロップとダイオードで発生する，無駄な消費電力が大きいことが分かりました．

●電圧ドロップと消費電力を小さくできる整流回路
　電圧ドロップと無駄な消費電力を小さくするため，ダイオードの代わりにNchMOSトランジスタを使用する，理想ダイオード・ブリッジ・コントローラICを使用してみます．
　図7が，その理想ダイオード・ブリッジ・コントローラ(LT4320)を使用した整流回路をシミュレーションする回路です．

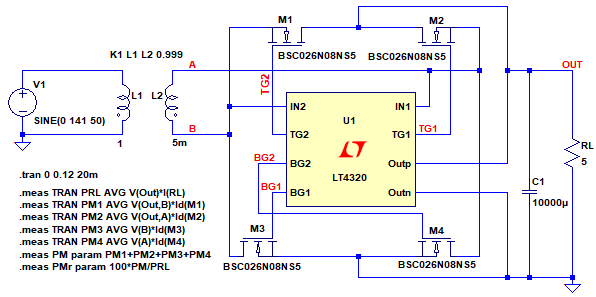
図7　理想ダイオード・ブリッジ・コントローラ(LT4320)を使用した整流回路
「.meas」コマンドで負荷抵抗とMOSトランジスタの消費電力の平均値を計算している．

　NchMOSトランジスタのM₁～M₄が，それぞれ図1のD₁～D₄と同様な働きをして，Out端子には両波整流出力が得られます．TG1～TG4が，MOSトランジスタのゲートをコントロールする端子です．LT4320はチャージ・ポンプによる昇圧回路を内蔵しており，入力電圧よりも高いゲート電圧を生成して，NchMOSトランジスタを駆動します．
　M₁～M₄のドレイン・ソース間に発生する電圧は，それぞれのMOSトランジスタのオン抵抗と流れる電流の積になります．図5で使用しているMOSトランジスタのオン抵抗は，3mΩ程度と非常に小さいため，電圧降下も非常に小さくなります．
　また，MOSトランジスタの消費電力は，ドレイン・ソース間電圧とドレイン電流の積になるため，MOSトランジスタの消費電力も非常に小さくなります．図4と同様に，「.meas」コマンドで負荷抵抗とMOSトランジスタの消費電力の平均値を計算しています．
　図8が図7のシミュレーション結果です．

図8　理想ダイオード・ブリッジ・コントローラ(LT4320)を使用した整流回路のシミュレーション結果
MOSトランジスタの消費電力は，かなり小さくなっていることが分かる．

　上段がA-B間の電圧とOut端子の電圧およびMOSトランジスタのゲート電圧です．Out端子のピーク電圧はA-B間のピーク電圧とほぼ同じ10Vとなっています．また，M₁のゲート電圧(V(TG1))は，A-B間のピーク電圧よりも8V高い18Vになっています．M₁のゲート・ソース電圧が8Vとなり，M₁のオン抵抗を十分小さくすることができています．
　下段が，負荷抵抗とMOSトランジスタの消費電力です．MOSトランジスタの消費電力は，図5のダイオードの消費電力に比べ，かなり小さくなっていることが分かります．

●電圧ドロップと消費電力を小さくできる整流回路の計算結果
　図9がログファイルに表示された，「.meas」コマンドによる電力の平均値の計算結果です．
　負荷抵抗の平均消費電力(Prl)は約18Wと，図5の結果よりも大きくなっていますが，4つのMOSトランジスタの平均消費電力の合計は，約0.2Wとかなり小さくなっています．これは負荷抵抗の消費電力の約1.2%で，無駄な電力消費がほとんどなくなっています．

図9　ログファイルに表示された，「.meas」コマンドによる電力の平均値の計算結果
MOSトランジスタの平均消費電力の合計は，負荷抵抗の消費電力の1.2%．

　以上，理想ダイオード・ブリッジ・コントローラによる全波整流回路について解説しました．最近では，スイッチング電源を使用した交流・直流変換回路が多くなっていますが，理想ダイオード・ブリッジ・コントローラを使用することで，スイッチング電源を使用せずに高効率電源を実現することができます．LT1430の詳しい使用方法はデータシートを参照してください．

◆参考・引用*文献
(1)アナログデバイセズ：LT1430データシート
(2)LTspice電源＆アナログ回路入門アーカイブ：家庭用電源から直流電源を作る整流回路

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice10_029.zip

●データ・ファイル内容
full_rect_D.asc：図4の回路
full_rect_D.plt：図5のグラフを描画するためのPlot settinngsファイル
LT4320.asc：図4の回路
LT4320.plt：図5のグラフを描画するためのPlot settinngsファイル