AC/DC変換のリプル率

■問題

【電源】

平賀　公久　Kimihisa Hiraga

　図1は，V1のAC(交流)をブリッジ回路により振幅が140V，周波数が50Hzへ全波整流し，抵抗(R₁)とコンデンサ(C₁)のリプル・フィルタでDC(直流)に変換するAC/DC変換回路です．
　図1のコンデンサ(C₁)を100μFで固定し，抵抗(R₁)を1.0kΩ，1.5kΩ，1.8kΩ，2.0kΩと変えた場合，outのリプル率が最も低くなるのは，(a)～(d)のどの抵抗値でしょうか．

図1　交流から直流を作るAC/DC変換回路
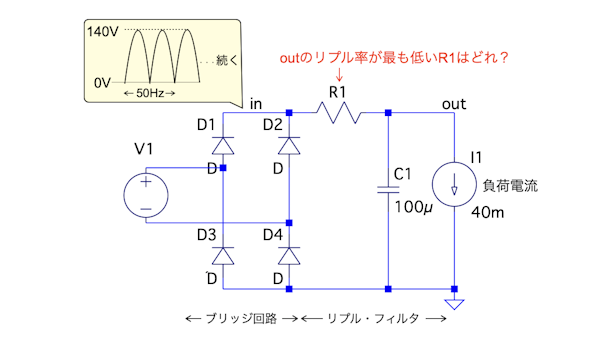
リプル率が最も低いR₁の抵抗はどれ？

(a) 1.0kΩ　(b) 1.5kΩ　(c) 1.8kΩ　(d) 2.0kΩ

■ヒント

　ACからDCへの変換の効率は，リプル率で表し，リプル率が低いほど，outの直流の電圧変動が小さくなり安定します．
　図1のリプル率は，「50Hzの第2次高調波成分÷全波整流の平均値」で計算します．第2次高調波成分は，抵抗(R₁)とコンデンサ(C₁)の時定数に関係します．

■解答

(d) 2.0kΩ

　図1のinに表した全波整流の平均値は，リプル・フィルタの抵抗(R₁)とコンデンサ(C₁)に関係なく同じ電圧になります．次にリプル・フィルタの時定数は，抵抗(R₁)とコンデンサ(C₁)の積であり，「R₁C₁」になります．リプル・フィルタは時定数が低いとoutの直流が時間と共にわずかかに変化して第2次高調波成分が生まれ，リプル率は高くなります．逆に時定数が高いと第2次高調波成分は低くなり，リプル率は低くなるのでoutの直流は安定します．
　この関係より，C₁が固定のときはR₁を高くするとリプル率は低くなるので，R₁が最も高い(d)の2kΩの場合，リプル率が最も低くなります．

■解説

●AC/DC変換の効率を表す指標としてリプル率を用いる
　オーディオ回路を安定に動作させるには，回路を動かす直流電圧が安定していることが求められます．直流電圧が安定すると，回路のバイアス電圧の変動が低くなります．直流電圧の変動は外来雑音のように見えることから，直流電圧が安定すると回路が安定することになります．AC/DC変換の回路例として，図1に示したブリッジ・ダイオードを使った全波整流回路とリプル・フィルタを組み合わせた回路がよく用いられます．このようなAC/DC変換回路の効率を表す指標としてリプル率が使われます．

●リプル率の定義
　リプル率は，ACからDCに変換したoutの波形の第2次高調波成分と，全波整流波形の平均値の比で表し，具体的には式1になります．　

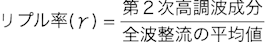・・・・・・・・・・・・・・・・・・・・・・・・(1)

　全波整流の平均値は，直流成分なので，直流成分に第2次高調波成分がどれくらいあるかを表しています．図1の例では，50HzのACを全波整流してDCに変換する回路なので，リプル率は50Hzの2倍の高調波になる100Hzの高調波成分と全波整流の平均値の比になります．

●回路定数から求めるリプル率の机上計算
　ここでは，図1の回路定数を使い，AC/DC変換のリプル率について机上計算します．図1において，outの電圧が時間と共にわずかに変動する波形のとき，outの波形のフーリエ級数は式2になります．

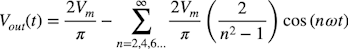・・・・・・・・・・・・・・・・・・・(2)

　式2中の右辺第一項「2Vm/π」は全波整流回路の平均値，右辺第二項は偶数次項（n=2次，4次，6次…）の高調波成分からなります．式2の右辺第一項である全波整流の平均値は，全波整流の振幅(Vm)から計算できます．図1の全波整流の振幅は「Vm=140V」なので式3になります．

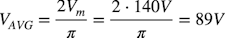・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　次に，式1のリプル率は50Hzの2倍の高調波（n=2）になる100Hzの高調波成分を使います．cos関数の最大値は1であることより，式2の右辺第二項の2次高調波成分は式4になります．

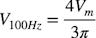・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4を実効値のRMSに変換すると式5になります．

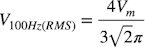・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5の電圧と抵抗（R₁）による電流は式6になり，コンデンサ（C₁）へ流れます．

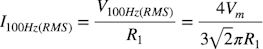・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式6の100Hzの電流は，コンデンサ（C₁）のリアクタンスにより，リプル電圧になり式7になります．

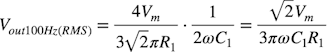・・・・・・・・・・・・・・・・・・・・(7)

　ここでのコンデンサ（C₁）のリアクタンスの周波数は100Hzなので，「1/2ωC₁」になります．
　式1へ式3の全波整流の平均値と，式7の第2次高調波成分を代入してリプル率を求めると式8になります．

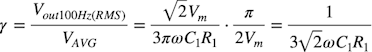・・・・・・・・・・・・・・・・・(8)

　式8を整理すると，リプル率は式9になります．このようにリプル率は50Hzの角周波数（ω）とコンデンサ（C₁）と抵抗（R₁）で求めることができます．

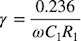・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

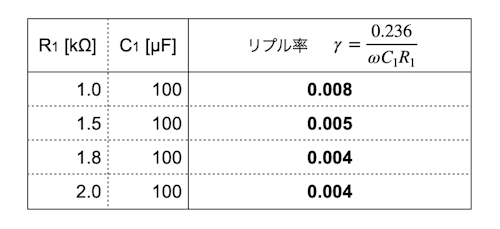
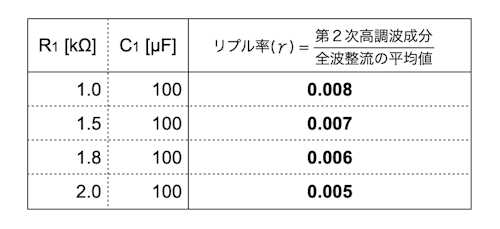
　表1は，式9を使いコンデンサ（C₁）を100μFで固定して，抵抗（R₁）を1.0kΩ，1.5kΩ，1.8kΩ，2.0kΩとしたときのリプル率になります．表1より抵抗（R₁）が高くなるとリプル率は低くなり，図1のoutの直流は安定します．

表1　R₁とC₁を使って計算したリプル率

●リプル率のシミュレーション
　図2は，図1の4つの抵抗のリプル率をシミュレーションで求める回路になります．図2ではドット・コマンド「.tran 0 10 0 100u」で，0秒から10秒までを100μsの間隔でtran解析し，outの波形を観測します．その後ドット・コマンド「.four 50Hz V(out)」でフーリエ変換して第2次高調波成分を求め，リプル率を求めます．「.options plotwinsize=0」は，シミュレーションのデータ圧縮をOFFにする指定で，フーリエ変換の精度が悪化しないようにしています．4つの抵抗は「.step param Res list 1k 1.5k 1.8k 2k」のステップ・コマンドにより抵抗値を変化させています．

図2　図1をシミュレーションする回路
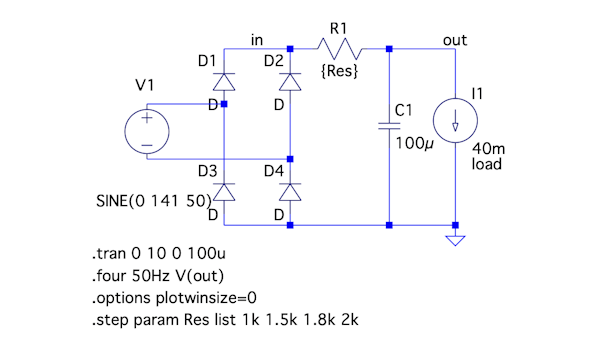
outの第2次高調波をフーリエ変換で調べ、リプル率を調べる．

　図3は，図2のシミュレーション結果で，全波整流の波形V(in)とoutの波形V(out)になります．抵抗(R₁)が高くなるほどoutの波形の振幅が低くなる様子が分かります．

図3　図2のシミュレーション結果
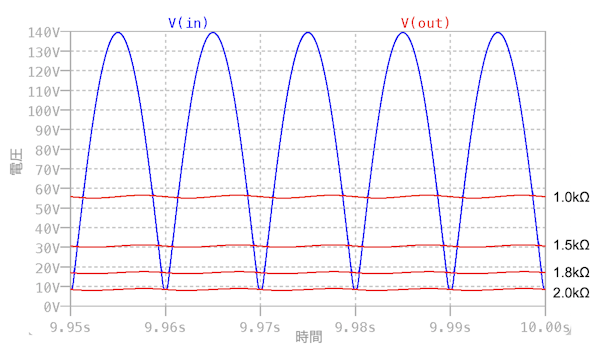
全波整流した波形をリプル・フィルタで平滑したプロット．

●第2次高調波成分からリプル率を求める
　次に，図3の4つの抵抗におけるV(out)についてフーリエ変換を実行後，第2次高調波成分を抜き出したものが以下の表2～表5になります．第2次高調波成分は「Harmonic Number」の「2」で示されており，具体的な第2次高調波成分は赤字で示しました．フーリエ変換の結果はログ・ファイル中にあり，回路図上で「Ctrl+L」（コントロール・キーとLを同時押し）で確認できます．

表2　R₁=1kΩ，C₁=100μFのoutのフーリエ変換結果