ギターの音がうねる「フェイザ」の試聴

■問題

【フィルタ回路】

小川　敦　Atsushi Ogawa

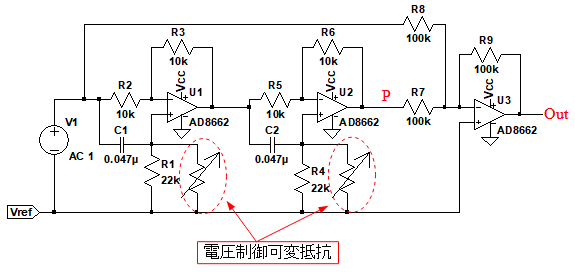
　図1は，エレキ・ギターに使われる，「フェイザ」と呼ばれるエフェクタの，回路の一部を簡略化したものです．回路図中にある，電圧制御可変抵抗の抵抗値を，低周波発振回路の出力で制御して，ギターの音色を変えます．
　図2は，電圧制御可変抵抗の抵抗値が無限大のときのOut端子とP点の周波数特性のグラフです．図1の周波数特性として正しいのは(a)～(d)のどれでしょうか．

図1　フェイザ・エフェクタの，回路の一部を簡略化したもの
電圧制御可変抵抗の抵抗値が無限大のときの周波数特性は？

図2　Out端子とP点の周波数特性のグラフ
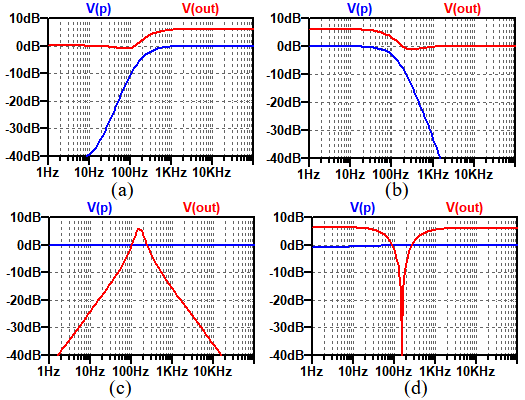
図1の周波数特性として正しいのはどれ？

(a)の周波数特性　(b)の周波数特性　(c)の周波数特性　(d)の周波数特性

■ヒント

　OPアンプ(U₃)は加算回路として動作します．そのため，In端子とP点の信号を加算したものが，Out端子に出力されます．OPアンプ(U₁，U₂)で構成されるフィルタが，どのような特性になるかということと合わせて考えれば，答えが分かります．

■解答

(d)の周波数特性

　OPアンプ(U₁，U₂)は，オールパス・フィルタを構成しています．オールパス・フィルタは，周波数を変えても振幅は変化せず，位相だけが変化するフィルタです．そのため，P点の振幅は周波数によらず，一定になります．
　オールパス・フィルタ出力と入力信号を加算すると，位相が同じときは振幅が2倍になります．そして，位相が180度ずれる周波数では，打ち消しあって振幅が小さくなります．つまり，Out端子はノッチ特性となります．このような周波数特性となっているのは(d)なので，正解は(d)の周波数特性ということになります．

■解説

●フェイザ・エフェクタの構成
　図3は，フェイザ・エフェクタ回路のブロック図です．フェイザは，可変位相シフト回路(オールパス・フィルタ＋電圧制御可変抵抗)と加算回路でノッチ・フィルタ(特定周波数の信号を除去する)を構成します．そしてそのノッチ・フィルタのノッチ周波数を，周期的に細かく変動させるエフェクタです．

図3　フェイザのブロック図
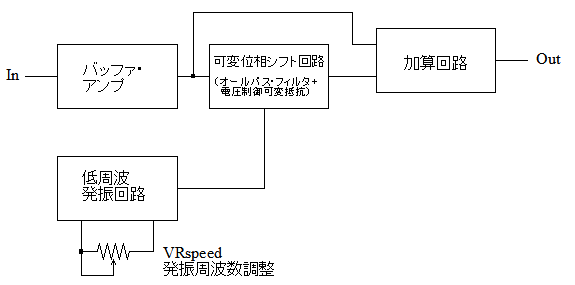
可変位相シフト回路と加算回路で構成したノッチ・フィルタを，低周波発振回路で制御

　低周波発振回路で発生させた数Hz～数十Hzの信号で，オールパス・フィルタのカットオフ周波数を変化させ，ノッチ周波数を変動させます．低周波発振回路の発振周波数は，可変抵抗器(VRspeed)で調整します．

●オールパス・フィルタの周波数特性
　図4は，OPアンプで構成した基本的なオールパス・フィルタです．

図4　OPアンプで構成した基本的なオールパス・フィルタ
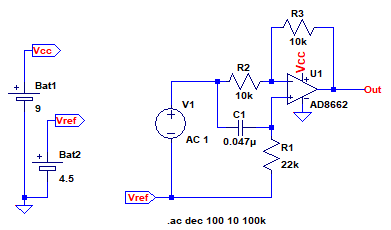
R₂=R₃とすると，ゲインは周波数に依存せず1となる．

　R₂=R₃とした場合，この回路の伝達関数は式1で表されます．

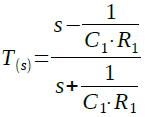・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　式1で「s=jω」と置き，絶対値を求めると，式2のように1にとなります．

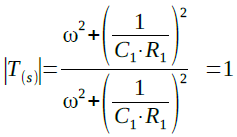・・・・・・・・・・・・・・・・・・・・・・・・(2)

　つまり，ゲインは周波数に依存しないことが分かります．この回路で位相が90度シフトする周波数は式3で計算することができます．

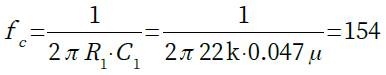・・・・・・・・・・・・・・・(3)

　図5は，図4のオールパス・フィルタのシミュレーション結果です．ゲインは周波数に依存せず，0dBとなっています．

図5　オールパス・フィルタのシミュレーション結果
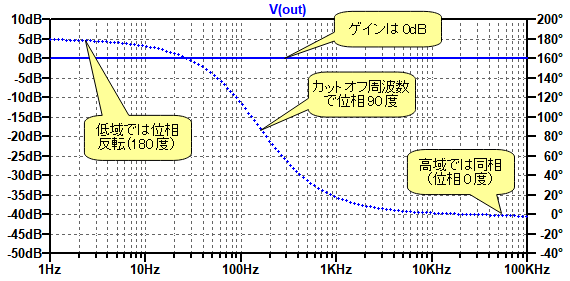
ゲインは周波数に依存せず，位相のみが変化している．

　また，低域では位相が反転していますが，周波数に応じて位相が変化し，高域では同相となっています．位相は180度から0度まで変化していることになります．
　なお，図4のC₁とR₁を入れ替えたものも，オールパス・フィルタとして動作します．その場合，Out端子の信号は，低域で同相となり，高域で位相反転となります．

●オールパス・フィルタ2段と加算回路の周波数特性
　図6は，オールパス・フィルタを2段従属接続し，その出力と入力信号を加算する加算回路を組み合わせた回路です．図1の回路をシュミレーションするための回路図になっています．

図6　オールパス・フィルタ2段と加算回路を組み合わせた回路
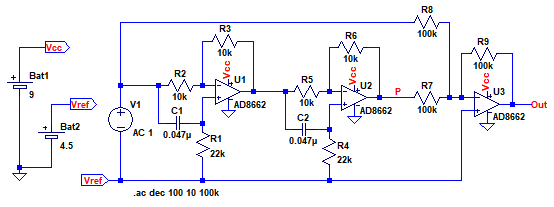
オールパス・フィルタ出力と入力信号を加算している．

　図7は図6のシミュレーション結果です．P点の振幅は周波数によらず一定になっています．また，P点の位相は0度から360度まで変化し，位相が180度回転した周波数で，Out端子の振幅が減少するノッチ特性となっています．

図7　オールパス・フィルタ2段と加算回路のシミュレーション結果
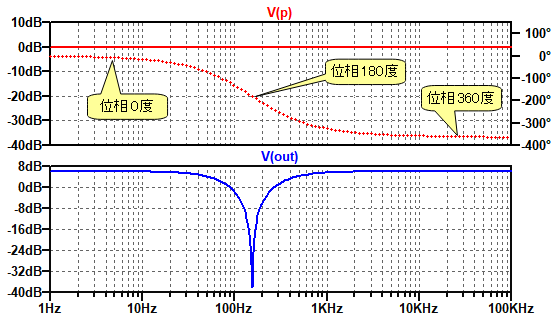
P点の位相が180度転した周波数で，Out端子の振幅が減少するノッチ特性となっている．

●JFETを電圧制御可変抵抗素子として使用する
　フェイザでは，位相シフト回路の位相特性をコントロールするために，電圧制御可変抵抗素子を使用します．フェイザの電圧制御可変抵抗素子としては，JFET(ジャンクションFET)がよく使用されています．JFETは，ゲート電圧を制御することで，ドレイン・ソース間の小信号抵抗(オン抵抗)を変化させることができます．
　図8は，JFETのゲート電圧とオン抵抗の関係を確認するための回路とそのシミュレーション結果です．ゲート電圧が-1.5V以上になると，急激にオン抵抗が小さくなっていることが分かります．

図8　JFETのゲート電圧とオン抵抗の関係を確認するための回路と結果
ゲート電圧が-1.5V以上になると，急激にオン抵抗が小さくなっている．

●JFETでオールパス・フィルタ4段の特性をコントロールする
　市販されているフェイザでは，オールパス・フィルタの段数を多くし，ノッチ特性となる周波数を増やしたものもあります．図9はオールパス・フィルタを4段に増やし，可変抵抗素子としてJFETを追加したものです．JFETのゲート・ソース間電圧(V_GS)を-1Vと-2Vに変化させ，周波数特性をシミュレーションします．

図9　オールパス・フィルタを4段に増やし，JFETを追加した回路
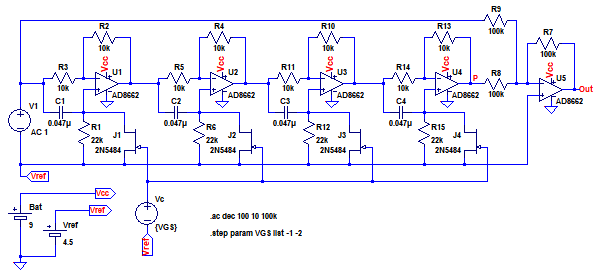
JFETのゲート・ソース間電圧を-1Vと-2Vに変化させ，周波数特性をシミュレーションする．

　図10が図9の回路のシミュレーション結果です．青線が「V_GS=-2V」のときの特性で，赤線が「V_GS=-1V」のときの特性です．V_GSの値により，オールパス・フィルタのカットオフ周波数がコントロールできていることが分かります．

図10　オールパス・フィルタ4段の場合のシミュレーション結果
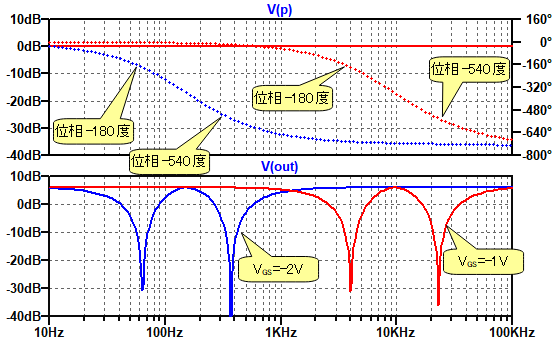
2つの周波数でノッチ特性となり，V_GSの値で特性が変化している．

　P点の位相は，それぞれ0度から-720度まで回転し，-180度のときと，-540度の2か所でOut端子の振幅が減少するノッチ特性となっています．

●可変位相回路と低周波発振回路の組み合わせ
　図11が，図9の可変位相回路と低周波発振回路を組み合わせた，フェイザをシミュレーションするための回路です．

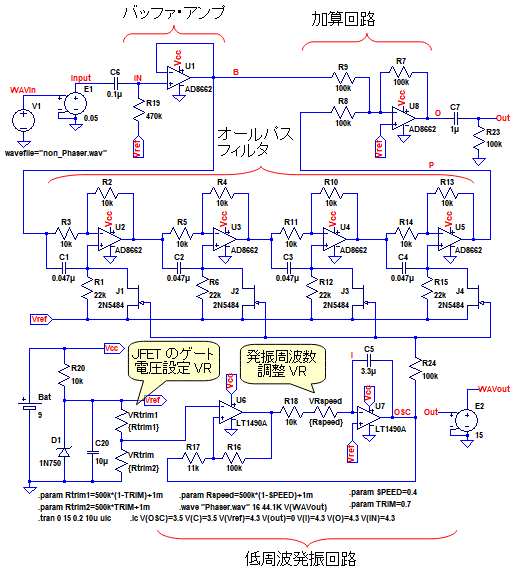
図11　可変位相回路と低周波発振回路を組み合わせた，フェイザのシミュレーション用回路
ギター音源を入力し，フェイザの効果を試聴する．

　低周波発振回路は，積分回路とヒステリシス・コンパレータを組み合わせたもので，三角波発振出力が得られます．発振周波数は可変抵抗器(VRspeed)で調整します．その摺動子の位置は，SPEEDという変数で設定します．
　低周波発振回路の出力はJFETのゲートに接続され，その直流電圧は，VRtrimという可変抵抗器で設定します．その摺動子の位置はTRIMという変数で設定します．この回路に，LTspiceのWAVファイルの入出力機能を利用して，ギター音源を入力し，フェイザの効果を試聴します．V₁の電圧を「wavefile="non_Phaser.wav"」とし，「.wave "phaser.wav" 16 44.1K V(WAVout)」というコマンドを追加します．

●フェイザの効果をシミュレーションして試聴する
　図11(Phaser_WAV.asc)のシミュレーションをスタートすると，図12のシミュレーション結果の表示が開始されます．出力電圧が安定するしてからWAVファイルに記録するために，シミュレーション開始0.2秒後から保存するよう「.tranコマンド」を設定しています．
　図12の上段がWAVファイルに記録されたギターの音源の波形で，下段がフェイザの出力波形です．シミュレーションが終了(約5分～10分)すると，回路図ファイルと同じフォルダに，「phaser.wav」というファイルが作られます．このファイルを再生することで，フェイザで加工された音を試聴することができます．加工前の「non_phaser.wav」と聞き比べてみてください．

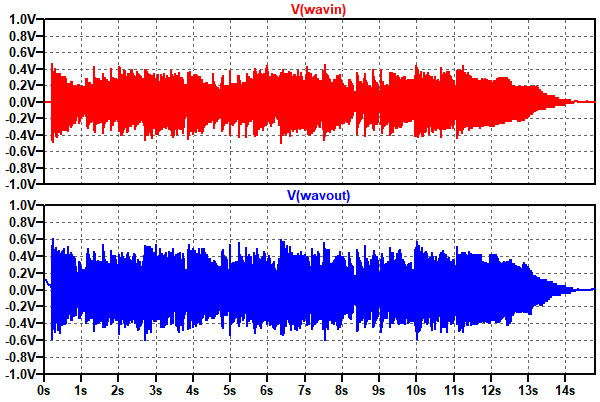
図12　ギター音源を入力したときのフェイザのシミュレーション結果
上段がギターの音源の波形で，下段がフェイザの出力波形．

　以上，フェイザ・エフェクタについて解説しました．回路図中の「SPEED」という変数を変えると，音色が変化します．また，図9のR₁₁の値を変えると，低周波発振回路の振幅が変化します．そして「TRIM」という変数で低周波発振回路の直流電圧が変化します．これらの値を変えることでJFETのコントロール特性を変えることができます．「SPEED」変数の変更と合わせて，いろいろシミュレーションしてみてください．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice9_031.zip

●データ・ファイル内容
All_Pass_AC.asc：図4の回路
phaser2_AC.asc：図6の回路
phaser2_AC.plt：図7のグラフを描画するためのPlot settinngsファイル
phaser4_JFET_AC.asc：図9の回路
phaser4_JFET_AC.plt：図10のグラフを描画するためのPlot settinngsファイル
Phaser_WAV.asc：図11の回路
Phaser_WAV.plt：図12のグラフを描画するためのPlot settinngsファイル
non_Phaser.wav:入力音源ファイル