抵抗の値が大きくなれば雑音はどうなる？

■問題

【ノイズ】

平賀　公久　Kimihisa Hiraga

　図1は，R₁の抵抗に並列容量(C_p)があるときのoutの雑音電圧を調べる回路です．周波数が0Hzから無限大周波数までの全周波数帯域内におけるoutの雑音電圧として，正しい関係は(a)～(d)のどれでしょうか．ただし雑音を測定する温度は27℃とします．

図1　抵抗に並列容量がある回路
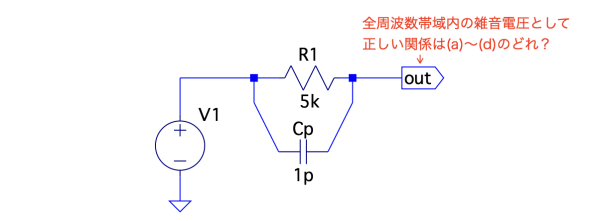
全周波数帯域内のoutの雑音電圧として正しい関係はどれ？

(a) 無限大周波数までなので，outの雑音電圧は無限大になる
(b) 全周波数帯域内のoutの雑音電圧はR₁で決まる
(c) 全周波数帯域内のoutの雑音電圧はC_pで決まる
(d) 全周波数帯域内のoutの雑音電圧はR₁とC_pで決まる

■ヒント

　全周波数帯域内の雑音は雑音帯域幅に関係します．雑音の発生源と雑音帯域幅を使って検討すると分かります．

■解答

(c) 全周波数帯域内のoutの雑音電圧はC_pで決まる

　図1のoutの雑音電圧は，R₁の抵抗で発生する熱雑音電圧が発生源です．outの雑音電圧をV_onoiseとすると，V_onoise²は「V_onoise²=4kTR₁f_BW」になります．ここでkはボルツマン定数，Tは絶対温度で27℃のとき300Kです．そして，f_BWは雑音帯域幅で「f_BW=1/4C_pR₁」になります．f_BWを先程のV_onoise²の式に入れて整理すると「V_onoise= (kT/C_p)^1/2」になります．kは定数，Tは一定なので，全周波数帯域内のoutの雑音電圧は並列容量のC_pで決まり，正解は(c)になります．

■解説

●抵抗の熱雑音
　図1の雑音の発生源は，抵抗の熱雑音になります．熱雑音は導体中の電荷キャリアが熱で励起され，不規則に動く熱擾乱から発生する雑音です．図1ではこの熱雑音がoutに現れます．outの雑音電圧をV_onoiseとすると，V_onoise²は式1になります．ここで式1右辺のkはボルツマン定数で「k=1.38×10^-23J/K」，Tは絶対温度で27℃のとき「T=300K」，R₁は抵抗値で「R₁=5kΩ」です．f_BWは雑音帯域幅で並列容量(C_p)により変わります．0Hz～無限大周波数までの全周波数帯域内の雑音は,雑音帯域幅(f_BW)に関係します．f_BWが高いと全周波数帯域内の雑音も高くなります．
　式1は,「抵抗の雑音を測ると，並列容量は無いのでf_BWは無限大になり，全周波数帯域内の雑音は無限大になる？」と疑問に思うことがあります．

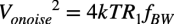・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　これは理想抵抗の計算はそうなりますが，2つの端子が電極になり，空気などを介して何らかの並列容量があるため，全周波数帯域内の雑音は無限大になりません．

●雑音帯域幅を検討する回路
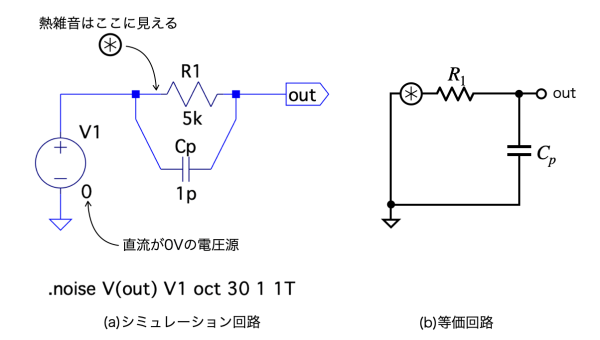
　次に図2(a)を用いて図1の雑音帯域幅(f_BW)について検討します．図2(a)は，図1と同じ回路ですが，雑音の周波数特性を調べるため「.noiseコマンド」を加えた回路になります．具体的には「.noise V(out) V1 oct 30 1 1T」の指定で，V1からoutまでの雑音を，1Hzから1THzまで周波数が2倍あたり30ポイントで，雑音の周波数特性を調べます．
　図2(b)は，図2(a)の等価回路になります．R₁の左にある抵抗の熱雑音は，R₁とC_pの1次ロー・パス・フィルタを通過してoutに現れます．図2(b)の等価回路より，outの雑音電圧の周波数特性は，1次ロー・パス・フィルタの周波数特性になります．以降では，図2(a)のシミュレーション結果を元に，1次ロー・パス・フィルタの雑音帯域幅(f_BW)を検討します．

図2　図1の雑音帯域幅について検討する回路

●1次ロー・パス・フィルタの雑音帯域幅
　図3は，図2(a)のシミュレーション結果です．Y軸がV_onoise²，X軸が周波数になります．X軸は周波数の変化で雑音の変化が分かりやすいように，対数の軸から線形の軸に変えて，1Hz～400MHzをプロットしています．赤のプロットは1次ロー・パス・フィルタの周波数特性になります．周波数が0Hzから無限大周波数までの全周波数帯域内の雑音は，赤のプロットの内側の面積になります．
　1次ロー・パス・フィルタの雑音帯域幅(f_BW)は，赤のプロットを0Hz～無限大周波数で積分した面積と「|T₀|²×f_BW」の四角形の面積を等しくするf_BWになります．ここで「|T₀|²」は低周波における雑音になります．このような四角形にすると，低周波の雑音と雑音帯域幅から全周波数帯域の雑音を簡単に求めることができます．

図3　図2(a)のシミュレーション結果
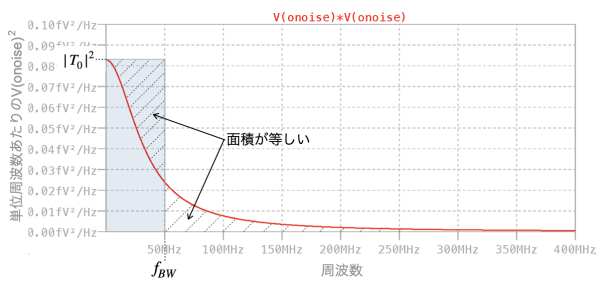
雑音帯域幅(f_BW)は，赤のプロットを0Hz～無限大で積分した面積と「|T₀|²×f_BW」の面積を等しくするf_BWになる．

●雑音帯域幅の机上計算
　ここでは，1次ロー・パス・フィルタを通過した後の雑音帯域幅(f_BW)を机上計算で求めます．1次ロー・パス・フィルタの伝達関数は式2になります．

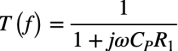・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　図3に示した雑音帯域幅の定義より，式2を0Hz～無限大周波数で積分し，|T₀|²で除算した値が雑音帯域幅(f_BW)なので，式3になります．

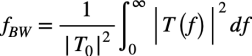・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3へ式2を代入して整理すると，雑音帯域幅(f_BW)は式4になります．式4より，1次ロー・パス・フィルタを通過した後の雑音帯域幅(f_BW)は,抵抗(R₁)と並列容量(C_p)で決まります．

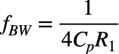・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

●抵抗に並列容量があるときの全周波数範囲内の雑音
　式1の抵抗の熱雑音と式4の雑音帯域幅を使って，図1の抵抗に並列容量があるときの全周波数範囲の雑音を計算して答え合わせをします．式1へ式4を代入してV_onoiseを求めると式5になります．

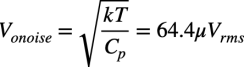・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5より全周波数範囲内の雑音は，ボルツマン定数(k)と絶対温度(T)と並列容量(C_p)で計算できます．ボルツマン定数は一定，絶対温度は図1の温度が27℃固定のとき一定になります．これよりoutの全周波数帯域内の雑音は並列容量のC_pで決まり，正解は(c)になります．具体的な雑音の値は，ボルツマン定数「k=1.38×10^-23J/K」，絶対温度は27℃のとき「T=300K」，C_pは「C_p =1pF」を入れると64.4μV_rmsになります．

●1Hz～1THzの雑音をシミュレーション
　シミュレーションは，0Hzと無限大周波数の指定ができません．代わりに低い周波数は1Hz，高い周波数は，雑音帯域幅より十分高い周波数にします．具体的には，雑音帯域幅を式4で計算すると「f_BW=50MHz」なので，雑音帯域幅より十分高い1THzまでのシミュレーションとします．
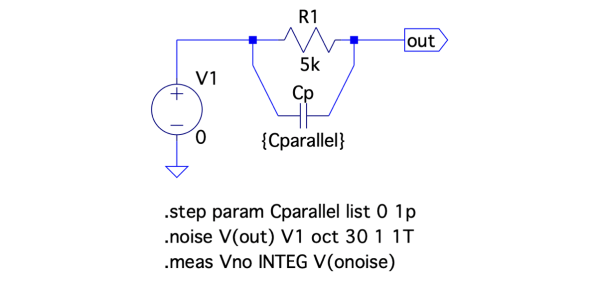
　図4は，図1と同じ回路ですが，並列容量が無いとき「C_p=0F」と，有るとき「C_p=1pF」を「.stepコマンド」を使って「.step param Cparallel list 0 1p」で変えています．そして「.noise V(out) V1 oct 30 1 1T」のコマンドで，1Hz～1THz間の雑音の周波数特性を調べます．調べた雑音の周波数特性より「.meas Vno INTEG V(onoise)」のコマンドで積分し，1Hz～1THz間の雑音を測定します．測定結果は変数Vnoに入り，シミュレーション後のログ・ファイル中に記録されます．

図4　並列容量が無しの場合と1pFの場合の雑音を調べる回路

●1Hz～1THzの雑音のシミュレーション結果
　図5は，図4の雑音の周波数特性になります．青のプロットは並列容量が無い理想の状態で，周波数が高くなり，無限大周波数になっても同じ値になります．一方，赤のプロットは並列容量が1pFの状態で，1次ロー・パス・フィルタを通過した周波数特性になります．

図5　図4のシミュレーション結果

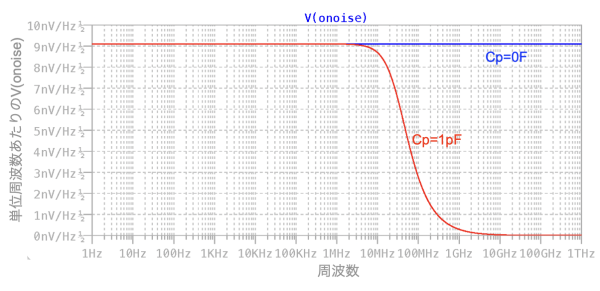
　図6は，図4のシミュレーション後のログ・ファイルのスクリーン・ショットになります．「.measコマンド」の測定結果はここで確認できます．図6のstep1は「C_p=0F」の並列容量が無い理想の状態で，1Hz～1THz間の雑音は9.1mV_rmsになります．周波数が無限大になると1THz以上の雑音も加わるので，全周波数帯域内の雑音は無限大になります．しかし，実際の抵抗は，何らかの並列容量が有るので，この状態にはなりません．
　step2は「C_p=1pF」の並列容量が有る状態で，積分した雑音は64.4μV_rmsになります．「C_p=1pF」の雑音は，先程の式5で机上計算した全周波数範囲内の雑音と同じになります．この結果からも，式5で0Hz～無限大周波数までの全周波数帯域内の雑音が机上計算できることが分かります．

図6　図4の1Hz～1THz間の雑音を.measコマンドで測定した結果
並列容量が1pFのとき，64.4μV_rmsになり，机上計算と一致する．

●抵抗を変えたときのシミュレーション
　最後に，抵抗が変化しても式5で決まる雑音になるのかを調べます．図7は，並列容量を「C_p=1pF」で固定し，R₁の抵抗を「.step param Res list 1k 2k 5k 10k」を用いて1kΩ，2kΩ，5kΩ，10kΩの4種類に変えたときの雑音を調べる回路になります．シミュレーションは図4と同じやり方になります．

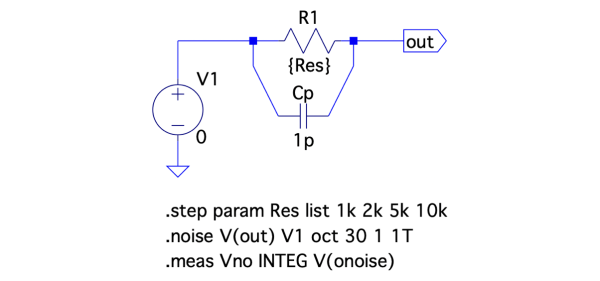
図7　並列容量を1pFで固定し，R₁の抵抗を変えたときのシミュレーション回路
R₁は1kΩ，2kΩ，5kΩ，10kΩの4種類．

　図8は，図7のV_onoiseの周波数特性をプロットしました．4種類の抵抗は異なるので，低周波の雑音は異なります．しかし，抵抗が変わると周波数特性が変ります．このとき，式4の雑音帯域幅も変わります．

図8　V_onoiseの周波数特性をプロット

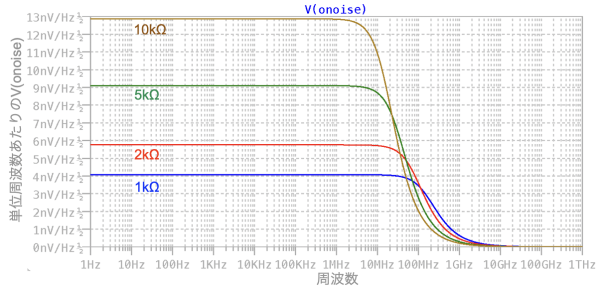
　図9は，図7の「.measコマンド」で調べた1Hz～1THz間の雑音の測定結果になります．step1が「R₁=1kΩ」，step2が「R₁=2kΩ」，step3が「R₁=5kΩ」，step4が「R₁=10kΩ」です．図9からも分かるように1Hz～1THz間の雑音は64.4μV_rmsになり，outの雑音は式5で決まるのが分かります．

図9　図7の1Hz～1THz間の雑音を.measコマンドで測定した結果
抵抗を変えても1Hz～1THz間の雑音は64.4μV_rmsになる．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice9_030.zip

●データ・ファイル内容
noise1.asc：図2(a)の回路
noise1.plt：図2(a)のプロットを指定するファイル
noise2.asc：図4の回路
noise2.plt：図4のプロットを指定するファイル
noise3.asc：図7の回路
noise3.plt：図7のプロットを指定するファイル