周波数応答と時間応答の関係

■問題

【増幅回路】

平賀　公久　Kimihisa Hiraga

　図1は，周波数応答のコーナ周波数(f_C)が68kHzのオーディオ・アンプです．このアンプの入力にはV1の矩形波を加えています．このときoutの波形は矩形波に近くなりますが，立ち上がり時間が発生します．この立ち上がり時間として正しいのは(a)～(d)のどれでしょうか．
　ただし，コーナ周波数は，低周波の一定のゲインから-3dB減衰する周波数です．そして，コーナ周波数より高い周波数では-6dB/octで減衰します.

図1　コーナ周波数が68kHzのオーディオ・アンプ
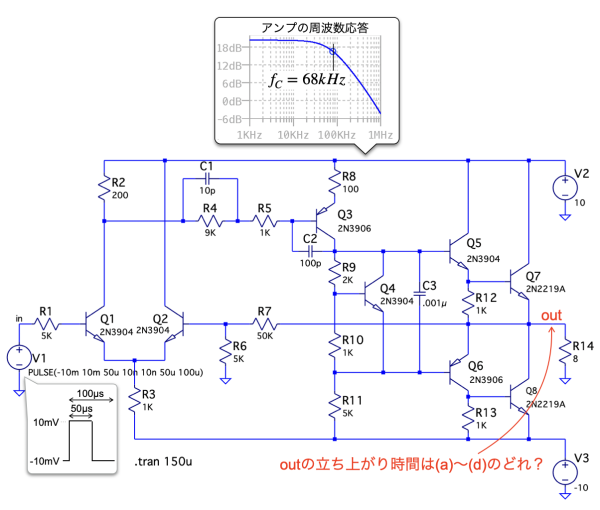
この回路は，LTspiceのEducationalフォルダ(\LTspiceXVII\examples\Educational)のaudioamp.ascです．
振幅が±10mVの矩形波を入力したとき，outの立ち上がり時間はいくつ？

(a) 0.9μs，(b) 2.3μs，(c) 5.1μs，(d) 14.7μs

■ヒント

　立ち上がり時間は，outの波形が10%から90%へ推移する時間です．この立ち上がり時間は，コーナ周波数に関係する時定数で決まります.

■解答

(c) 5.1μs

　図1のアンプの入力に，立ち上がり速度が極めて速い矩形波を入力したときを考えます．アンプは低周波では一定のゲインですが，コーナ周波数より高周波側では-6dB/oct(周波数が2倍になると-6dB減衰する)の周波数応答になります．低周波の一定のゲインから-3dB減衰するコーナ周波数をf_Cとすると，立ち上がり時間は「t_r=0.35/f_C」で求まります．f_Cは68kHzなので，立ち上がり時間は(c) 5.1μsになります．

■解説

●周波数応答により出力の時間応答が発生する
　アンプの入力信号は正弦波だけでなく，振幅が急激に変化する矩形波のような信号もあります．今回は図1のアンプの周波数応答と時間応答の関係について調べます.
　図2は，三角形のアンプ記号で表したアンプの入力に，矩形波の下限の振幅から上限の振幅に推移する信号を加えたときの波形を図示しました．このような階段状に急激に変化する入力信号はステップ入力といいます．
　図2のアンプは，低周波のゲインは一定で，そのゲインから-3dBになるコーナ周波数を通り，-6dB/octの傾きで減衰する周波数応答です．この周波数応答のアンプへステップ入力を加えると，出力波形が滑らかになり，立ち上がり時間が発生します．立ち上がり時間は，出力の波形が10%から90%へ推移する時間になります．この立ち上がり時間以上の速さで推移する入力信号を加えても出力は追随できません．同じことが矩形波の上限の振幅から下限の振幅に推移するステップ入力のとき，立ち下がり時間が発生します．立ち上がり時間と立ち下がり時間は，アンプのコーナ周波数に関係しています.

図2　アンプの周波数応答と時間応答の波形
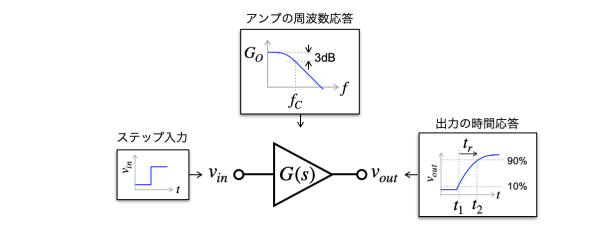
出力の立ち上がり時間(t_r)はコーナ周波数(f_C)に関係している.

●アンプの周波数応答と時間応答の関係を机上計算
　ここでは，アンプのコーナ周波数(f_C)と立ち上がり時間(t_r)の関係を机上計算します．図2のアンプの周波数応答は，低周波のゲインをG_Oとすると式1になります．

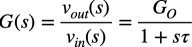・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

ここでsはラプラス演算子で「s=jω」です.

　式1中のτは時定数でコーナ周波数を使って表すと式2になります.

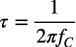・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　計算式が複雑になるので，式2の2πf_Cの項を式3で表します.

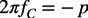・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式1へステップ入力したときのoutの時間応答は式4になります.

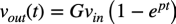・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4を使ってoutの振幅が10%になるときは式5になります.

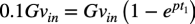・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5からoutの振幅が10%になるときの時間t1は式6になります.

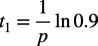・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　同じように，式4を使ってoutの振幅が90%になるときは式7になります.

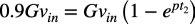・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式7からoutの振幅が90%になるときの時間t₂は式8になります.

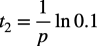・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　立ち上がり時間(t_r)は，t₂からt1を減じた時間なので式9になります.

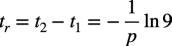・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　式9へ式3を入れて整理すると，コーナ周波数と立ち上がり時間の関係は式10になります.

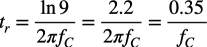・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　式10へ図1のコーナ周波数である68kHzを入れると，立ち上がり時間は式11の5.1μsになります.

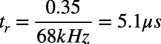・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　式10に示したアンプの周波数応答と時間応答の関係は，入力に小信号の矩形波が加わったときのoutの時間応答を求めるときによく使います．また他のアンプ回路でもこの関係が使えるので覚えておくと便利です.
　コーナ周波数(f_C)と立ち下がり時間(t_f)の関係は，矩形波の上限の振幅から下限の振幅に推移するステップ信号を加え，式1～式10と同じ検討をすると「t_r=t_f」になります．

●アンプの周波数応答をシミュレーションで調べる
　図3は，図1のアンプのゲイン周波数特性を調べる回路になります．シミュレーションは「.ac oct 10 1 1Meg」のコマンドで1Hz～1MHz間を周波数が2倍あたり10ポイントでスイープしてoutまでのゲインを調べます．また低周波の最大ゲインから-3dBになるコーナ周波数を「.meas」コマンドで調べます.

図3　図1の周波数応答をシミュレーションする回路
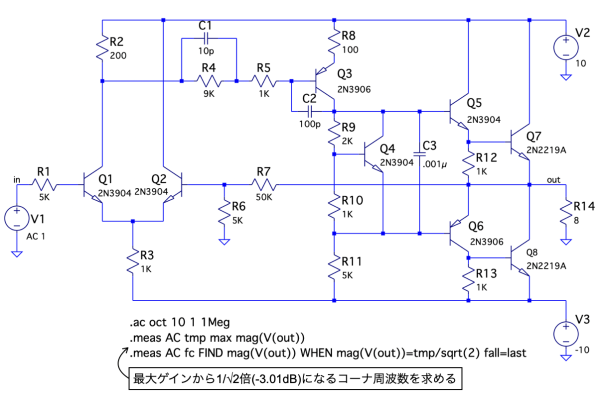
低周波のゲインから-3dBになるコーナ周波数を「.meas」で調べる.

　図4は，図3のシミュレーション結果でゲイン周波数特性をプロットしました．低周波の最大ゲインは20.3dBで，コーナ周波数より高周波側では-6dB/octで減衰します.

図4　図3のシミュレーション結果

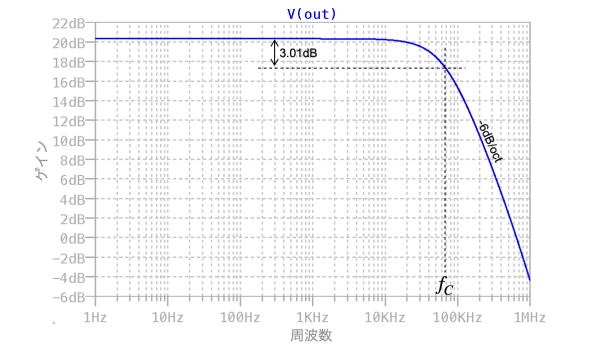
　図5は，コーナ周波数について「.meas」コマンドで調べた結果です．「.meas」コマンドの結果はログ・ファイル中にあるので，「Ctrl+L」(コントロールキーとLキーを同時押し)で表示できます．図5より低周波の最大ゲインから-3dBになるコーナ周波数は，冒頭の問題文で示した68kHzであることが分かります.

図5　図3のコーナ周波数を調べた結果
コーナ周波数は68kHzになる.

●アンプの時間応答をシミュレーションで調べる
　ここからは，図6の回路を使い，アンプの立ち上がり時間と立ち下がり時間をシミュレーションで調べて答え合わせをします．図6は，図1と同じ回路ですが，立ち上がり時間(t_r)と立ち下がり時間(t_f)を「.meas」コマンドで調べるため追加したものになります．シミュレーションは「.tran 150μ」のコマンドで，0s～150μs間をtran解析し，outの時間応答を調べます.

図6　図1のoutの時間応答をシミュレーションする回路.
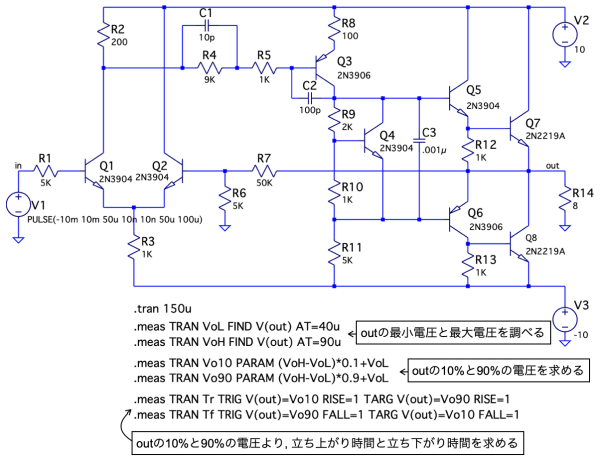
outの立ち上がり時間(t_r)と立ち下がり時間(t_f)を「.meas」で調べる.

　図7は，図6のシミュレーション結果でoutの波形とinの波形をプロットしました.　入力となるinの波形は振幅が±10mVの矩形波で，アンプで増幅後のoutの波形は立ち上がり時間(t_r)と立ち下がり時間(t_f)が発生しています.

図7　図6のシミュレーション結果.

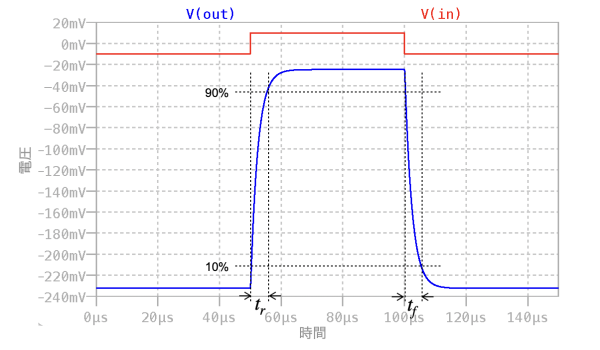
　図8は，立ち上がり時間(t_r)と立ち下がり時間(t_f)について「.meas」コマンドで調べた結果をスクリーン・ショットしました．図8より立ち下がり時間(t_f)は式11で机上計算した5.1μsと同じになるのが分かります．また立ち下がり時間(t_f)も同じになります.

図8　図6の立ち上がり時間(t_r)と立ち下がり時間(t_f)を調べた結果
立ち上がり時間と立ち下がり時間は5.1μsになる．

　以上，オーディオ・アンプの周波数応答と時間応答の関係について解説しました．実際のアンプは，無限周波数まで増幅する理想アンプでなく，高い周波数ではゲインが減衰する特性になるので，立ち上がり時間と立ち下がり時間が発生します．そこで，式10からコーナ周波数と立ち上がり時間，または，立ち下がり時間の関係を示しました．
　ここでの解説は，アンプの「コーナ周波数より立ち上がり時間が分かる」という解説ですが，「増幅後に欲しい立ち上がり時間から必要なコーナ周波数を設定する」という逆算した設計にも使えると思います．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice9_022.zip

●データ・ファイル内容
audioamp_closeloop.asc：図3の回路
audioamp_closeloop.plt：図3のプロットを指定するファイル
audioamp_tran.asc：図6の回路
audioamp_tran.plt：図6のプロットを指定するファイル