オーディオ・アンプのラウドネス・コントロール回路とは?

■問題

【フィルタ回路】

小川　敦　Atsushi Ogawa

　図1は，オーディオ・アンプに搭載された，ラウドネス・コントロール回路です．VR₁は，センター・タップ付きの4端子50kΩの可変抵抗器(ボリューム)です．センター・タップにはC₁とC₂が接続され，VR₁の摺動子の位置を変えることで，音量を変えることができます．VR₁の摺動子の位置がセンターのとき，Out端子(パワー・アンプの入力)の周波数特性として正しいのは，図2の(a)～(d)のどれでしょうか．

図1　オーディオ・アンプに搭載された，ラウドネス・コントロール回路
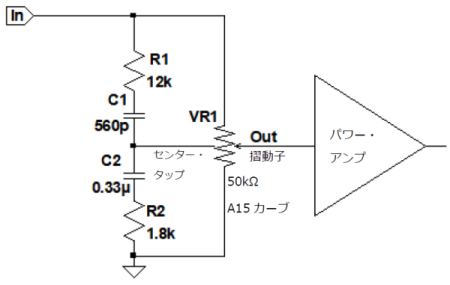
センター・タップ付きの4端子50kΩの可変抵抗器(ボリューム)を使用している．

図2　ラウドネス・コントロール回路の周波数特性
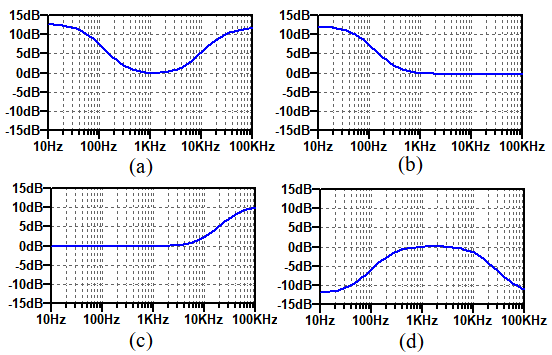
図2のグラフは，1kHが0dBになるように，それぞれ補正している．

(a)の周波数特性　(b)の周波数特性　(c)の周波数特性　(d)の周波数特性

■ヒント

　どのような周波数特性になるかを考えるとき，周波数の高域と低域それぞれの近似回路を作ると，直感的に考えやすくなります．なお，可変抵抗器の特性に関しては「LTspiceで学ぶオーディオ回路入門 017：ボリューム・コントロールに使用される可変抵抗器の特性」を参照してください．

■解答

(a)の周波数特性

　低域周波数領域では，C₁をオープンとみなした等価回路で特性を考えます．その等価回路では，VR₁の摺動子(センター)よりも上の抵抗とC₂により，「カットオフ周波数の低いロー・パス・フィルター」が構成されます．そのため，中域周波数を基準に考えると低域が増強された特性になります．
　高域周波数領域では，C₂をショートとみなした等価回路で特性を考えます．その等価回路では，高域でC₁のインピーダンスが小さくなることで，高域の減衰量が少なくなり，中域周波数を基準に考えると高域が増強された特性になります．
　つまり，中域周波数を基準に考えた場合，低域，高域ともに増強されたような特性になります．このような周波数特性になっているのは(a)なので，正解は(a)の周波数特性ということになります．

■解説

●ラウドネス・コントロール回路とは
　図3は，人間が同じ大きさの音と感じる音圧レベルを，音圧を変えて周波数ごとにプロットしたものです．この曲線は，等ラウドネス・レベル曲線⁽¹⁾と呼ばれています．なお，この特性は1950年代にISO226という国際規格になっています．その後，日本の研究成果により，2003年に，図3の赤線のように規格が改定されています．
　図3を見ると，音圧が小さくなると，低音と高音が聞こえづらくなっていることが分かります．そのため，オーディオ・アンプのボリューム・コントロール回路で，ボリュームを絞ったときに，自動的に低音と高音を増強するような回路が考案されました．このような，ボリューム位置により，低音と高音を増強する機能を持った回路を，ラウドネス・コントロール回路と呼んでいます．

図3　等ラウドネス・レベル曲線⁽¹⁾
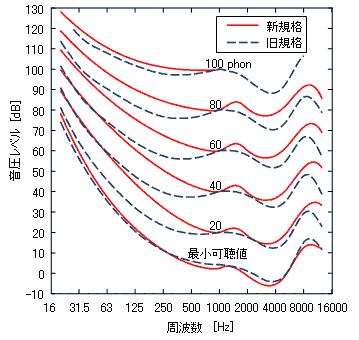
人間が同じ大きさの音と感じる音圧レベルを，周波数ごとにプロットした図．

●ラウドネス・コントロール回路の解析
　図4は，図1の回路の可変抵抗器を固定抵抗で書き換えたものです．A15カーブの可変抵抗器は，摺動子がセンターの位置にあるとき，摺動子とGND間の抵抗(R_B)は全体の抵抗の15%になります．
　全体の抵抗が50kΩなので，R_Bは7.5kΩでR_Aは42.5kΩになります．この回路の周波数特性を正確に解析するのは煩雑なので，低域周波数領域と高域周波数領域に分けて，低域と高域それぞれの近似回路を考えます．

図4　固定抵抗に置き換えたラウドネス・コントロール回路
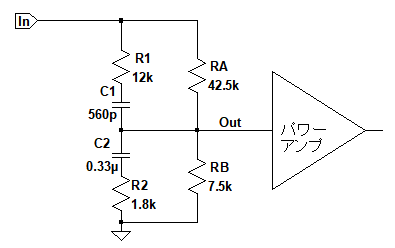
可変抵抗器をR_AとR_Bの2つの抵抗に置き換えている．

●ラウドネス・コントロール回路の低域周波数領域の解析
　図5は，ラウドネス・コントロール回路の低域周波数領域の特性を考えるための近似回路です．図3のC₁は低域周波数領域ではインピーダンスが高いため，無視できるものとして，C₁，R₁を外してあります．

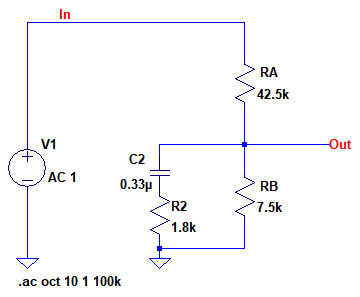
図5　ラウドネス・コントロール回路の低域周波数領域の特性を考えるための近似回路
図4のC₁は低域周波数領域ではインピーダンスが高いため，無視している．

　図4の回路の伝達関数は式1で表されます．

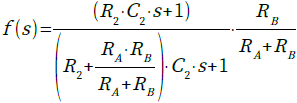・・・・・・・・・・・・・・・・・・・・・(1)

　直流領域では，入力信号はR_AとR_Bで分圧されるため，ゲイン(G_DC)は式2で表されます．

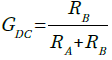・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式1の分母の時定数(抵抗とコンデンサの積)で決まるカットオフ周波数(f₁)以上で，ゲインが減衰を始めます．f₁は式3で求められます．

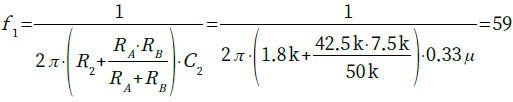・・・・・・・(3)

　もう少し周波数が高くなると，分子の時定数(抵抗とコンデンサの積)で決まる周波数(f₂)で減衰が停止し，フラットな周波数特性になります．f₂は式4で求められます．

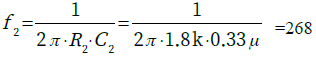・・・・・・・・・・・・・・・・・・・・(4)

　フラットな周波特性になったときのゲイン(G_Mid1)は，式5で表されます．

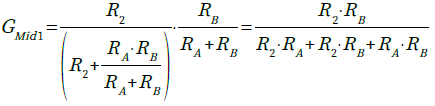・・・・・・・・・・・・(5)

　図6は，図5のシミュレーション結果です.

図6　図5のシミュレーション結果
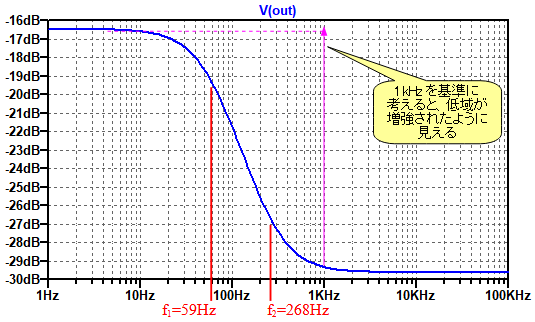
ロー・パス特性となっているが，1kHzを基準に考えると，低域のゲインが大きくなったように見える．

　図6は，高域が減衰するロー・パス特性となっていますが，1kHzを基準に考えると，低域のゲインが大きくなったように見えます．見かけ上の低域のゲイン増大量(G_LB)は式6で計算できます．

・・・・・(6)

●ラウドネス・コントロール回路の高域周波数領域の解析
　図7は，ラウドネス・コントロール回路の高域周波数領域の特性を考えるための近似回路です．図3のC₂は高域周波数領域ではインピーダンスが低いため，ショートしています．

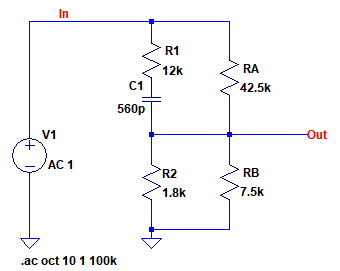
図7　ラウドネス・コントロール回路の高域周波数領域の特性を考えるための近似回路
図3のC₂は高域周波数領域ではインピーダンスが低いため，ショートしている．

　R₂とR_Bの並列抵抗値をR_B2とすると，R_B2は式7で表されます．

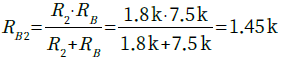・・・・・・・・・・・・・・・・・・・・・・(7)

　R_B2を使用すると，図6の回路の伝達関数は式8で表されます．

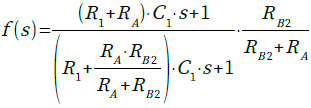・・・・・・・・・・・・・・・・・・・・(8)

　C₁が無視できる中音域のゲイン(G_Mid2)は式9で表されます．

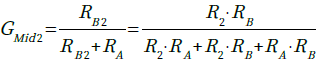・・・・・・・・・・・・・・・・・・・(9)

　G_Mid2は式5のGMid1と同じ式になります．そして式8の分子の時定数(抵抗とコンデンサの積)で決まる周波数(f₃)でゲインが上昇を始めます．f₃は式10で求められます．

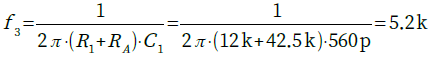・・・・・・・・・・・・(10)

　式8の分母の時定数(抵抗とコンデンサの積)で決まる周波数(f₄)で上昇が停止し，フラットな周波数特性に戻ります．f₄は式11で求められます．

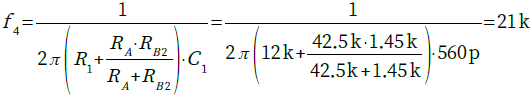・・・・・(11)

　図8が図7のシミュレーション結果です．

図8　図7のシミュレーション結果
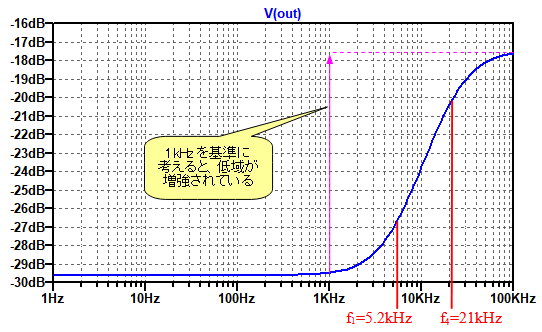
ハイ・パス特性となっており，1kHzを基準に考えると，高域のゲインが大きくなっている．

　図8は，ハイ・パス特性となっており，1kHzを基準に考えると，高域のゲインが大きくなっています．高域のゲイン増大量(G_HB)は式12で計算できます．

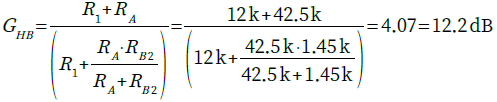・・・・・・・・(12)

●ラウドネス・コントロール回路の特性をシミュレーションする
　図9は，ラウドネス・コントロール回路の特性をシミュレーションするための回路です．通常の可変抵抗器は2本の抵抗で表現できますが，センター・タップ付きの可変抵抗器を表現するため，R_A～R_Dの4つの抵抗を使用しています．

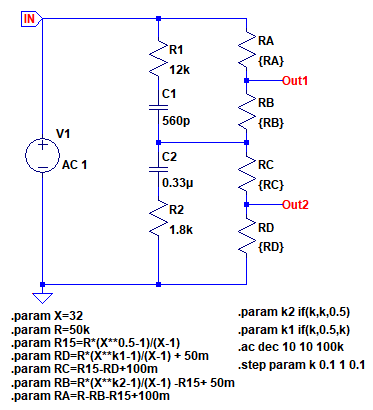
図9　ラウドネス・コントロール回路の特性をシミュレーションするための回路
R_A～R_Dの4つの抵抗でセンター・タップ付きの可変抵抗器を表現している．

　摺動子の位置を表すkを0.1から1まで0.1ステップで変化させて，周波数特性をシミュレーションします．kが0.5以下のときはR_A，R_Bの抵抗値は変化せず，kが0.5以上のときはR_C，R_Dの抵抗値が変化しないように「.paramコマンド」のif関数を使用してk1，k2という変数を設定しています．
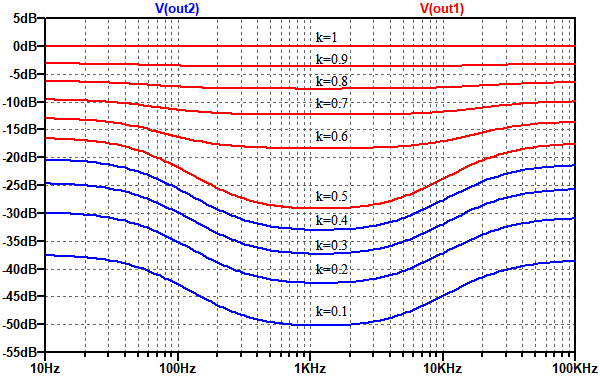
　そして，A15カーブの可変抵抗器となるよう，R_A～R_Dの抵抗値を「.paramコマンド」で計算しています．このような回路にすると，kが0～0.5までの周波数特性はOut2端子で，kが0.5～1までの周波数特性はOut1端子で確認することができます．
　図10は，図9のシミュレーション結果です．kの値が0.6以上ではほとんどフラットな周波数特性となっているのに対し，kが0.5以下では低域と高域が増強された周波数特性となっていることが分かります．