ひずみの基礎：2次高調波ひずみと3次高調波ひずみ

■問題

【ひずみ】

平賀　公久　Kimihisa Hiraga

　図1は，V₁の振幅が0.05V，周波数が100Hzのオーディオ信号を増幅してoutに出力するアンプの回路図です．このアンプのひずみの特性として「2次高調波ひずみが低く，3次高調波ひずみが高い」結果となりました．
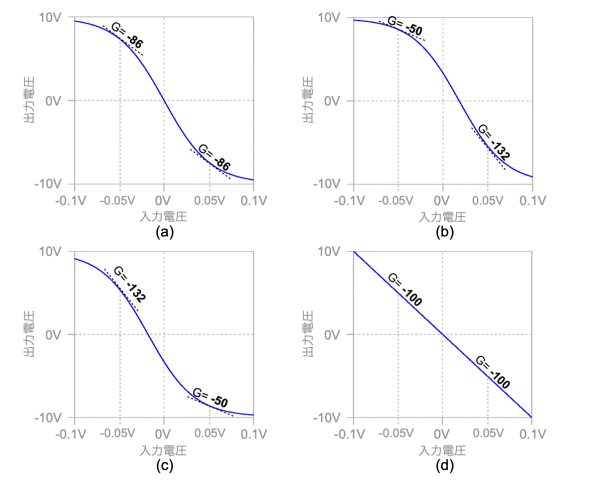
　図2の(a)～(d)は，アンプのひずみの入出力特性を示した図です．入出力特性に示したGの記号は，V₁の振幅が±0.05Vのときのアンプのゲインになります．
　そこで，図1のアンプの特性を示すのは，図2の(a)～(d)のどれでしょうか．

図1　V₁の信号を増幅してoutに出力するアンプ

図2　ひずみの入出力特性を示した図
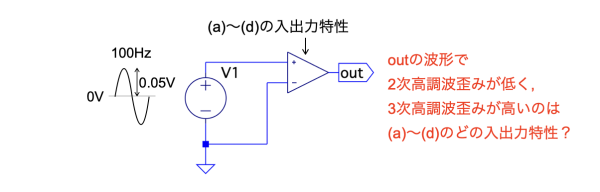
2次高調波ひずみが低く，3次高調波ひずみが高い入出力特性は？

(a)の入出力特性　 (b)の入出力特性　 (c)の入出力特性　 (d)の入出力特性

■ヒント

　アンプのひずみは，正弦波をアンプに入力し，アンプの出力信号が正弦波から異なる波形になるときに発生します．また，アンプのひずみは，入出力特性の非線形で発生します．そして，入出力特性の非線形を詳しくみると，信号の中点を境に非線形の曲線が対称または非対称かで，2次高調波ひずみと3次高調波ひずみが変わります．

■解答

(a)の入出力特性

　図2(d)は，入出力特性が線形なので，2次高調波ひずみと3次高調波ひずみは，発生しないので正解から外れます．
　3次高調波ひずみは，図2の(a)，(b)，(c)のような入力信号の正負の振幅を増幅する非線形の入出力特性で発生します．なので，違いは2次高調波ひずみとなります．
　入出力特性を詳しく検討すると，図2(a)は「入力振幅が±0.05VのときG=-86」と等しく，入力電圧の中点（0V）と入出力特性の交点を中心に180°プロットを回転すると同じになるので対称の特性になります．対称になる入出力特性は3次高調波ひずみが高く，2次高調波ひずみは無視できるほど低くなります．
　一方，図2(b)は「入力振幅が-0.05VのときG=-50，0.05VのときG=-132」，図2(c)は「入力振幅が-0.05VのときG=-132，0.05VのときG=-50」の特性です．図2(b)と図2(c)を180°プロットを回転すると同じにならず非対称の特性になります．非対称になる入出力特性は，2次高調波ひずみと3次高調波ひずみの両方を含み，2次高調波ひずみは図2(a)より高くなります．
　これにより，2次高調波ひずみが低く，3次高調波ひずみが高い入出力特性は図2(a)になります．

■解説

●ひずみは入出力特性の非線形で生まれる
　アンプのひずみは，入出力特性の非線形によって発生し，入力信号と出力信号の波形が異なります．アンプにひずみがあると，入力の波形と出力の波形は異なるので，聞こえ方が変わってしまいます．オーディオで使うアンプは，低ひずみが求められるので，ひずみに注意して回路設計を進めます．ひずみの評価は，アンプの出力信号をフーリエ変換して，入力の基本波以外にある高調波ひずみの有無や，そのレベルを用います．LTspiceでは，「.four」ステートメントを用いてアンプの出力信号をフーリエ変換し，高調波ひずみの成分を評価します．

●入出力特性の非線形には対称と非対称がある
　入出力特性の非線形について詳しくみると，入力信号の中点に対して対称と非対称があります．具体的に，対称とは入力電圧の中点（0V）と入出力特性の曲線の交点を中心に点対称（交点を中心に180°プロットを回転する）になることをいいます．このような入出力特性が対称のときは，3次高調波ひずみが発生し，続いて5次高調波ひずみ，7次高調波ひずみという具合に奇数次のひずみが主になります．
　逆に，非対称のときは，2次高調波ひずみが発生し，続いて4次高調波ひずみ，6次高調波ひずみという具合に偶数次のひずみが見えてきます．
　アンプのひずみの評価で，奇数次の高調波ひずみが主なときは，入出力特性全体の非線形を線形になるように改善をします．また，偶数次の高調波ひずみが主なときは入出力特性の非対称を対称になるように改善をします．このように高調波ひずみの成分を知ることで，回路の調整方法が異なってきます．
　今回は，2次高調波ひずみが顕著に表れる回路と3次高調波ひずみが顕著に表れる回路の2つを使い，その波形も用いながら，入出力特性とひずみの関係を解説します．その後，図2の(a)～(d)の入出力特性の2次高調波ひずみと3次高調波ひずみをシミュレーションで確認します．

●2次高調波ひずみが顕著に表れる回路
　2次高調波ひずみが顕著に表れる回路は，図3(d)の整流回路になります．この入出力特性を図3(a)に示します．図3(a)の入出力特性は，負側の入力信号を出力しますが，正側の入力信号は出力しない特性になり，入力信号の中点に対して非対称になります．
　図3(c)のV₁の振幅が1V，周波数が100Hzの入力信号を回路へ加えると，図3(a)の入出力特性により，図3(b)の出力波形になります．ここでは整流回路のoutの波形をフーリエ変換して高調波ひずみ成分を調べます．
　シミュレーションは，図3(d)の回路を「.tran 100m」の指定で0ms～100msの「.tran解析」を実行します．そして「.four 100Hz V(out)」の指定で，基本波が100Hzのoutのフーリエ変換も同時に実行しています．「.options plotwinsize=0」は，シミュレーションのデータ圧縮をOFFにする指定で，フーリエ変換の精度が悪化しないようにしています．

図3　2次高調波ひずみが発生する回路とその波形
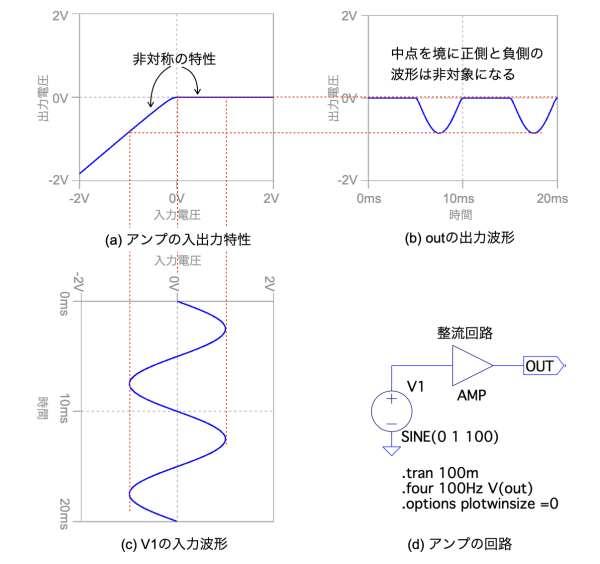
図3(c)のV₁の波形が図3(a)の入出力特性により図3(b)の波形になる．
図3(d)はアンプのシミュレーション回路．

　図4は，シミュレーション後に表示したフーリエ変換の結果になります．フーリエ変換の結果は，ログファイル中にあるので「Ctrl+L」（コントロールキーとLキーを同時押し）で表示します．図4のHarmonic Numberは1が基本波，2が2次高調波，3が3次高調波…となります．Fourier Componentがフーリエ変換の結果で，Normalized Componentが基本波のフーリエ変換の結果を1で正規化した値になります．ここではフーリエ変換後の大小関係をみたいので，Normalized Componentに注目します．
　図4の2次高調波と3次高調波を赤字で表しました．正規化した値をみると基本波の成分の1に対し，2次高調波は0.48，3次高調波は0.05になります．このように入出力特性が非線形で，かつ非対称のときはoutの波形は2次高調波が高くなり，3次高調波は低くなる特性になります．2次高調波等の偶数次高調波は，回路に整流性があるときに発生するひずみになります．

図4　図3(d)のoutについて基本波が100Hzでフーリエ変換した結果
正規化した2次高調波ひずみは0.48，3次高調波ひずみは0.05になる．

●3次高調波ひずみが顕著に表れる回路
　3次高調波ひずみが顕著に表れる回路は，図5(d)のクロスオーバーひずみを発生する回路になります．この入出力特性を図5(a)に示します．図5(a)の入出力特性は，入力信号の中点に対して対称になります．図5(c)のV₁の振幅が1V，周波数が100Hzの入力信号を回路へ加えると，図5(a)の入出力特性により，図5(b)の出力波形になります．

図5　3次高調波ひずみが発生する回路とその波形
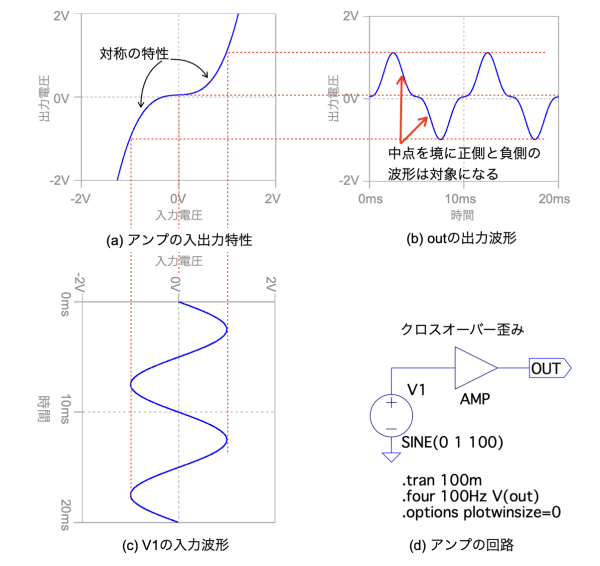
図5(c)のV₁の波形が図5(a)の入出力特性により図5(b)の波形になる．
図5(d)はアンプのシミュレーション回路．

　図6は，シミュレーション後に表示したフーリエ変換の結果になります．「.tran解析」とフーリエ変換の指定は図3(d)と同じです．図6の2次高調波と3次高調波の正規化した値をみると，基本波の成分の1に対し，2次高調波は0.009，3次高調波は0.31になります．このように入出力特性が非線形で，かつ対称のときは，outの波形は2次高調波が低くなり，3次高調波は高くなるのが分かります．

図6　図5(d)のoutについて基本波が100Hzでフーリエ変換した結果
正規化した2次高調波ひずみは0.009，3次高調波ひずみは0.31になる．

　次は，図2の(a)～(d)の入出力特性によるひずみをシミュレーションで確かめます．

●入力信号の中点に対して対称の特性の高調波ひずみ
　図7(d)は，図2(a)の入出力特性になる差動アンプになります．図7(a)の入出力特性は，図2(a)と同じで，入力信号の中点に対して対称の特性になります．差動アンプの出力は「out1-out2」の計算で求めます．

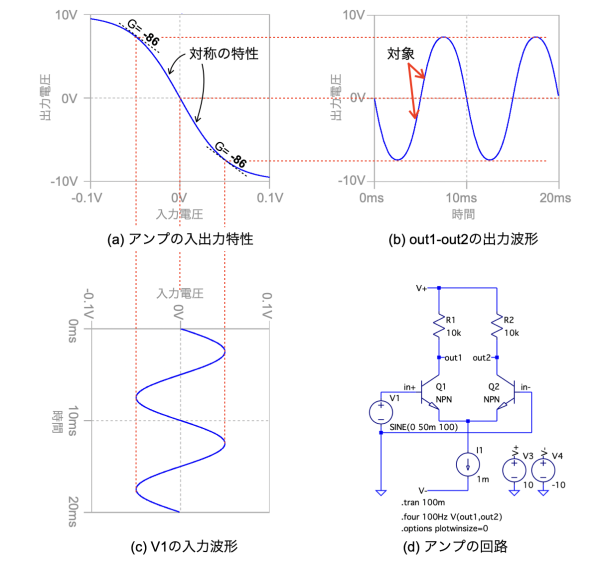
図7　図2(a)の入出力特性で発生するひずみを調べる回路とその波形
図7(c)のV₁の波形が図7(a)の入出力特性により図7(b)の波形になる．
図7(d)はアンプのシミュレーション回路．

　図8は，シミュレーション後に表示したフーリエ変換の結果になります．「.tran解析」とフーリエ変換の指定は図3(d)と同じです．図8の2次高調波と3次高調波の正規化した値をみると，基本波の成分の1に対し，2次高調波は0.0000005，3次高調波は0.06になります．このように入出力特性が対称のときは，outの波形は2次高調波が低くなり，3次高調波は高くなるのが分かります．

図8　図7(d)のout1-out2について基本波が100Hzでフーリエ変換した結果
正規化した2次高調波ひずみは0.0000005，3次高調波ひずみは0.06になる．

●入力信号の中点に対して非対称の特性の高調波ひずみ
▼図2(b)の入出力特性
　図9(d)は，図2(b)の入出力特性になる差動アンプになります．Q₁のNPNトランジスタが1個，Q₂のNPNトランジスタは「NPN 2」の指定で2個並列接続し，差動アンプのバランスを崩した回路になります．図9(a)の入出力特性は図2(b)と同じで，入力信号の中点に対して非対称の特性になります．差動アンプの出力は「out1-out2」の計算で求めます．

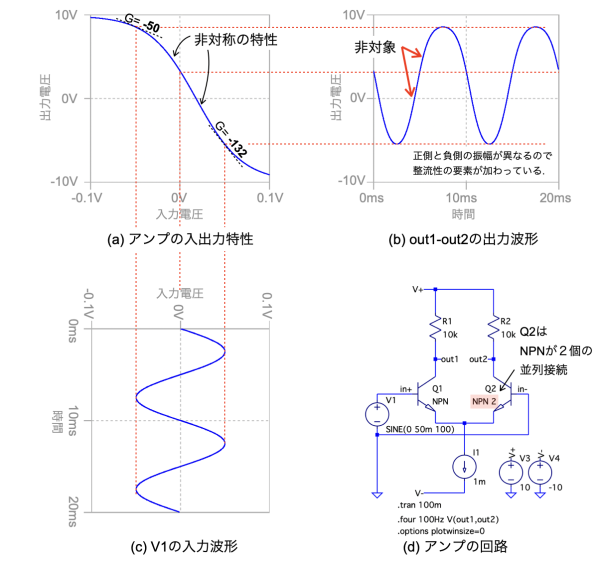
図9　図2(b)の入出力特性で発生するひずみを調べる回路とその波形
図9(c)のV₁の波形が図9(a)の入出力特性により図9(b)の波形になる．

　図10は，シミュレーション後に表示したフーリエ変換の結果になります．「.tran解析」とフーリエ変換の指定は図3(d)と同じです．図10の2次高調波と3次高調波の正規化した値をみると，基本波の成分の1に対し，2次高調波は0.12，3次高調波は0.05になります．2次高調波ひずみが加わるのは，差動アンプのバランスを崩したため，入出力特性が非対称になり，整流性の要素が加わることに因ります．

図10　図9(d)のout1-out2について基本波が100Hzでフーリエ変換した結果
正規化した2次高調波ひずみは0.12，3次高調波ひずみは0.05になる．

▼図2(c)の入出力特性
　図11(d)は，図2(c)の入出力特性になる差動アンプになります．Q₁のNPNトランジスタは「NPN 2」の指定で2個並列接続し，Q₂のNPNトランジスタが1個になので，先ほどの図9(d)のQ₁とQ₂が入れ替わった回路になります．

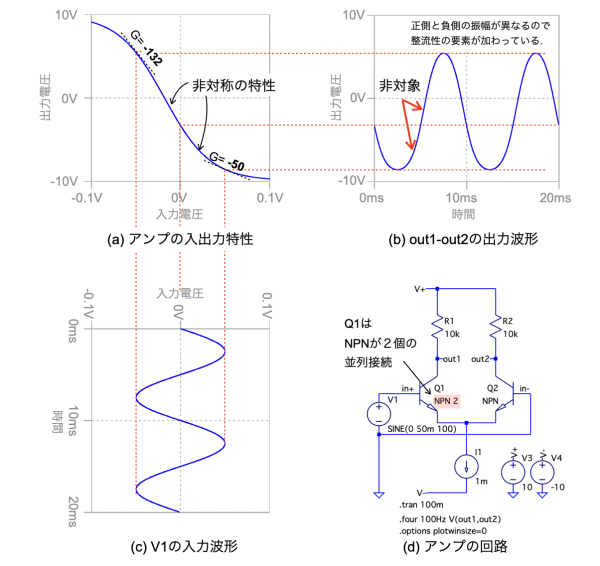
図11　図2(c)の入出力特性で発生するひずみを調べる回路とその波形
図11(c)のV₁の波形が図11(a)の入出力特性により図11(b)の波形になる．

　図12は，シミュレーション後に表示したフーリエ変換の結果になります．「.tran解析」とフーリエ変換の指定は図3(d)と同じです．図9(d)のQ₁とQ₂が入れ替わっただけなので，2次高調波と3次高調波の正規化した値は図10と同じになります．

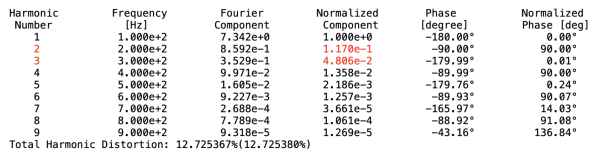
図12　図11(d)のout1-out2について基本波が100Hzでフーリエ変換した結果
正規化した2次高調波ひずみは0.12，3次高調波ひずみは0.05になる．

●入出力特性が線形になる理想アンプ
　図13(d)は，図2(d)の入出力特性になる理想アンプになります．図13(a)の入出力特性は図2(d)と同じで，入出力特性は線形になります．

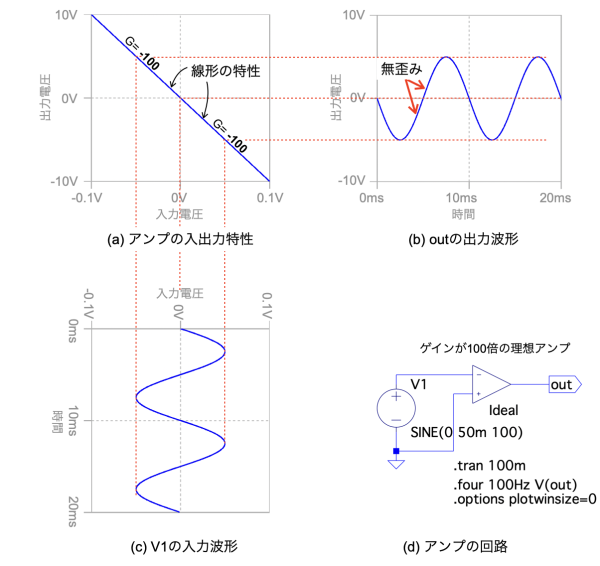
図13　図2(d)の入出力特性で発生するひずみを調べる回路とその波形
図13(c)のV₁の波形が図13(a)の入出力特性により図13(b)の波形になる．

　図14は，シミュレーション後に表示したフーリエ変換の結果になります．「.tran解析」とフーリエ変換の指定は図3(d)と同じです．図14の2次高調波と3次高調波の正規化した値をみると，基本波の成分の1に対し，2次高調波は0.00000016，3次高調波は0.00000016になります．このように入出力特性は線形なので，2次高調波と3次高調波は低くなり，outの波形はひずみません．

図14　図13(d)のoutについて基本波が100Hzでフーリエ変換した結果
正規化した2次高調波ひずみは0.00000016，3次高調波ひずみは0.00000016になる．

　以上，シミュレーションより，2次高調波ひずみが低く，3次高調波ひずみが高いのは，図2(a)になるのが分かります．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice9_018.zip

●データ・ファイル内容
Amp1_Tran.asc：図7(d)の回路
Amp1_Tran.plt：図7(d)のプロットを指定するファイル
Amp2_Tran.asc：図9(d)の回路
Amp2_Tran.plt：図9(d)のプロットを指定するファイル
Amp3_Tran.asc：図11(d)の回路
Amp3_Tran.plt：図11(d)のプロットを指定するファイル
Amp4_Tran.asc：図13(d)の回路
Amp4_Tran.plt：図13(d)のプロットを指定するファイル
Ideal_OP.asc：図13(d)の理想アンプ・サブサーキット
Ideal_OP.asy：図13(d)の理想アンプ・サブサーキットのシンボル