ボリューム・コントロールに使用される可変抵抗器の特性

図1(a)は,可変抵抗器のシンボルで,図1(a)の②(摺動子)を動かすことで,①-②間の抵抗値が変化します.図1(b)は,可変抵抗器の特性を示すグラフで,横軸が摺動子の位置で,縦軸が①-③間(全体の抵抗)と①-②間の抵抗比のグラフです.
可変抵抗器には,摺動子の位置と抵抗比の変化によって,図1(b)のような,AカーブとBカーブと呼ばれる特性があります.可変抵抗器のAカーブとBカーブの特性や用途の説明として正しいのは,(a)~(d)のどれでしょうか.
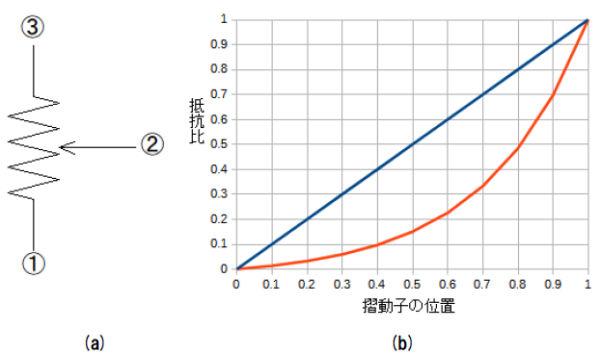
(a)可変抵抗器のシンボル
(b)可変抵抗器の特性を示すグラフ
(a) Aカーブは摺動子の位置に比例して直線的に抵抗比が変化する
(b) Bカーブは摺動子の位置に対して指数関数的に抵抗比が変化する
(c) Aカーブでゲイン調整した結果をdBで表すと直線的にコントロールできる範囲が広い
(d) Bカーブでゲイン調整した結果をdBで表すと直線的にコントロールできる範囲が広い

一般的に,電子回路の直流電圧調整には,Bカーブ特性の可変抵抗器が使われます.
Aカーブ[図1(b)の赤線]の可変抵抗器は,摺動子の位置に対して指数関数的に抵抗比が変化します.そのため,ゲイン調節に使用した場合,摺動子の位置の変化に対する減衰量の変化が対数的となり,減衰量をdBでプロットしたときに,直線的にコントロールできる減衰量の範囲が広くなります.
●可変抵抗器の構造と特性
ロータリ・タイプの可変抵抗器は,図2(a)のようにドーナツ状の抵抗体と,抵抗体に接触して回転する摺動子から構成されています.図2(b)のグラフの横軸は,摺動子を左[図2(a)の①側]に回し切ったときを0とし,右[図2(a)の③側]に回し切ったときを1としています.縦軸は,①-③間の抵抗と①-②間の抵抗比を表しています.
均一な抵抗値の抵抗体を使用したものは,図2(b)の青線のように,摺動子の回転角度に対し,直線的に抵抗比が変化します.このような特性のものをBカーブと呼んでいます.
一方,抵抗体の厚みを場所によって変えることにより,場所によって抵抗値を変えたものもあります.図2(b)の赤線のように,摺動子の回転角度に対して指数関数的に抵抗比が変わるものをAカーブと呼びます.
Aカーブの可変抵抗器にも,カーブの傾きによっていくつか種類があり,摺動子の位置が中央(0.5)のときの抵抗比(%)で特性を表しています.15Aという表記の場合,摺動子の位置が中央(0.5)のときの抵抗比が15%になるような特性となっています.
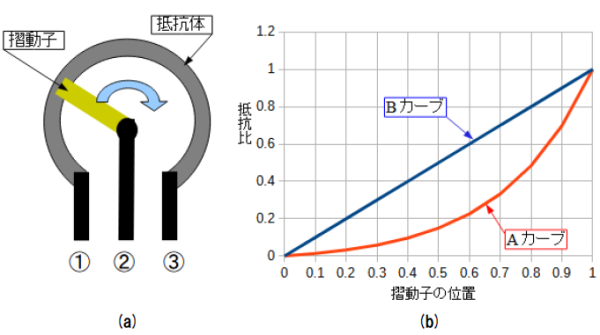
(a)可変抵抗器の構造の模式図
(b)可変抵抗器の抵抗値の変化特性
●AカーブとBカーブをシミュレーションするための設定
図3は,LTspiceで可変抵抗器をシミュレーションするための回路です.変数(k)が摺動子の位置を表し,変数(R)が最大抵抗値で,図3では「R=50kΩ」となっています.
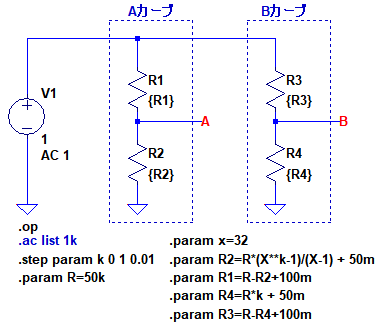
kという変数が摺動子の位置を表している.
まず,Bカーブの可変抵抗器から解説します.Bカーブの可変抵抗器は,R3とR4で構成しています.それぞれの抵抗値はR3,R4という変数を使用しています.「.paramコマンド」で,式1のようにR4の抵抗値を設定します.
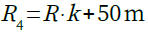 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)式2でR3の抵抗値を設定しています.R4とR3の抵抗値が0Ωや負の値にならないよう,式1に50mΩを,式2に100mΩを加算しています..
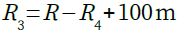 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)次にAカーブの可変抵抗器の等価回路を考えます.回路構成自体はBカーブのものと同じですが,摺動子の位置に対して指数的に抵抗比を変える必要があります.つまり,指数の底をXとし,抵抗比をRRとすると,式3のようになります.
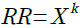 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)ここで,kが0のときは,RRも0となり,kが1のときはRRが1となるように,式3を式4のように補正します.
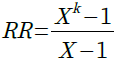 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)今回は,15Aの特性の可変抵抗器のモデルを作ります.そのためには,式5のように,kが0.5のときにRRが0.15となる必要があります.
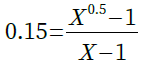 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)式5を満たすXを求めると,X≒32となります.そこで,図3ではX=32とし「.paramコマンド」を使用して,R2を式6のように設定します.
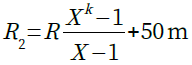 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)R1を式7で設定します.R4とR3と同じように,R2とR1の抵抗値が0Ωや負の値にならないよう,式6に50mΩを,式7に100mΩを加算しています..
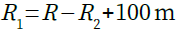 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)それぞれの可変抵抗器に1Vの電圧を加え,直流動作点解析を行います.そしてkという変数を0から1まで変化させたときのA,B端子の電圧をシミュレーションします.
●AカーブとBカーブの結果
図4が図3の可変抵抗器モデルのシミュレーション結果です.Bカーブの可変抵抗モデルは,摺動子の位置(k)に対して出力電圧が直線的に変化しており,抵抗比が直線的に変わっていることが分かります.
一方,Aカーブの可変抵抗モデルは,kの値に対して指数的に電圧が変化しています.そしてkが0.5のときには0.15Vとなっており,抵抗比が15%になっていることが分かります.
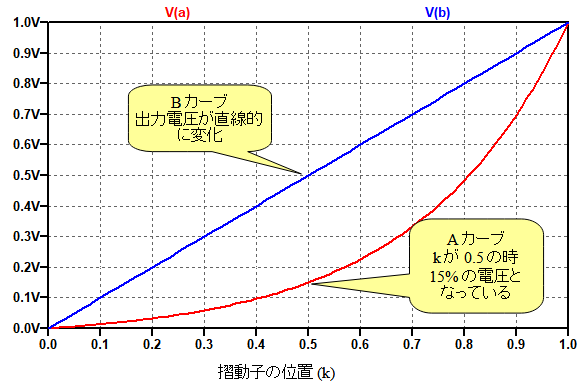
Aカーブの可変抵抗モデルは,kの値に値して指数的に電圧が変化している.
●ゲイン・コントロール特性を確認する
次に,AカーブとBカーブの可変抵抗器でゲイン調整を行った場合の特性を確認します.図2の回路の「.OPコマンド」をコメント化し,「.ac list 1k」をコマンドに戻します.そして,シミュレーションを実施した結果が,図5になります.縦軸が減衰量で,摺動子の位置に対する減衰量の変化のようすが確認できます.
Bカーブのモデルでは,kが0.3以上での減衰量の変化が少なく,0.3以下で急激にゲインが低下しています.一方,Aカーブのモデルでは,dBで表した減衰量が,直線的にコントロールできる範囲が広くなっています.
人間の音の大きさの感じ方は,音圧の対数に比例しているといわれています.そのため,Aカーブの可変抵抗を使用して音量調整を行うと,ボリュームの回転角度に対して,自然な音量変化が得られます.
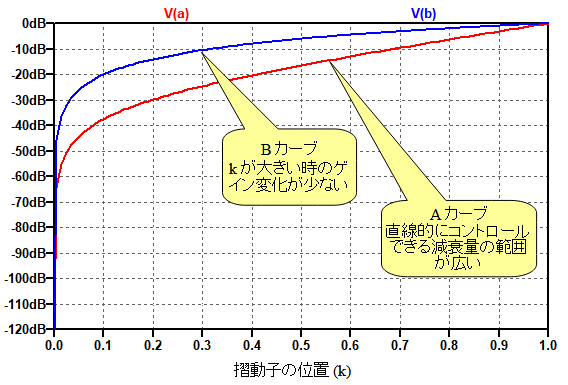
Aカーブのほうが,ゲインをdBで表すと直線的にコントロールできる減衰量の範囲が広い.
●Bカーブの特性をAカーブに近づける
Bカーブの可変抵抗器しか入手できない場合,抵抗を1本追加することでAカーブの特性に近づけることができます.図6がBカーブの可変抵抗器をAカーブの特性に近づけるための回路です.Bカーブの可変抵抗器の摺動子端子とGND間に抵抗R5が追加されています.
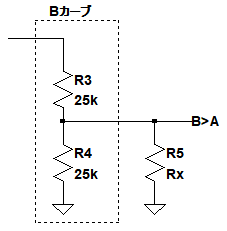
Bカーブの可変抵抗器の摺動子端子とGND間に抵抗R5が追加されている.
今回,R5の値は,kが0.5のときに抵抗比が15%となるように設定します.Bカーブの可変抵抗器で,kが0.5のときの抵抗比は50%となり,R3,R4ともに25kΩになります.この状態で抵抗比が15%となるR5の値(RX)を求めます.図6の抵抗比RRは式8のような式で表されます.式8をRXについて解くと「RX=5.35k」となります.ここではR5の値は,24シリーズの中から5.1kΩを選択します.
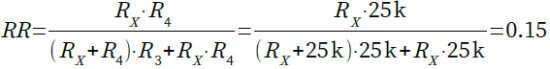 ・・・・・(8)
・・・・・(8)図7は,図3の回路にR5を追加したシミュレーション用の回路図です.Aカーブの特性と,Bカーブの可変抵抗器に抵抗を追加したものの差を検証します.
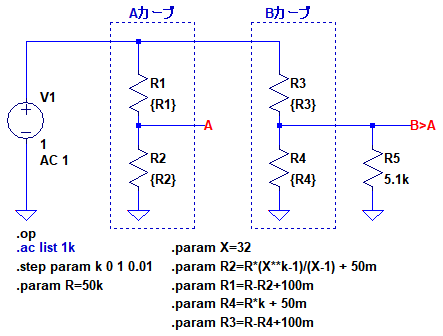
Bカーブの可変抵抗器の摺動子端子とGND間に抵抗R5を追加.
図8は,図7のシミュレーション結果です.Bカーブの可変抵抗器に抵抗を追加したものの特性は,Aカーブとある程度類似したものになっています.
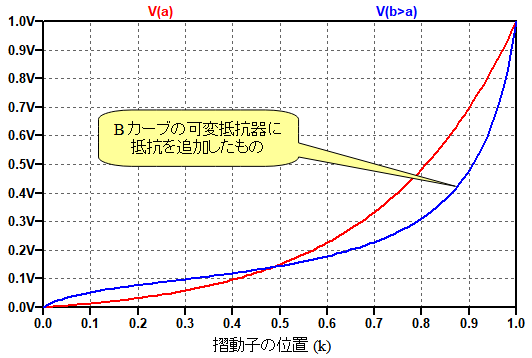
Bカーブの可変抵抗器に抵抗を追加した特性は,Aカーブとある程度類似している.
図9は,図7のBカーブの可変抵抗器に抵抗を追加した回路の,ボリューム・コントロール特性です.Bカーブの可変抵抗器に抵抗を追加したものは,kが大きい領域のゲイン変化がある程度大きくなっていますが,Aカーブほど自然ではありません.
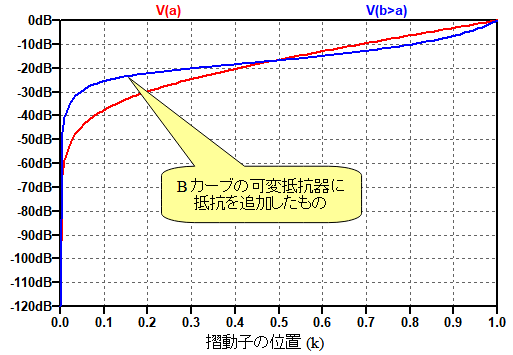
kが大きい領域のゲイン変化がある程度改善されるが,Aカーブ程,自然ではない.
以上,可変抵抗器のAカーブ,Bカーブについて解説しました.用途に合わせて,適切な特性の可変抵抗器を選択する必要があります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice9_017.zip
●データ・ファイル内容
VR_A_B_DC.asc:図3の回路
VR_A_B_AC.asc:図5をシミュレーションするための回路
VR_A_BA_DC.asc:図7の回路
VR_A_BA_AC.asc:図9をシミュレーションするための回路
■LTspice関連リンク先
(01) LTspice ダウンロード先
(02) LTspice Users Club
(03) LTspice メール・マガジン全アーカイブs
(04) ◆LTspice電子回路マラソン・アーカイブs
(05) ◆LTspiceアナログ電子回路入門アーカイブs
(06) ◆LTspice電源&アナログ回路入門アーカイブs
(07) ◆IoT時代のLTspiceアナログ回路入門アーカイブs
(08) ◆オームの法則から学ぶLTspiceアナログ回路入門アーカイブs
(09) ◆LTspiceエデュケーショナル・ファイルで学ぶアナログ回路アーカイブs
(10) ◆LTspiceドット・コマンドから学ぶアナログ回路アーカイブs
(11) ◆LTspiceで始める実用電子回路入門アーカイブs










