インバータを使用した発振回路

図1は,CMOSインバータを使用した発振回路です.電源電圧は5Vで,OUT端子に振幅5Vの矩形波が出力されます.回路構成は,抵抗(R1)が47kΩ,R2が470kΩ,コンデンサ(C1)が0.01μFとなっています.この回路の発振周波数に最も近いのは,(a)~(d)のどれでしょうか.
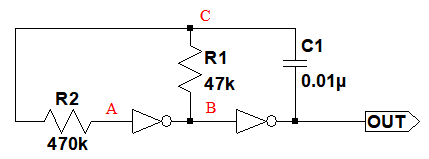
(a) 500Hz (b) 750Hz (c) 1kHz (d) 2kHz

R2は,CMOSインバータの破壊を防ぐためのものです.発振しているときにC点がどのような波形となるかということを考えれば,発振周波数を表す式を導くことができます.
R2は,破壊防止用でR1に比べて十分大きいので,発振周波数には影響がありません.この回路の発振周波数(fOSC)は,「fOSC=1/(2.2*R1*C1)」で計算することができます.図1の値を代入すると「fOSC=1/(2.2*47k*0.01μ)=967」となり,1番近いのは(c) 1kHzになります.
●発振のメカニズムを解析
図1のCMOSインバータを使用した発振回路が発振するメカニズムを,LTspiceで解析した結果を見ながら考えてみます.図2は,図1の回路に,実際のCMOSインバータICに内蔵されている素子を追加した回路図となります.図1の回路に,ダイオード(D1,D2)が追加されています.このダイオードは,CMOSインバータICに内蔵されている「保護ダイオード」と呼ばれるもので,静電気放電等により,IC内部のMOSトランジスタが破壊されるのを防ぐためのものです.
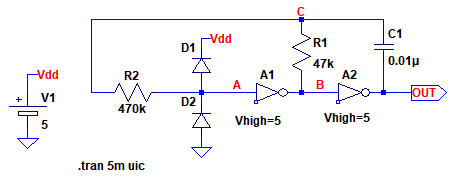
実際のCMOSインバータICに存在する保護ダイオード(D1,D2)が図1の回路に追加されている.
A1とA2は,LTspiceに内蔵されているインバータ(inv)です.電源電圧を5Vで使用したときと同じ動作にするため,シンボルを右クリックし,"Value"の欄に「Vhigh=5」と入力して,出力振幅を5Vに設定しています.
●充放電の繰り返しで発振が継続
図3は,図2のシミュレーション結果です.A点の波形はC点の波形の上下を制限したものになっています.これは,ダイオード(D1,D2)の働きによるものです.抵抗(R2)はダイオードに流れる電流を制限する働きをします.
解析開始直後にC点,A点の電圧は5VでB点の電圧は0Vになっています.B点の電圧が0Vなので,インバータ(A2)出力のOUT端子の電圧は5Vになっています.コンデンサ(C1)は,C点側が5Vに充電されています.しかし,R1によって放電していき,徐々に電圧が低下していきます.A点の電圧がインバータのしきい値電圧の2.5Vに達すると,B点の電圧は,5Vに変化します.すると,OUT端子の電圧は,0Vに急激に変化します.コンデンサ(C1)の両端の電圧差は,急激に変化しないため,C点の電圧は2.5Vから5V低下して-2.5Vになります.
コンデンサ(C1)のC点側は,-2.5Vになっています.今度は,R1によって充電されていき,徐々に電圧が上昇していきます.そして,C点の電圧が2.5Vに達するとA点の電圧も2.5Vになり,A1が反転して,B点の電圧は0Vになります.すると,OUT端子の電圧は,5Vに急激に変化し,その変化につられてC点の電圧は,2.5Vから5V上昇して7.5Vになります.その後再びR1で放電していく,という動作を繰り返すことで発振が継続することになります.
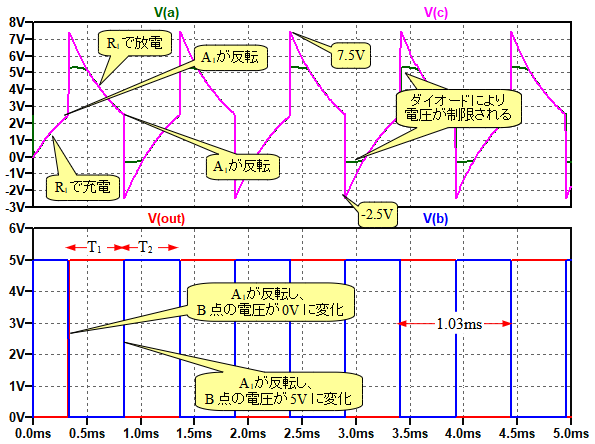
C1がR1で充放電されることを繰り返し発振が継続する.
●発振周波数の決まり方
次に,図3のシミュレーション結果をもとに,CMOSインバータを使用した発振回路の発振周波数がどのように決まるかを考えてみます.CMOSインバータの電源電圧をVddとすると,C点の電圧が1番小さいときの電圧は,「-Vdd/2」で,1番大きいときの電圧は1.5*Vddになります.
図3のT1の期間,C1は,「-Vdd/2」からVddに向かってR1で充電されていきます.ここで,初期状態でR1に加わる電圧は,「-Vdd/2」とVddの電圧差の「1.5*Vdd」になります.また,T2の期間,C1は「1.5*Vdd」から0Vに向かってR1で放電されていきます.
●発振周波数を計算するための状態変化が発生しないカーブ
図4は,C1の充放電によるC点の電圧変化のカーブを表したものになります.実際の発振回路では「Vdd/2」に達した時点で状態が変化します.しかし,図4は,発振周波数を計算するために,発振せずに,状態の変化が発生しない場合を表しています.
図4の左のグラフで,C点の電圧が「Vdd/2」になるのは,C1が電圧差の2/3まで充電されたときです.C1が電圧差の2/3まで充電するのに必要な時間がT1になります.また,図4の右のグラフでC点の電圧が「Vdd/2」になるのは,C1が初期電圧から2/3放電したときになります.C1が初期電圧から2/3放電するのに必要な時間がT2になります.
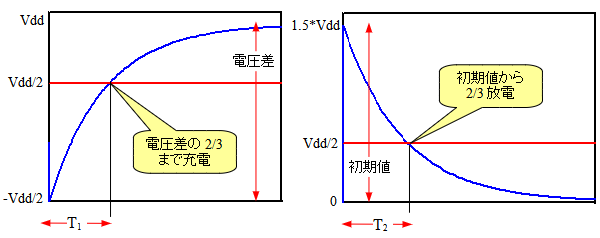
実際の回路では電圧が「Vdd/2」に達した時点で状態が変化する.
●発振周波数の計算
発振周波数を計算するため,まずT1を求めます.抵抗(R1)とコンデンサ(C1)の充電回路で,電圧差の何割まで充電されたかという比率をkとすると,kまで充電するのに必要な時間Tは式1で表されます.
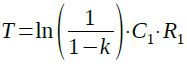 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
C点の電圧が「Vdd/2」になるのは,kが2/3のときなので,T1は式2のように「1.1*C1*R1」となります.
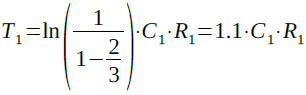 ・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・(2)
T2とT1は等しいため,発振周波数(fOSC)は式3で表されます.
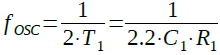 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3に図1の定数を代入すると,式4のように,約1khzとなります.
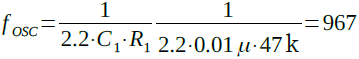 ・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・(4)
図3のシミュレーション結果,発振の1周期が1.03msとなっており,周波数は,970Hzと式4と同じになっています.式3にはVddの項がないため,この回路は,電源電圧による発振周波数の変化はありません.なお,R2の値がR1に比べて十分大きい場合,R2は,発振周波数に影響しません.
●NANDゲートを使用した発振回路
図5は,図1のインバータをNANDゲートに置き換えた発振回路です.LTspiceに内蔵されている「and」というロジック素子を使用しています.この素子は出力端子が2つあり,ANDとNANDの2つの機能を持っています.
また,入力端子が5つあり,最大,5入力NANDとして使用できます.図5の回路は,2入力NANDとして使用しています.なお,配線を接続しない端子は,自動的に未使用端子となり,存在しないものとして扱われます.V2は,発振をコントロールするための信号で,D点がハイレベルのときだけ発振します.図2では10msだけハイレベルにして発振させています.
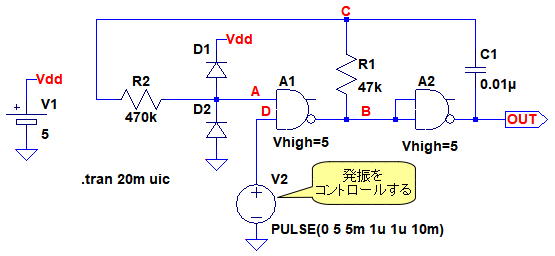
V2で発振をコントロールすることができる.
図6は,図5のシミュレーション結果です.D点の電圧が5Vのときだけ発振していることが分かります.
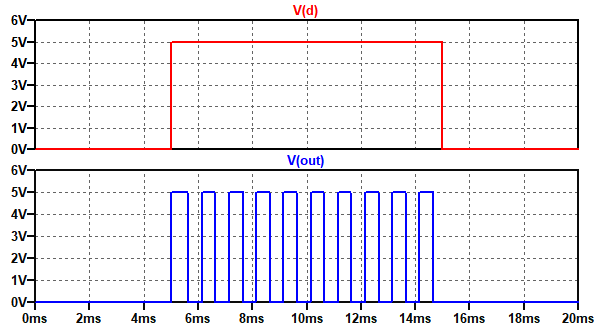
D点の電圧が5Vのときだけ発振している.
以上,インバータを使用した発振回路について解説しました.この発振回路は,電源電圧が変動しても発振周波数が変化せず,余ったゲート素子で作ることもできるため,電子工作などで広く使用されています.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice8_025.zip
●データ・ファイル内容
INV_OSC.asc:図2の回路
INV_OSC.plt:図3のグラフを描画するためのファイル
NAND_OSC.asc:図5の回路
■LTspice関連リンク先
(01) LTspice ダウンロード先
(02) LTspice Users Club
(03) LTspice メール・マガジン全アーカイブs
(04) ◆LTspice電子回路マラソン・アーカイブs
(05) ◆LTspiceアナログ電子回路入門アーカイブs
(06) ◆LTspice電源&アナログ回路入門アーカイブs
(07) ◆IoT時代のLTspiceアナログ回路入門アーカイブs
(08) ◆オームの法則から学ぶLTspiceアナログ回路入門アーカイブs
(09) ◆LTspiceエデュケーショナル・ファイルで学ぶアナログ回路アーカイブs
(10) ◆LTspiceドット・コマンドから学ぶアナログ回路アーカイブs










