シュミット・トリガを使用した発振回路

■問題

ディジタル回路

小川　敦　Atsushi Ogawa

　図1は，CMOSシュミット・トリガ・インバータを使用した発振回路です．電源電圧が5Vで，OUT端子には，振幅5Vの矩形波が出力されます．使用しているCMOSシュミット・トリガ・インバータは，出力がLow("L")になるしきい値電圧が3Vで，High("H")になるしきい値電圧が2Vとなっています．この回路の発振周波数に最も近いのは，(a)～(d)のどれでしょうか．

図1　シュミット・トリガ・インバータを使用した発振回路
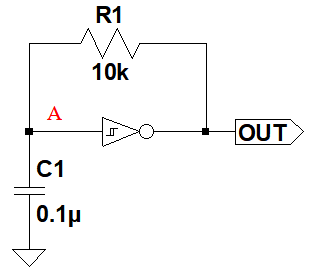
この回路の発振周波数は？

(a) 159Hz　(b) 318Hz　(c) 636Hz　(d) 1.23kHz

■ヒント

　まず，発振しているときのA点の電圧波形がどのようになるか考えます．その波形とR₁，C₁の関係から，発振周波数を計算することができます．このとき，R₁を定電流源に置き換えて近似計算すると，比較的簡単に求められます．

■解答

(d) 1.23kHz

　R₁を定電流源に置き換えると「発振周波数(f_OSC)=V_DD/(4*(V_TH-V_TL)*R₁*C₁)」と近似計算できます．
　ここで，シュミット・トリガ・インバータの出力が，"H"のときの電圧を「V_DD」，"H"から"L"となるしきい値電圧を「V_TH」，"L"から"H"となるしきい値電圧を「V_TL」とします．
　式に数値を代入すると，f_OSC=5/(4*(3-2)*1k*0.1μ)=12.5kとなり，(d)の1.23kHzが最も近い値となります．

■解説

●シュミット・トリガ・インバータの動作
　シュミット・トリガ・インバータは，しきい値電圧にヒステリシスを持っており，出力が，"L"となるしきい値電圧と"H"となるしきい値電圧が異なっています．
　図2は，LTspiceに内蔵されているシュミット・トリガ・インバータ(schmtinv)の特性をシミュレーションするための回路です．このシュミット・トリガ・インバータを使用するときは，シンボルを右クリックしてValueの欄に特性を指定するパラメータを記入します．
　図2中には，「Vhigh=5V Vt=2.5V Vh=0.5V Td=10n」と記入してあります．「Vhigh=5V」で出力振幅を指定し，「Vt=2.5V」でしきい値電圧の中央値を指定します．そして「Vh=0.5V」で中央値に対するヒステリシス幅を0.5Vと指定します．「Td=10n」は出力が変化するまでの遅延時間です．
　このように，指定することで，出力が"L"となるしきい値電圧が3Vで，"H"となるしきい値電圧が2Vになります．入力には，0Vから5Vに変化し，再び0Vになる信号を加えます．

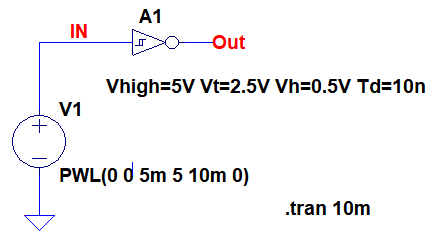
図2　シュミット・トリガ・インバータ(schmtinv)の特性をシミュレーションするための回路
Valueの欄に特性を指定するパラメータを記入する．

　図3は，シュミット・トリガ・インバータのシミュレーション結果です．出力が，"L"となるしきい値電圧は3Vで，"H"となるしきい値電圧が2Vになっていることが分かります．

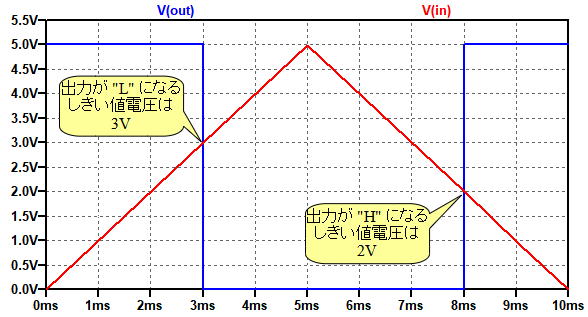
図3　シュミット・トリガ・インバータ(schmtinv)のシミュレーション結果

●シュミット・トリガ・インバータを使用した発振回路の動作
　図4は，シュミット・トリガ・インバータを使用した発振回路の等価回路図と出力波形です．シュミット・トリガ・インバータの出力が，"H"のときの電圧を「V_DD」，"H"から"L"となるしきい値電圧を「V_TH」，"L"から"H"となるしきい値電圧を「V_TL」とします．
　A点の電圧が0Vのとき，スイッチ(S₁)は電源(V₁)側に接続されています．すると，コンデンサ(C₁)は抵抗(R₁)によって充電され，A点の電圧は上昇していきます．　A点の電圧がV_TLになると，スイッチ(S₁)はGND側に接続されます．すると，C₁はR₁によって放電され，A点の電圧は減少していきます．A点の電圧がV_TLになるとS₁は再びV₁側に接続され，A点の電圧は上昇していきます．この動作を繰り返すことで発振が継続することになります．

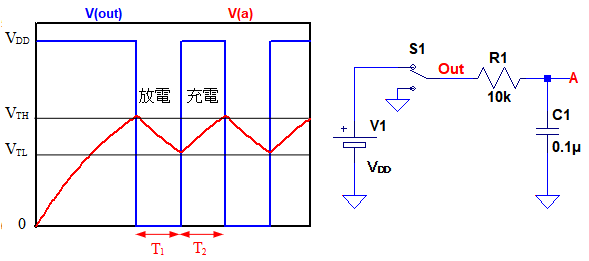
図4　シュミット・トリガ・インバータを使用した発振回路の等価回路図と波形

●発振回路の発振周波数の計算
　次に，この発振回路の発振周波数がいくつになるか計算してみます．最初にT₁を求めます．図4の放電期間のA点の電圧(V_A)は，時間をtとすると，式1で表すことができます．

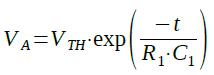・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　V_AがV_TLと等しくなったときの時間をT₁とすると，式1 は式2のように変形できます．

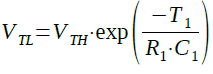・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　さらに式2は，式3のように変形することができます．

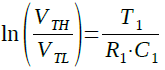・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3からT₁を求めると式4になります．

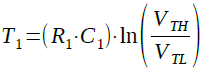・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　次にT₂を求めます．充電期間のA点の電圧の時間的変化は式5で表すことができます．

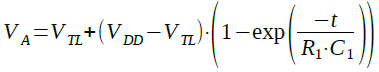・・・・・・・・・・・・・・・・・(5)

　V_AがV_THと等しくなったときの時間をT₂とすると，式5は式6のように変形できます．

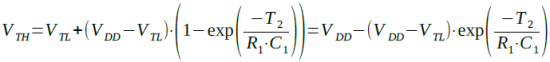・・・・・(6)

　さらに，式6は式7のように変形できます．

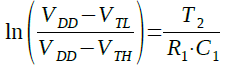・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式7からT₂を求めると，式8になります．

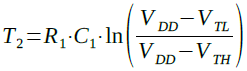・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　T₁とT₂（式4と式8）より，発振周波数(f_OSC)は式9のように計算できます．

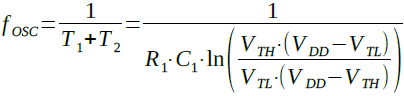・・・・・・・・・・・・・・・(9)

　図1の数値を当てはめると，発振周波数は式10 のように1.23kHzになります．

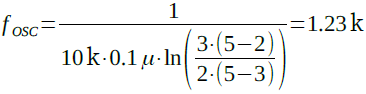・・・・・・・・・・・・・・・・・(10)

●「解答」で示した近似計算
　抵抗とコンデンサの充放電として計算すると上述のように，やや煩雑な計算が必要です．そこで，定電流源によるコンデンサの充放電に近似して考えると，「解答」で示した，もう少しシンプルな近似計算ができます．
　まず，抵抗にV_DD/2の電圧が印加されたときの電流を充放電電流(I_R)とします．I_Rは式11で計算できます．

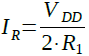・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　I_Rを使用すると，T₁，T₂は式11のように表わされます．

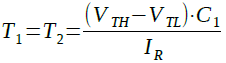・・・・・・・・・・・・・・・・・・・・・・・・・・(12)

　式11，式12より発振周波数を求めると，式13になります．

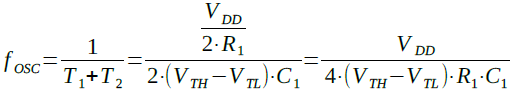・・・・・・・(13)

　図1の数値を代入して計算すると，式14のように1.25kHzとなり，近似計算でも式10に近い値が得られます．

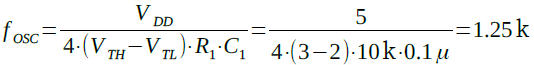・・・・・・(14)

●発振回路のシミュレーション
　図5は，図1のシュミット・トリガ・インバータを使用した発振回路をシミュレーションするための回路です．

図5　図1をシミュレーションするための回路

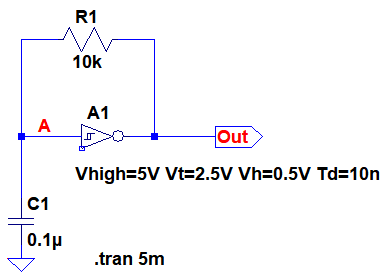
　図6が図5のシミュレーション結果です．A点の電圧の最大値は3Vで最小値は2Vとなっています．また1周期の時間は811μsとなっており，発振周波数は1.23kHzと式10で計算した値と同じになっています．

図6　図5のシミュレーション結果
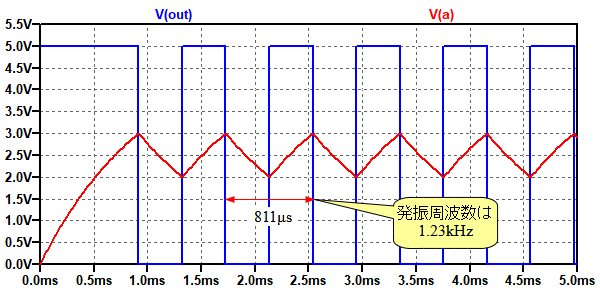
発振周波数は1.23kHzになっている．

　以上，シュミット・トリガ・インバータを使用した発振回路について解説しました．シュミット・トリガ・インバータを使用すると，非常に簡単にクロック信号を作ることができます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice8_023.zip

●データ・ファイル内容
Schmitt_INV.asc：図2の回路
Schmitt_INV.plt：図3のグラフを描画するためのPlot settinngsファイル
Schmitt_trigger_OSC.asc：図5の回路
Schmitt_trigger_OSC.plt：図6のグラフを描画するためのPlot settinngsファイル