微分回路の基本回路と実用的な回路

■問題
使用するコマンド ― .AC / .TRAN

平賀　公久　Kimihisa Hiraga

　図1は，OPアンプを使った基本的な微分回路です．V₁からOUTまでの周波数特性をAC解析で調べています．OPアンプは，図2の黒線で示した周波数特性があり，f_p1から高周波側では-20dB/dec（周波数が10倍あたり-20dBで減衰）の特性です．この条件のとき，OUTの周波数特性として正しいのは図2の(a)～(d)のどれでしょうか．

図1　基本的な微分回路
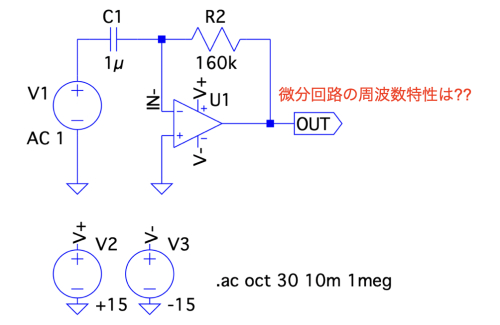
周波数特性をシミュレーションする．

図2　OUTの周波数特性
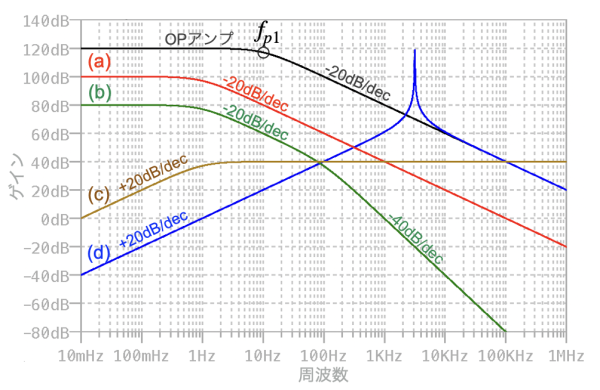
OUTの周波数特性で正しいのは，(a)～(d)のどれでしょうか？

(a)の周波数特性　(b)の周波数特性　(c)の周波数特性　(d)の周波数特性

■ヒント

　微分回路は周波数が変化するとゲインはどのようになるか，また，OPアンプとの周波数特性は微分回路にどのように影響するかを検討すると分かります．

■解答

(d)の周波数特性

　図1の微分回路のゲインを調べると式1になります．式1右辺のマイナス符号は，出力の位相が反転することを表します．

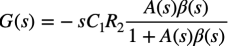・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　ここで，式1のA(s)β(s)はループ・ゲインです．内訳は，A(s)はOPアンプのオープン・ループ・ゲインで，β(s)は，式2のC₁とR₂による帰還率です．

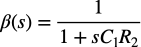・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　微分回路のゲインの周波数特性を調べるため，低周波における式1のゲインについて検討します．ラプラス演算子のsを「s=jω」へ置き換え，ループ・ゲインが1より十分大きく「A(jω)β(jω)=1+A(jω)β(jω)」とすると，式1は式3に近似できます．

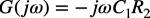・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3の絶対値がゲインなので，式4になります．

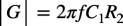・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4の「2π」と「C₁R₂」は定数ですので，低周波から徐々に周波数(f)が高くなると，ゲインも高くなります．具体的には，周波数が10倍高くなると(1decadeの変化あたり)，ゲインは10倍(+20dB)高くなります．このゲインの変化の割合は+20dB/decになり，図2の低周波帯で同じ変化になるのは(c)と(d)であり，(a)と(b)は消えます．
　次に周波数が1Hzでの具体的なゲインについて式4を使って求めると，「f=1Hz」,「C₁=1μF」,「R₂=160kΩ」より，「G=1」になります．デジベルに直すと「G=0dB」であり，このゲインになるのは(d)になります．
　また，違う検討として，100kHzより高周波帯の周波数特性からも(d)であることが分かります．具体的には，微分回路は負帰還回路ですので，高周波帯でOPアンプのオープン・ループ・ゲインより大きなゲインにはなりません．(c)は100kHz以上でOPアンプのオープン・ループ・ゲインより大きなゲインですので，(c)の周波数特性ではなく，OPアンプの周波数特性に沿って変化する(d)ということになります．

■解説

●微分回路の用途と注意点
　微分回路(ハイパス・フィルタ)は，波形処理に使われます．例えば，矩形波を入力して立ち上がりと立ち下がりのエッジを検出したり，Sin波をCos波に変えたり，三角波を矩形波に変えたりします．また，微分回路は信号ラインに直列にコンデンサが入るので，広い周波数帯で見ると，直流を通過させない交流アンプの用途にも使います．注意点として，図1の基本的な微分回路には弱点があり，出力が発振しやすいことです．以下では，微分回路の弱点である発振について検討し，発振対策をした実用的な微分回路を紹介します．

●基本的な微分回路は発振に注意する
　まず，図1のシミュレーションをして，微分回路の周波数特性を調べて答え合わせをします．ドット・コマンドは「.ac oct 30 10m 1meg」を使います．これは，10mHzから1MHz間を周波数が2倍あたり30ステップの周波数掃引で小信号AC解析を実行するという意味になります．
　図3は，図1のシミュレーション結果です．V(out)のプロットが微分回路の周波数特性です．V(out)/V(in-)のプロットは，OPアンプの出力から入力を除算しているのでオープン・ループ・ゲインの周波数特性になります．式4で検討したように，微分回路は低周波から周波数が高くなると+20dB/decの変化でゲインが高くなります．この周波数帯が微分回路として動作します．更に周波数が高くなるとOPアンプのオープン・ループ・ゲインと同じになります．この周波数特性は(d)になります．

図3　基本的な微分回路の周波数特性をプロット
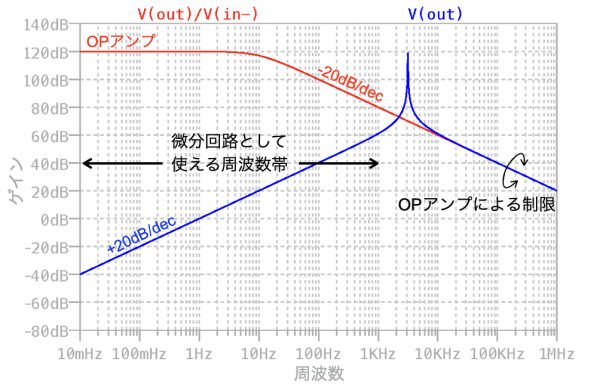
約1kHzより低周波側が微分回路として使える．

　次に,図4の回路で微分回路のトランジェント解析をし，OUTの波形を確認します．図4は，図1と同じですが，V₁が異なっており以下のように指定しています．

PWL REPEAT FOREVER (0 -0.5 500m 0.5 1 -0.5) ENDREPEAT

　PWLは，Piece-wise Linearの略で，電圧源の時間的な電圧変化を折線で指定するものです．具体的に，V₁は0秒で-0.5V，0.5秒で0.5V，1秒で-0.5Vの折線で表した三角波を最後まで繰り返すという意味になります．そして「.tran 5」は0秒?5秒間のトランジェント解析を実行します．

図4　トランジェント解析をする回路
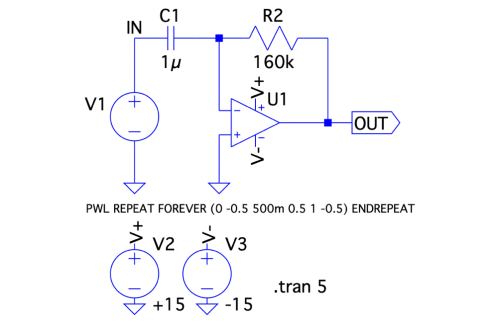
入力は振幅が±0.5V，周波数が1Hzの三角波．

　図5は，トランジェント解析をしたINの電圧とOUTの電圧のプロットです．三角波[V(in)]を微分すると矩形波[V(out)]になります．しかし，三角波の頂点付近で，OUTは，約3kHzで発振する区間があります．このように基本的な微分回路は，負帰還が不安定になって発振する弱点があります．

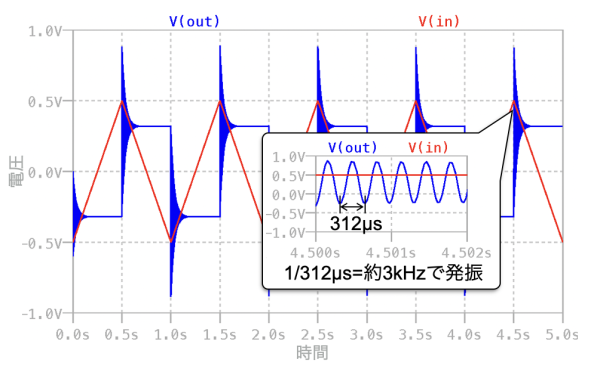
図5　トランジェント解析のプロットに，拡大したプロット図を加えた図
OUTは約3kHzで発振している．

●発振する微分回路
　発振する原因は，微分回路のループ・ゲインの検討から分かります．図6は，図1のループ・ゲインを調べる回路です．ループ・ゲインは，負帰還を一巡するゲインのことで，具体的には図1のOUTとR₂間を切り離して，図6のようにV₁の位置を変更します．このようにするとV₁からOUTまでの負帰還を一巡するループ・ゲインが分かります．OPアンプに入力オフセット電圧や入力バイアス電流，そして，入力オフセット電流がある場合，図6の方法ではOUTが飽和して正しいシミュレーションができないので，Middle Brook法等で試してください．Middle Brook法の解説については，過去の「真のループ・ゲインを求める」を参考にしてください．

図6　微分回路のループ・ゲインを調べる回路

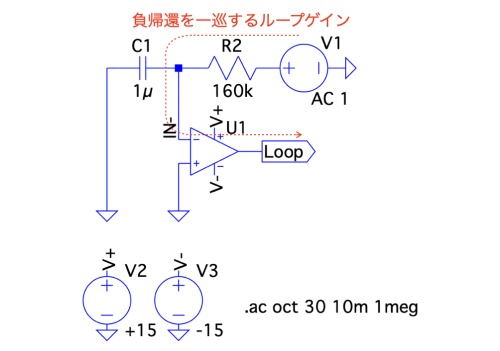
　図7は，図6のシミュレーション結果です．上段がOPアンプのオープン・ループ・ゲインと帰還率（V₁からIN-までの減衰率）のプロットで，下段がループ・ゲインのプロットです．下段のループ・ゲインは，上段の2つの周波数特性の和になります．OPアンプのオープン・ループ・ゲインと帰還率の2つは，-20dB/decの傾きで減衰するので，ループ・ゲインは10Hz以上の周波数で-40dB/decになり，位相も180°変化します．
　この特性により，ループ・ゲインが0dBのときの位相余裕は0°になって正帰還となり，不安定（発振する）になります．位相余裕は0°のときの周波数は3.2kHzであり，図5の発振周波数とほぼ同じになります．このように基本的な微分回路は，回路の構成上，負帰還が不安定になります．

図7　上段はOPアンプと帰還率の周波数特性
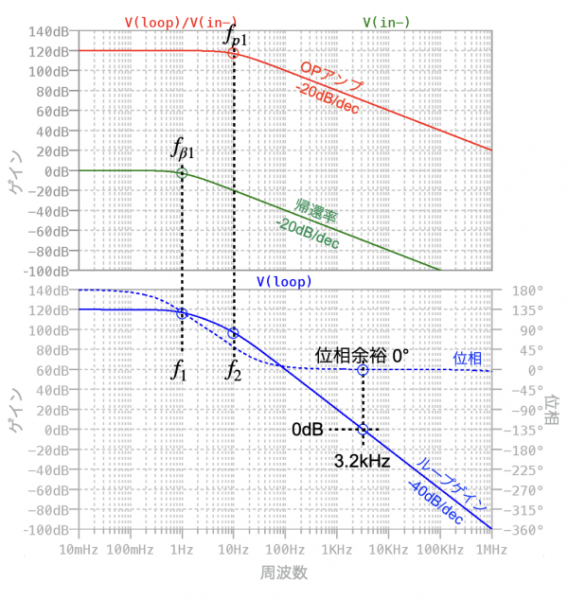
下段がループゲインと位相の周波数特性．ループ・ゲインは，位相余裕がゼロで負帰還は不安定であるのが分かる．

●発振しない実用的な微分回路
　図8は，図1にR₁とC₂を加えた実用的な微分回路になります．回路定数は発振を対策するため，C₁R₁＞C₂R₂，R₂＞R₁の関係にします．まず,この回路のV₁からOUTまでの周波数特性を検討します．

図8　実用的な微分回路
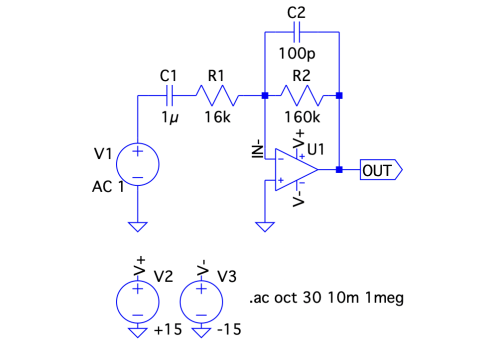
図1の回路にR₁とC₂を追加している．

　図8の微分回路のゲインを調べると式5になります．式5と式1を比べると，微分に関係するsC₁R₂の項に(1+sC₁R₁)と(1+sC₂R₂)が加わります．

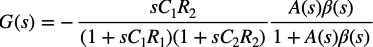・・・・・・・・・・・・・・・・・(5)

　式5のsC₁R₂の項は，式1～式4の検討と同じように，式6の1Hzの周波数で微分回路のゲインは0dBになります．

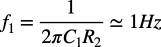・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　(1+sC₁R₁)の項は，発振対策に関係するもので，式7の周波数になります．発振対策の詳細は後述します．

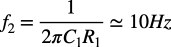・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　(1+sC₂R₂)の項は，高域側の周波数特性を決めます．具体的には図1ではOPアンプのオープン・ループ・ゲインの周波数特性で決まった高域側の帯域を，C₂とR₂で帯域制限します．図8のときは式8の10kHzが高域側の帯域となります．

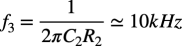・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　式7と式8の周波数間のゲインは，式9の反転アンプのゲインになります．

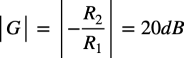・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　図9は，図8のシミュレーション結果です．実用的な微分回路の周波数特性とOPアンプのオープン・ループ・ゲインをプロットしました．先程の検討の通り，微分回路のゲインは式6の周波数で0dBになります．式7と式8の周波数間のゲインは式9の20dBになります．そして高域側の帯域は式8の10kHzで制限されます．図3の基本的な微分回路の周波数特性と比べると，微分回路として使える周波数帯は狭くなりますが，OPアンプの周波数特性の影響を受けない回路になります．

図9　実用的な微分回路の周波数特性
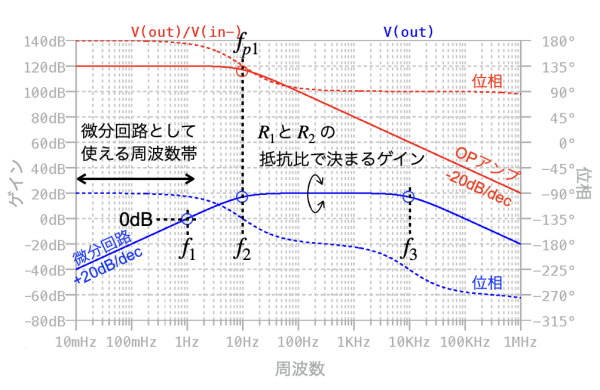
実線がゲイン，波線が位相．微分回路として使える周波数帯は狭くなる．

●OUTの発振を止める
　図10は，図8の実用的な微分回路のループ・ゲインを調べる回路です．図6のときと同じように，OUTとR₂C₂間を切り離してV₁の位置を変更します．この回路をシミュレーションして位相余裕を調べます．

図10　実用的な微分回路のループ・ゲインを調べる回路

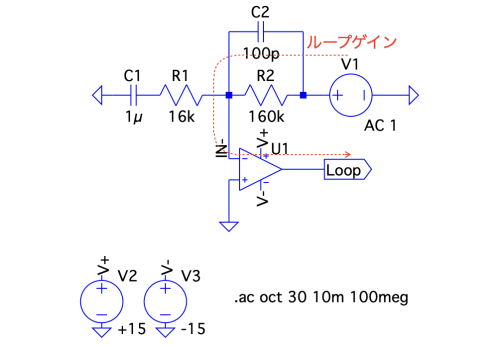
　図11は，図10のシミュレーション結果です．上段がOPアンプのオープン・ループ・ゲインと帰還率のプロットで，下段がループ・ゲインのプロットです．図7の基本的な微分回路のループ・ゲインのシミュレーションと比べると，帰還率の周波数特性を変更しています．具体的には，OPアンプが持つ「f_p1=10Hz」の周波数と式7のf₂の周波数を同じにして，10Hz以上の周波数でループ・ゲインが-40dB/decにならないようにしています．この対策により位相余裕は45°になり，図7の0°から改善して負帰還は安定になります．

図11　図10のシミュレーション結果
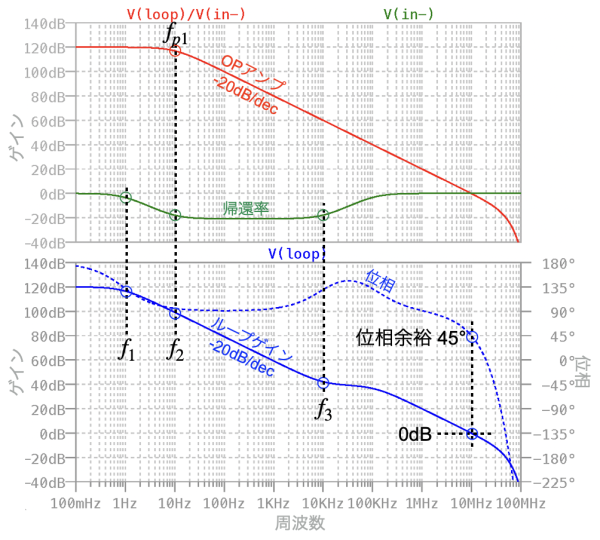
上段がOPアンプと帰還率の周波数特性，下段がループゲインと位相の周波数特性．
位相余裕は45°になり改善している．

　図12は，実用的な微分回路のトランジェント解析でOUTの波形を調べ，発振するかどうかを確かめる回路です．三角波のPWLの設定は図4と同じです．

図12　実用的な微分回路のトランジェント解析をする回路

　図13は，図12のトランジェント解析のINの電圧とOUTの電圧をプロットしました．図5の基本的な微分回路と比べると，OUTの発振は無くなることが分かります．

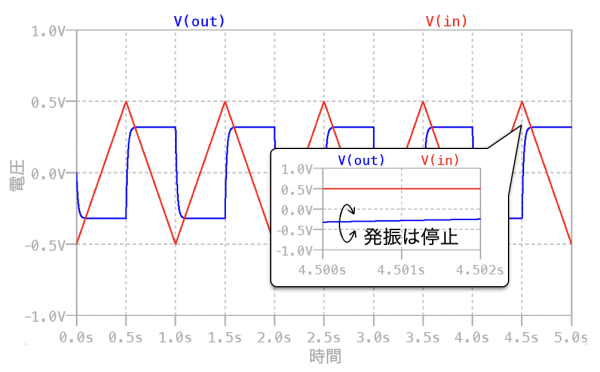
図13　図12のINとOUTの波形をプロットした図に，拡大したプロット図を加えた図
OUTは発振していない．

　以上，基本的な微分回路はOUTが発振することがあります．この対策として実用的な微分回路が用いられています．実用的な微分回路はACアンプの特性になり，図9のf₂とf₃間の周波数を増幅する用途にも使われます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_036.zip

●データ・ファイル内容
inverting_differentiator AC.asc：図1の回路
inverting_differentiator AC.plt：図1のプロットを指定するファイル
inverting_differentiator Tran.asc：図4の回路
inverting_differentiator Tran.plt：図4のプロットを指定するファイル
inverting_differentiator Loop.asc：図6の回路
inverting_differentiator Loop.plt：図6のプロットを指定するファイル
practical_differentiator AC.asc：図8の回路
practical_differentiator AC.plt：図8のプロットを指定するファイル
practical_differentiator Loop.asc：図10の回路
practical_differentiator Loop.plt：図10のプロットを指定するファイル
practical_differentiator Tran.asc：図12の回路
practical_differentiator Tran.plt：図12のプロットを指定するファイル