単一電源で使えるDeboo積分回路

■問題
使用するコマンド ― .TRAN

平賀　公久　Kimihisa Hiraga

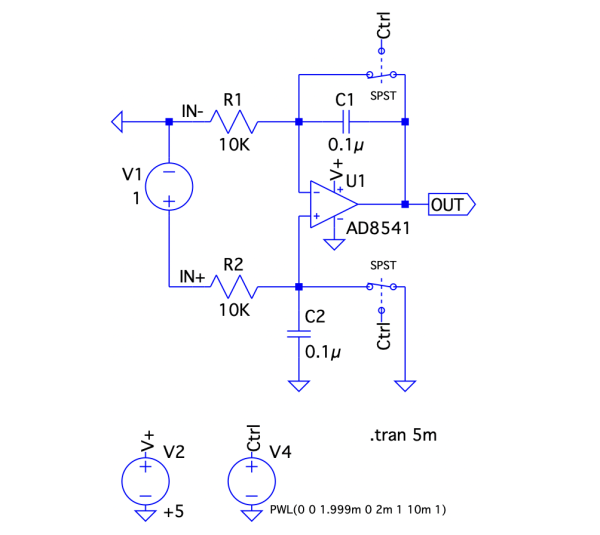
　図1は，電源が+5V単一電源で動作する積分回路です．回路内のスイッチは，0msから2ms未満ではGNDに接続，2msでスイッチが切り替わりR₄へ接続します．このようにスイッチが切り替わったときのOUTの波形として正しいのは図2の(a)～(d)のどれでしょうか．ただし，OPアンプは理想とします．

図1　+5V単一電源でOUTが0Vから正に積分する回路
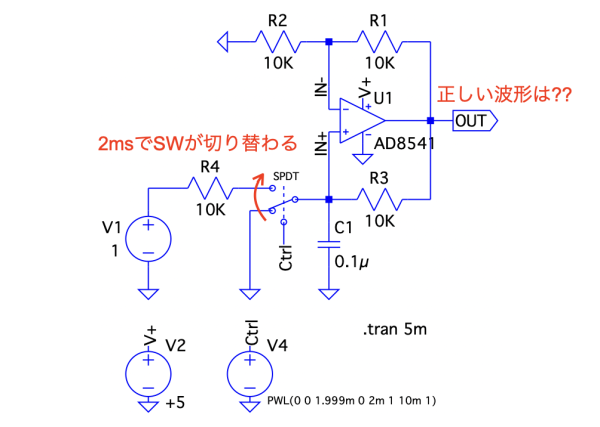
2ms後にスイッチが切り替わり，OUTの波形が変化する．

図2　OUTの波形

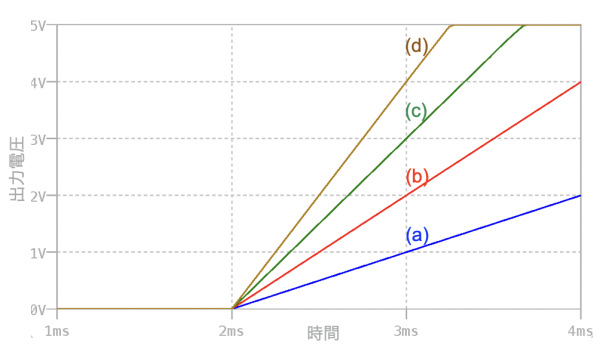
(a)の波形　(b)の波形　(c)の波形　(d)の波形

■ヒント

　図1は，ハウランド電流ポンプにスイッチと積分用のコンデンサをつけた回路です．ハウランド電流ポンプは，V₁の電圧と回路内の抵抗値で決まる電流でコンデンサを充電します．OUTの波形は，充電電流，コンデンサ値，時間，回路のゲインに関係します．この関係を調べて，プロットの値が読みやすい3msのOUTの電圧を検討すると分かります．図1は，単一電源で，0Vから正の積分出力を得られるDeboo積分回路と呼ばれています．

■解答

(b)の波形

　スイッチが2msでR₄に切り替わると，回路は，ハウランド電流ポンプとなり，コンデンサへ充電します．この充電電流は，式1になります．

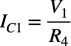・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　図1は「V₁=1V」，「R₄=10kΩ」なので，充電電流は「I_C₁=100μA」になります．コンデンサの充電電圧は，充電電流（I_C1），コンデンサ値（C₁），時間（T）で表すと式2になります．

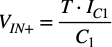・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　この充電電圧は，OPアンプの非反転端子の電圧（V_IN+）になります．コンデンサは「C₁=0.1μF」，充電電流は先程の「I_C1=100μA」，時間は図2のプロットでOUTの電圧が読みやすい3msとすると，充電している時間は「T=3ms-2ms=1ms」になります．これを式2へ入れると，「V_IN+=1V」になります．
　OUTの電圧は，V_IN+の電圧を非反転アンプのゲイン「G=1+R₁/R₂」で増幅した電圧なので式3になります．

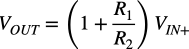・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　「R₁=R₂=10kΩ」なので回路のゲインは「G=2」となり，先程の「V_IN+=1V」を使うと，3msのOUTの電圧は「VOUT=2V」になります．この電圧になるのは(b)の波形になります．

■解説

●単一電源で0Vから正の積分出力を作るのは意外と難しい
　図3は，+5V単一電源で正の積分出力を作るときの要求事項を書き出したものです．単一電源とは，回路に1つの電源しかないことで，図3(a)では+5Vの電源のみになります．この電源で1つのOPアンプと，スイッチ，抵抗，コンデンサを使って回路を作り，図3(b)のように0V（GNDを基準）から正の積分出力を得るのが目標です．
　単一電源にすると，OPアンプの電源もその電圧になります．OPアンプを使った回路は，中点電圧を用いるものが多く，+5Vでは半分の+2.5V等になります．OPアンプの出力は，中点電圧を中心に信号が振れるので，0Vから正の積分出力を作るのは意外と難しいことになります．
　以降では，OPアンプを使った積分回路の基本型と，0Vから正の積分出力を得る差動積分回路を解説します．差動積分回路は扱いにくいところもあるので，1つの解決策としてDeboo積分回路が用いられることを解説します．

図3　+5V単一電源で0Vから正側へ充電する回路を作る
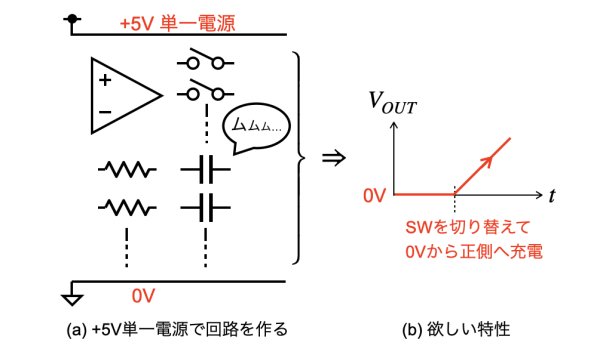
(a)回路で使える電源と部品　(b)出力で欲しい特性

●OPアンプを使った積分回路の基本型
　図4は，OPアンプを使った積分回路の基本型になります．この回路の電源は，検討しやすい±2.5Vの両電源で解説します．両電源では，回路の中点電圧はGND（=0V）にできます．スイッチが閉じているときはバーチャル・グラウンドの電圧がOUTの電圧になり，スイッチが開くとコンデンサへ電流が流れ，OUTの積分した電圧は負側になります．

図4　両電源（±2.5V）を使った積分回路の基本型

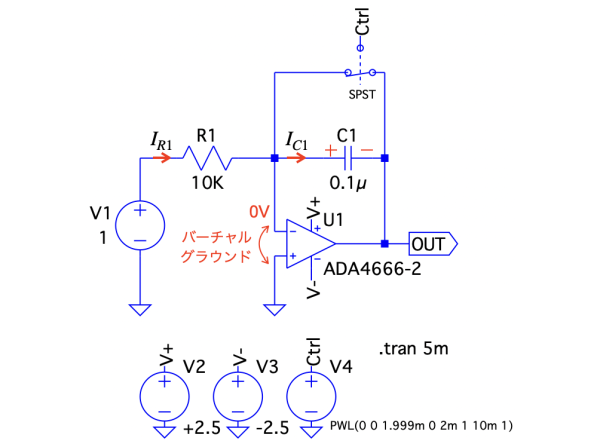
　図4の回路記号を使って，スイッチが開いた時の積分を机上計算で確かめます．スイッチが開くと，抵抗の電流とコンデンサの電流は等しくなり，式4になります．

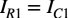・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4の抵抗の電流はオームの法則を使い，コンデンサの電流は電極の電荷変化を使って書き直すと式5になります．

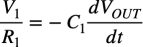・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5より，OUTの電圧に書き直して積分すると式6になります．

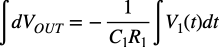・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式6を0～T秒で積分すると式7になります．このようにOUTの時間変化は，マイナスの符号がついた「-1/C₁R₁」のゲインに比例した積分出力になります．ここで，VOUT(0)はスイッチが閉じているときのOUTの電圧なので，図4ではバーチャル・グラウンドの0Vになり，スイッチが開くとOUTの電圧は0Vから負側へ振れる積分出力になります．

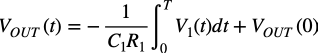・・・・・・・・・・・・・・・・・・・・・(7)

　具体的な値として，スイッチが開いて1ms経過後のOUTの電圧は，式7と図4の回路定数より，式8の-1Vになります．
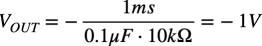・・・・・・・・・・・・・・・・・・・・・・・・・(8)

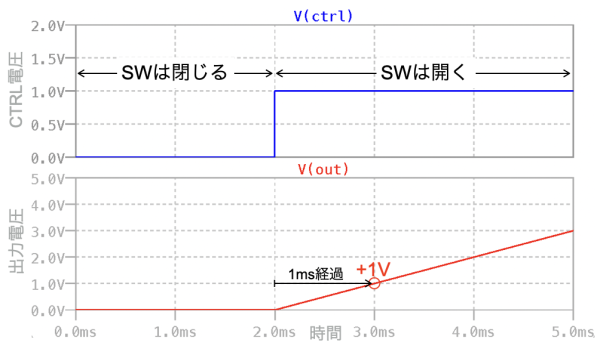
　図5は，図4をシミュレーションした結果です．使用したドット・コマンドは「.tran 5m」です．これは0ms～5ms間のトランジェント解析を実行するという意味になります．上段は，スイッチのコントロール電圧で，0Vは，スイッチが閉じている状態です．また，1Vは，スイッチが開いている状態を表します．下段は，OUTの電圧でスイッチが閉じている0ms～2ms未満のとき，0V，その後，2msからスイッチが開くと積分が始まり，2msから1ms経過した3msでは-1Vになり，式8の机上計算と一致することが分かります．
　以上のように，図4のOPアンプを使った積分回路の基本型は,負帰還にコンデンサが入るので，OPアンプの中点電圧に対して負側へ積分する回路になります．　図4は，±2.5Vの両電源なので，これを+5Vの単一電源にすると，図4の「V+を+5V」，「V-をGND」，「GNDを+2.5Vの中点電圧」のように電圧をシフトすれば同じになります．この場合，積分出力は，中点電圧+2.5Vから0Vに向かって積分する出力になり，図3(b)で示した0V（GNDを基準）から正の積分出力にはなりません．

図5　図3のスイッチの状態とOUTの電圧をプロット
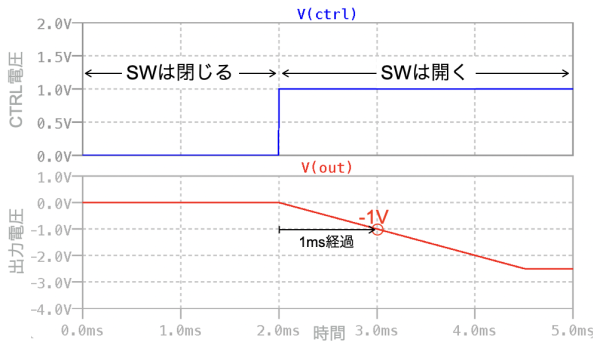
スイッチが開いて1ms後は-1Vになる．

●差動積分回路で正の積分出力を得る
　単一電源で0V（GNDを基準）から正の積分出力を得る回路として，図6の差動積分回路があります．差動積分回路は積分のゲインを同じにするため，式9のように回路定数を選びます．

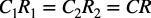・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　差動積分回路は，IN+の電圧をV_IN+，IN-の電圧をVIN-とすると，「V_IN+-VIN-」の差動信号を積分した出力になり，式10になります．

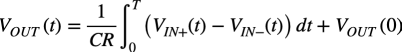・・・・・・・・・・・・・・・(10)

　式10のVOUT(0)は，2つのスイッチが閉じているときのOUTの電圧であり，バーチャル・グラウンドの0Vになります．2つのスイッチが開くと，OUTの時間変化は正の符号がついた「1/CR」のゲインに比例した積分出力になるので，0Vから正の積分出力を得る回路になります．具体的な値として，2つのスイッチが開いて1ms経過後のOUTの電圧は，式10と図6の回路定数より，式11の+1Vになります．

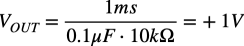・・・・・・・・・・・・・・・・・・・・・・・・・(11)

図6　差動積分を使った回路
R₁C₁=R₂C2の回路定数にする．

　図7は，図6をシミュレーションした結果です．使用したドット・コマンドは，図4と同じです．上段はスイッチのコントロール電圧です．0Vは，2つのスイッチが閉じている状態です．1Vは，2つのスイッチが開いている状態を表します．
　下段は，OUTの電圧で，2つのスイッチが閉じている0ms～2ms未満のとき0Vです．その後，2msから2つのスイッチが開くと積分が始まります．2msから1ms経過した3msでは，+1Vになり，式11の机上計算と一致することが分かります．
　しかし，差動積分回路は扱いにくい点があり，具体的には先程の式9に示した条件を満足するのが難しいことです．式9はコンデンサと抵抗で作る2つの時定数を合わせねばならず，抵抗は整合が良いものを入手できますが，コンデンサは難しいので，時定数を合わせるのが現実的ではありません．

図7　図6のスイッチの状態とOUTの電圧をプロットスイッチが開いて1ms後は+1Vになる

●Deboo積分回路で正の積分出力を得る
　単一電源で，0V（GNDを基準）から正の積分出力を得る回路は，図1に示した積分回路があります．この回路は考案者（G．J．Deboo）の名に因んでDeboo積分回路として知られています．Deboo積分回路は，ハウランド電流ポンプの抵抗を「R₁=R₂=R₃=R₄」にし，それにスイッチと積分用のコンデンサをつけた回路になります．図1ではスイッチがR₄に切り替わるとハウランド電流ポンプの電流源になり，負荷になるコンデンサへ充電します．ハウランド電流ポンプについては「LTspiceアナログ電子回路入門」の「ハウランド電流ポンプから負荷へ流れる電流はいくら？」で解説していますので，そちらを参照してください．
　図1のDeboo積分回路で，スイッチがGNDからR₄に切り替わったときのコンデンサの充電電圧（V_IN+）は，式12となります．式12のV_IN+(0)は，スイッチがGNDに接続しているときのV_IN+の電圧であり，グラウンドの0Vになります．

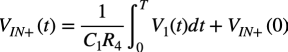・・・・・・・・・・・・・・・・・・・・・・(12)

　図1のOUTの電圧は，V_IN+の電圧を非反転アンプのゲイン「G=1+R₁/R₂」で増幅した電圧なので，式13になります．このようにスイッチがR₄に切り替わると式13の積分回路になります．OUTの時間変化は，正の符号がついた「(1+R₁/R₂)/C₁R₄」のゲインに比例した積分出力になるので，0Vから正の積分出力を得る回路になります．

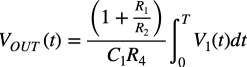・・・・・・・・・・・・・・・・・・・・・・・・・(13)

　具体的な値として，スイッチが開いて，1ms経過後のOUTの電圧は，式13と図1の回路定数より，式14の+2Vになります．

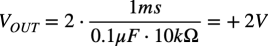・・・・・・・・・・・・・・・・・・・・・・・・(14)

　図8は，図1をシミュレーションした結果です．使用したドット・コマンドは，図4と同じです．上段はスイッチのコントロール電圧で，0VはGND側に接続した状態，1Vはスイッチが切り替わりR₄側へ接続した状態を表します．下段は，IN+の電圧とOUTの電圧です．スイッチがGND側に接続した0ms～2ms未満のときは，0Vです．その後，2msからスイッチがR₄側へ切り替わると積分が始まります．2msから1ms経過した3msではV_IN+の電圧が+1Vになり，OUTの電圧はその電圧を2倍した+2Vになるので，式14の机上計算と一致することが分かります．

図8　図1のスイッチの状態とIN+とOUTの電圧をプロット
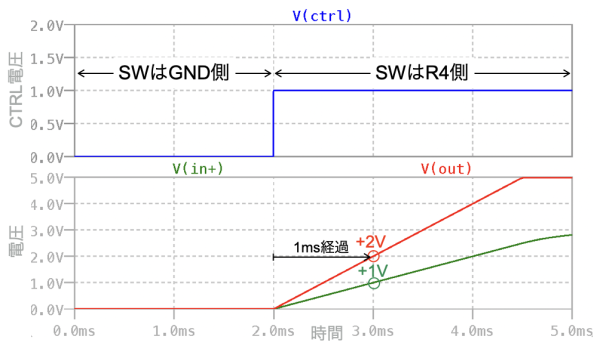
スイッチが開いて1ms後は+2Vになる．

　以上，単一電源で積分出力が0Vから正になる積分回路について解説しました．このような回路の用途は，リセット・スイッチでコンデンサを放電して，その後の充電時間を使ったタイマ回路などになります．なお，今回使用したOPアンプAD8541とADA4666は単電源動作ができ，入出力がレール・ツー・レール（電源からGNDまでスイングできる）になるCMOS OPアンプで，単一電源や低電源電流の用途で使います．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_034.zip

●データ・ファイル内容
deboo_integrator.asc：図1の回路
inverting_integrator.asc：図4の回路
inverting_integrator.plt：図5のプロットを指定するファイル
diffrential_integrator.asc：図6の回路
diffrential_integrator.plt：図7のプロットを指定するファイル
deboo_integrator.plt：図8のプロットを指定するファイル
SPDT.asc，SPDT.asy：2接点のスイッチの回路とシンボル
SPST.asc，SPST.asy：1接点のスイッチの回路とシンボル