無線通信に使用される90度位相シフト回路

■問題
使用するコマンド ― .AC，.step

小川　敦　Atsushi Ogawa

　図1は，ゲインが一定で，位相のみが変化する，オールパス・フィルタを2つ使用した，90度位相シフト回路です．in端子に信号を入力すると，Out1端子とOut2端子に，約90度位相のずれた信号が得られます．
　図1の回路で，Out1端子とOut2端子の信号の位相差が，90±10度となる，入力周波数範囲がもっとも広いR₁の値(Rx)は，(a)～(d)のどれでしょうか．

図1　オールパス・フィルタを2つ使用した，90度位相シフト回路
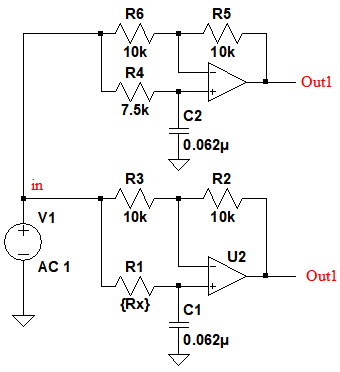
Out1とOutの位相差が90±10度となる，入力周波数範囲がもっとも広いR₁の抵抗値はいくつでしょうか．

(a)1kΩ　(b)2kΩ　(c)3.75kΩ　(d)15kΩ

■ヒント

　図1のオールパス・フィルタでは，入力と出力の位相差が，0度から180度まで周波数によって変化します．入力と出力の位相差が90度になる周波数は，R₁，C₁とR₄，C₂で決まります．ただし，1つのオールパス・フィルタでは，位相差が，90±10度の範囲は非常に狭くなります．そのため，時定数をずらしたオールパス・フィルタを二つ使用して，周波数範囲を広げます．2つのオールパス・フィルタの時定数を，どの程度ずらせば，90±10度の範囲が広くなるか，という観点で考えます．

■解答

(a)1kΩ

　Out1端子とOut2端子の信号の位相差が，90±10度となる入力周波数範囲がもっとも広くなるのは，R₁，C₁の時定数と，R₄，C₂の時定数の比が7.5になったときです．R₄は7.5kΩなので，時定数の比が7.5になるR₁の値は1kΩになります．そのため，正解は(a)です．また，時定数の比が4.5以下の場合は，位相差が80度以下になってしまいますので，(b)～(d)は不正解です．

■解説

●90度位相シフト回路の用途
　図2は，SSB(Single Side Band)と呼ばれる信号を生成するためのブロック図です．SSBは無線通信を行うための変調方式の1つで，通常の振幅変調の半分の周波数帯域で，音声信号を送信できるのが特徴です．
　図2のシステムでは，入力されたオーディオ信号の位相を90度シフトさせる必要がありますが，このとき使用されるのが，90度位相シフト回路になります．

図2　SSB信号を生成するためのブロック図
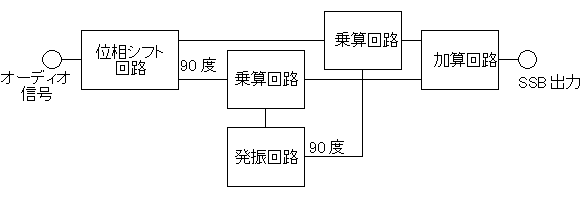
入力されたオーディオ信号を位相シフトして，2つの乗算器に加える

●オールパス・フィルタの特性
　図3は，OPアンプを使用したオールパス・フィルタです．この回路は，フィルタという名前がついていますが，すべての周波数でゲインは，1倍(0dB)です．

図3　OPアンプを使用したオールパス・フィルタ
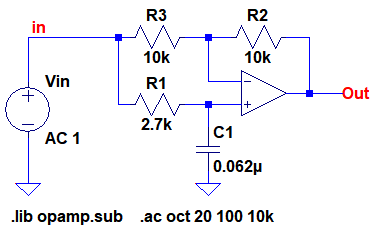
ゲイン一定で，位相は周波数によって0度から-180度まで変化する．

　ただし，位相は周波数によって0度から-180度まで変化します．そして位相が90度変化する周波数(f_C)は式1で計算することができます．

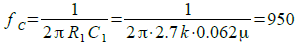・・・・・・・・・・・・・・・・・・・・・・(1)

　この回路の，周波数(f)に対する位相シフト量（θ）の絶対値は「T=R₁*C₁」とすると，式2で計算することができます．

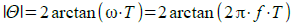・・・・・・・・・・・・・・・・・・・・・・(2)

　図4が，図3の周波数特性のシミュレーション結果です．ゲインは周波数が変わっても0dBで一定です．一方，位相は，周波数によって0度から-180度まで変化します．位相が90度±10度となる範囲は800Hz～1.15kとなっています．位相が90度となる周波数範囲が狭いので，この回路を図2の90度位相シフト回路として使用することはできません．

図4　オールパス・フィルタの周波数特性のシミュレーション結果
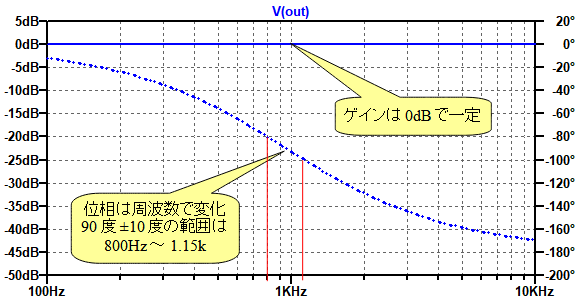
ゲイン一定で，位相は周波数によって0度から-180度まで変化する．

●90度位相シフト回路の特性
　図5は，2つのオールパス・フィルタを使用した90度位相シフト回路をシミュレーションするための回路図です．R₁の値は1kΩとなっています．周波数を100Hzから10kHzまで変えて，Out1とOut2の位相差がどのようになるか，シミュレーションで確認します．

図5　90度位相シフト回路をシミュレーションするための回路図
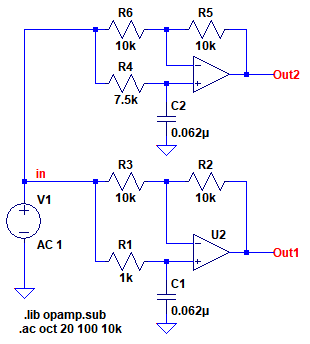
R₁の値は1kΩとなっている．

　図6は，図5の位相シフト回路のシミュレーション結果です．下段にOut1とOut2のゲインと位相を表示し，上段にOut1とOut2の位相差を表示しています．位相差を表示するとき，ph()という関数を使用しています．この関数は，引数の位相の絶対値を実数とし，虚数部を0とした複素数で結果を返します．そのため，グラフをプロットすると，ゲインと位相が表示され，ゲインの数値が位相を表します．また，位相軸は意味が無いので消去します．Out1の位相とOut2位相の差が90度±10度の範囲は，390Hz～2.25kHzと広くなっています．

図6　位相シフト回路のシミュレーション結果
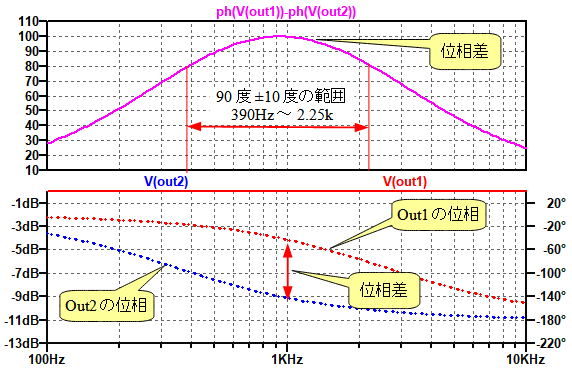
位相差が90度±10度の範囲は，390Hz～2.25kHzと広い．

　図6を見ると分かるように，Out1とOut2の位相差は，C₁，C₂の時定数とR₄，C₂の時定数の比によって大きさが変わります．また，位相差のグラフは，山なりのカーブになっています．
　次に，90度±10度の範囲を広くするためには，時定数の比をいくつにするのがよいかを考えてみます．時定数の比をkとすると，位相差(θd)は式2を使用し，式3のように求められます．

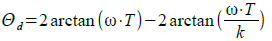・・・・・・・・・・・・・・・・・・・・・・・・(3)

　位相差の最大値を求めるため，式3をωで微分し，その値が0となるωを求めると，式4になります．これが，位相差が最大となる角周波数です．

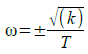・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4を式3に代入すると，式5になります．これが，位相差の最大値(Φ_max)になります．

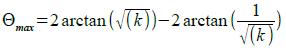・・・・・・・・・・・・・・・・・・・・・・・(5)

　表計算ソフトを使用して，式5のkを1から10まで変えたときの最大位相差（Φ_max)をプロットしたものが，図7になります．

図7　時定数比(k)と最大位相差のグラフ
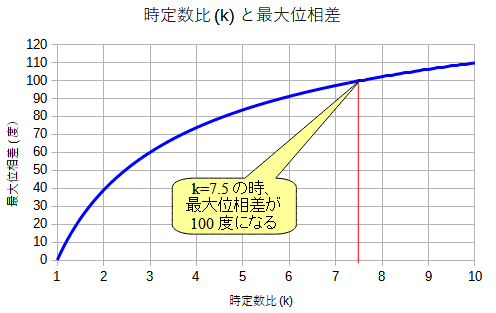
kを1から10まで変えたときの最大位相差をプロットしたもの．

　位相差が90度±10度の連続した周波数範囲が最大となるのは，最大位相差が100度のときです．そして，図7より，最大位相差が100度になるのはkが7.5のときだという事が分かります．また，kが4.5以下では，最大位相差が80度以下となってしまうことも分かります．

●90度位相シフト回路を「.step」で確認
　図8は「.step」コマンドを使用し，R₁の値を1kΩ，2kΩ，3.75kΩ，15kΩと変えて，周波数特性をシミュレーションするための回路です．

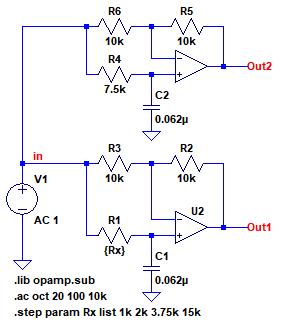
図8　R₁の値を変えて，周波数特性をシミュレーションするための回路
「.step」コマンドを使用し，1kΩ，2kΩ，3.75kΩ，15kΩと変化させる．

　図9は，図8のシミュレーション結果です．上段がOut1とOut2の位相差ですが，90度±10度となる，連続した周波数範囲が1番広いのはR₁が1kΩのときであるという事が分かります．

図9　R₁の値を変えたときのシミュレーション結果
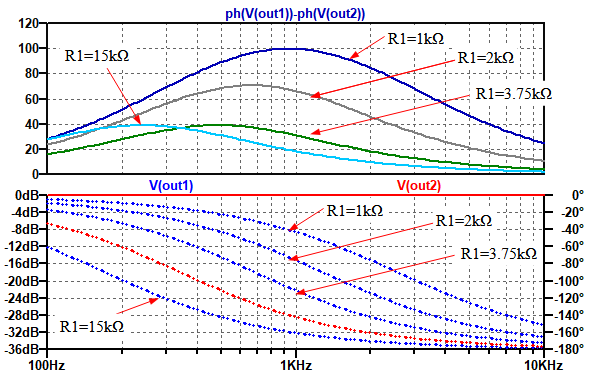
90度±10度となる，連続した周波数範囲が1番広いのはR₁が1kΩのとき．

　以上，90度位相シフト回路について解説しました．さらに，周波数範囲の広い90度位相シフト回路が必要な場合は，図1の回路を縦続接続し，適切な定数設定を行うことで，周波数範囲をさらに広くすることもできます．また，オールパス・フィルタの詳しい解説は「LTspiceアナログ電子回路入門：一次移相回路の最大の位相シフトは何度？」を参照してください．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_031.zip

●データ・ファイル内容
AllPass.asc：図3の回路
Phase_Shift.asc：図5の回路
Phase_ShiftA.plt：図6のグラフを描画するためのPlot settinngsファイル
Phase_Shift_step.asc：図5の回路
Phase_Shift_step.plt：図6のグラフを描画するためのPlot settinngsファイル