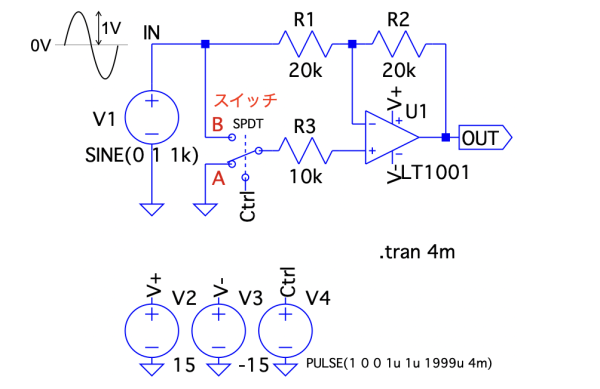
スイッチで位相を反転/非反転にする回路

■問題
使用するコマンド ― .TRAN/.STEP

平賀　公久　Kimihisa Hiraga

　図1は，スイッチの切り替えで，OUTの位相が反転/非反転になる回路です．図2の(a)～(d)は，スイッチがA側のときとB側のときのOUTの波形をプロットしました．この中からA側とB側の両方の波形が正しいのは，図2の(a)～(d)のどれでしょうか．
　ただし，検討を簡単にするため，スイッチのオン抵抗はゼロ，オフ抵抗は無限大，OPアンプは理想とします．

図1　2接点のスイッチでOUTの位相が変わる回路

図2　スイッチがA側とB側のときのOUTのプロット
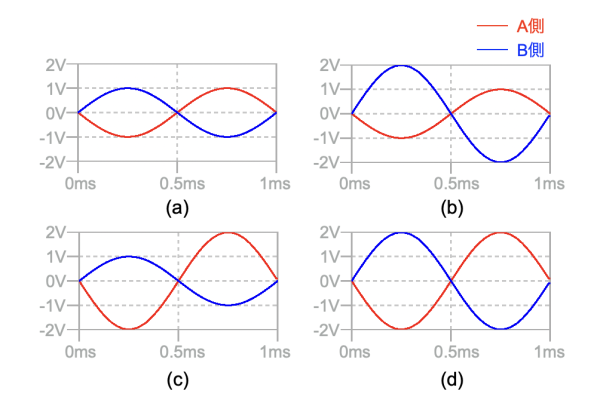
A側とB側の両方の波形が正しいのはどれ？

(a)の波形　(b)の波形　(c)の波形　(d)の波形

■ヒント

　図1は，スイッチがA側のときは反転アンプ，B側のときは非反転アンプになります．入力は振幅が1Vの正弦波です．A側とB側のときのゲインを検討して，OUTの位相と振幅がどうなるかを調べると分かります．

■解答

(a)の波形

　まず，スイッチがA側のときの赤色の波形について検討します．スイッチがA側のときはR₃の左側がGNDになるので，図1は反転アンプになります．このときのゲインは「G=-R₂/R₁」であり，R₁とR₂の抵抗は同じであることから「G=-1」になります．ゲインのマイナスの符号は位相が反転することを意味します．そして入力信号は，1Vでゲインの絶対値は1倍なのでOUTの振幅は1Vになります．これよりOUTの波形は，時間が0sからスタートすると，振幅は負側から始まる1Vの正弦波になります．この波形になっているのは図2の(a)と(b)であり,(c)と(d)は消えます．
　次にスイッチがB側のときの青色の波形について検討します．スイッチがB側のときは，R₃の左側がV1の入力信号と等しくなります．OPアンプの反転端子は非反転端子とバーチャル・ショートになるのでR₁の両端の電圧は同じV1の電圧になります．抵抗の両端の電圧差がゼロなのでR₁には電流が流れず，見かけ上の抵抗値は無限大になります．無限大の抵抗は回路に無いことと同じですから，R₁を回路から消すと「G=+1」の非反転アンプ，言い換えるとボルテージ・ホロワ回路になります．ゲインのプラスの符号は位相が非反転であることを意味します．そして入力信号は1Vでゲインの絶対値は1倍なのでOUTの振幅は1Vになります．これよりOUTの波形は時間が0sからスタートすると，振幅は正側から始まる1Vの正弦波になります．この波形になるのは，図2の(a)になります．
　このように，図1はスイッチの切り替えで位相が反転/非反転になり，そのときの振幅は入力信号と等しくなる回路として動作します．

■解説

●机上計算でゲインを詳しく調べる
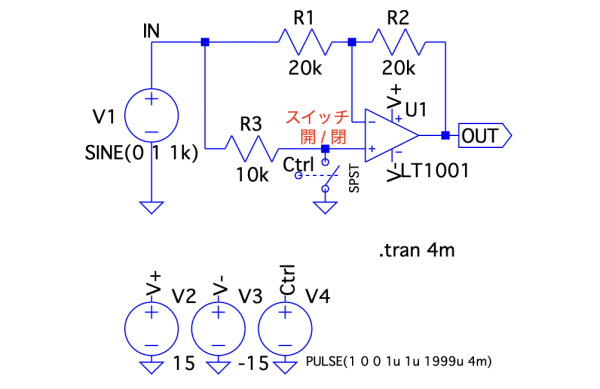
　ここでは図1の回路について，スイッチを切り替えたときのゲインを机上計算で詳しく調べます．図3は，図1のスイッチをA側とB側の状態について分けて表しました．まず図3(a)のスイッチがA側のときの回路のゲインを計算します．

図3　A側とB側の2つの状態を分けて表した回路

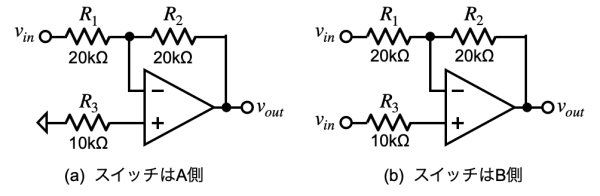
　図3(a)のスイッチがA側のときは，よく知られている反転アンプになります．入力電圧をv_in，出力電圧をv_out，R₁とR₂の抵抗値は等しいので，入力電圧と出力電圧の関係は式1になります．

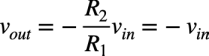・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　式1より，回路のゲインは，式2になります．ゲインの符号がマイナスで絶対値が1ですので，出力信号は位相が反転し，振幅は入力信号と同じになることが分かります．

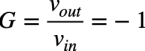・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　次に，図3(b)のスイッチがB側のときの回路のゲインを計算します．スイッチがB側の場合，R₁とR₃の左側の電圧は同じ入力電圧のv_inになります．図3(b)を重ね合わせの理を使って解析します．具体的には2つの入力電圧のうち，1つの入力電圧を残し，他の入力電圧をGNDとショートして各々回路解析します．そしてその結果を重ねる(解を加え合わせる)ことにより求まります．　R₁の左側のv_inを回路に残し，R₃の左側はGNDにしたときの出力電圧をv_out1とすると，反転アンプになります．R₁とR₂の抵抗値は等しいので,入力電圧と出力電圧の関係は式3になります．

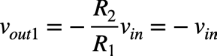・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　同じようにR₃の左側のv_inを回路に残し，R₁の左側はGNDにしたときの出力電圧をv_out2とすると，非反転アンプになります．R₁とR₂の抵抗値は等しいので,入力電圧と出力電圧の関係は式4になります．

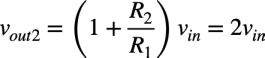・・・・・・・・・・・・・・・・・・・・・・・・(4)

　重ね合わせの理より，式3と式4を加え合わせると，図3(b)の入力電圧と出力電圧の関係は式5になります．

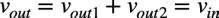・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5より，回路のゲインは式6になります．ゲインの符号がプラスで絶対値が1ですので，出力信号の位相は非反転で，振幅は入力信号と同じになることが分かります．

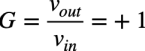・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　このように，図3の机上計算からもスイッチがA側のときのゲインは式2，B側のときのゲインは式6になり，スイッチの切り替えで位相が反転/非反転し，振幅は入力信号と同じになるのが分かります．

●シミュレーションで波形を確認する
　図1の2接点のスイッチは，V₄の電圧で切り替わるようにしています．具体的にはV₄の電圧がCtrlラベルの電圧となり，Ctrlが0VになるとA側に接続し，Ctrlが1VになるとB側に接続するようにしています．スイッチの切り替えはV₄の振幅を0V→1Vの矩形波にすることで2つのスイッチの状態を1回のシミュレーションで調べます．使用したドット・コマンドは「.TRAN」です．「.TRAN 4m」は時間が0sから始まり，4msまでのトランジェント解析を実行するという意味になります．
　図4は，図1の回路をシミュレーションした結果をプロットしました．　上段はCtrlの電圧で0s～2ms間は0VでスイッチはA側の状態，2ms～4ms間は1VでスイッチはB側の状態になります．中段は入力信号，下段は出力信号です．0s～2ms間のスイッチがA側のときは，図4中段の入力信号と図4下段の出力信号は位相が反転して振幅は1Vになることが分かります．同じように2ms～4ms間のスイッチがB側のときは，位相は非反転で振幅は1Vになることが分かります．

図4　図1をシミュレーション結果
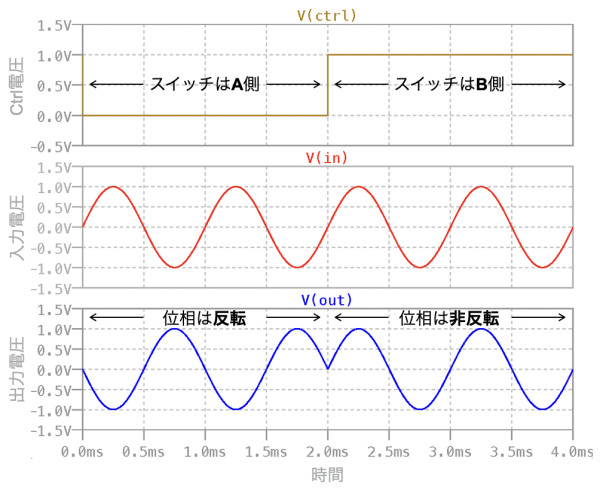
A側のときはG=-1となり，位相は反転する．
B側のときはG=+1となり，位相は反転しない．

●1接点のスイッチでも作ることができる
　図1は，2接点のスイッチを使った回路でしたが，図5のようにスイッチの位置を変えて1接点のスイッチでも同じ回路動作を作ることができます．

図5　1接点のスイッチを使った回路
スイッチの開/閉で位相を非反転/反転にする．

　図6は，図5のスイッチが閉じているときと開いているときの状態について分けて示しました．図6(a)はスイッチを閉じた状態で，ゲインが「G=-1」の反転アンプになります．図6(b)は先程の図3(b)と同じであり，ゲインが「G=+1」の非反転アンプになります．このようにスイッチの位置を変えて1接点のスイッチの開/閉で位相か非反転/反転になり，振幅は入力信号と同じになる回路を作ることができます．

図6　スイッチの開閉の2つの状態を分けて表した回路

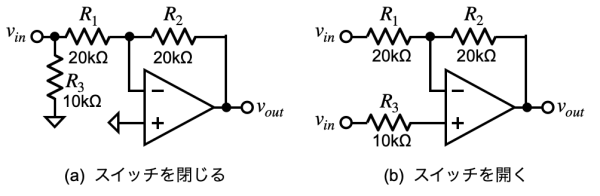
　図7は，図5の回路をシミュレーションした結果をプロットしました．使用したドット・コマンドは，図1と同じです．図7の上段はCtrlの電圧で0s～2ms間は0Vでスイッチは閉じている状態，2ms～4ms間は1Vでスイッチは開いている状態になります．中段は入力信号，下段は出力信号です．0s～2ms間のスイッチが閉じているときは位相が反転して振幅は1Vになることが分かります．同じように2ms～4ms間のスイッチが開いているときは，位相は非反転で振幅は1Vになることが分かります．

図7　図5をシミュレーション結果
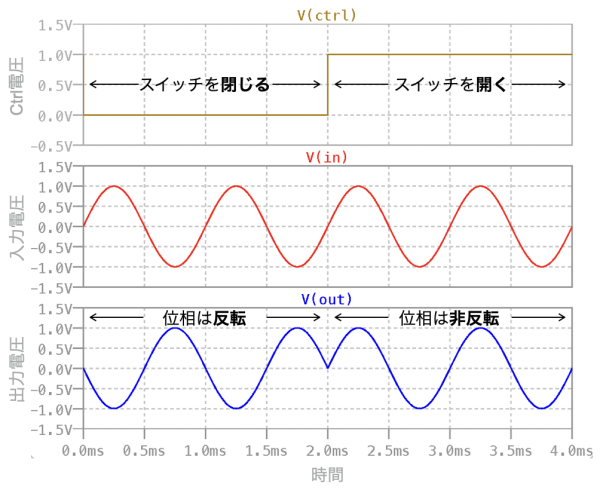
図4の2接点のスイッチの波形と同じになる．

●スイッチの代わりに可変抵抗器を使うと振幅を調整できる
　図8は，スイッチの代わりに可変抵抗器を使った回路です．LTspiceには可変抵抗器はないので，R_3aとR_3bを用い，可変させる量を変数n（0＜n＜1の範囲）で調整するようにしました．

図8　スイッチの代わりに可変抵抗器を用いた回路
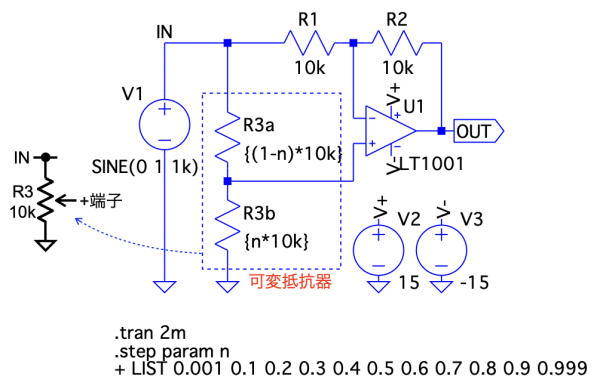
変数nで抵抗の調整をしている．

　図8の可変抵抗器は，入力信号を抵抗分圧してOPアンプの非反転端子に加えています．v_inをR_3aとR_3bで抵抗分圧すると，テブナンの定理よりOPアンプの非反転端子には「nv_in」の電圧と出力抵抗「R_3a||R_3b」を持つ等価電源が加わることになります．この状態をわかりやすく示したものが図9の等価回路になります．ここでは，図9を用いて，nによって出力の位相が反転/非反転のどちらになるかと，そのときの振幅について検討します．

図9　図8の等価回路
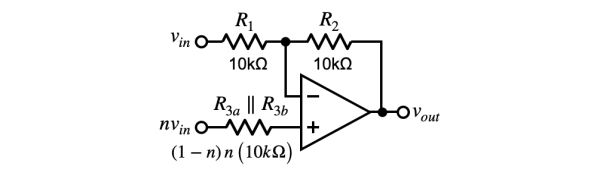
抵抗分圧でnv_inが非反転端子に加わる．

　図9を重ね合わせの理を使って解析します．R₁の左側のv_inを回路に残し，R_3a||R_3bの左側をGNDにしたときの出力電圧をv_out1とすると，反転アンプになります．R₁とR₂の抵抗値は等しいので，入力電圧と出力電圧の関係は式7になります．

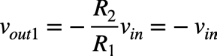・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　同じようにR_3a||R_3bの左側のnv_inを回路に残し，R₁の左側をGNDにしたときの出力電圧をv_out2とすると，非反転アンプになります．R₁とR₂の抵抗値は等しいので,入力電圧と出力電圧の関係は式8になります．

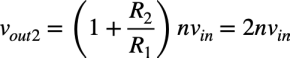・・・・・・・・・・・・・・・・・・・・・・・(8)

　重ね合わせの理より，式7と式8を加え合わせると，入力電圧と出力電圧の関係は式9になります．

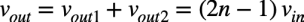・・・・・・・・・・・・・・・・・・・・・・(9)

　式9のゲインは式10になります．

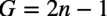・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　式10より，「n=0.5」のときはゲインがゼロとなり，出力信号はゼロになります．「0＜n＜0.5」のときはゲインの符号がマイナスになり位相は反転し，「0.5＜n＜1」のときはゲインの符号がプラスになり位相は非反転になります．このときのゲインは，nによって変わるので，出力信号の振幅はnで調整できることが分かります．

●可変抵抗器を使ったときのシミュレーション
　図8をシミュレーションして出力信号の位相と振幅を確認します．ドット・コマンドの「.tran 2m」は0s～2ms間のトランジェント解析の指定です．「.step」は変数nの値をLISTで指定した数値に順次入れ替えます．
　図10は，図8のシミュレーション結果で上段が入力信号，下段はnが0.001から0.5までのプロットです．「n=0.5」では出力振幅はゼロになり，「0＜n＜0.5」では位相が反転し，nに応じて振幅が変化することが分かります．

図10　図8のn=0.001～0.5をプロット
位相は反転し，可変抵抗器で振幅調整ができる．

　図11は，上段が入力信号，下段は，nが0.5から0.999までのプロットです．図10と同じように「n=0.5」では出力振幅はゼロになり，「0.5＜n＜1」では位相が非反転で，nに応じて振幅が変化することが分かります．

図11　図8のn=0.5～0.999をプロット
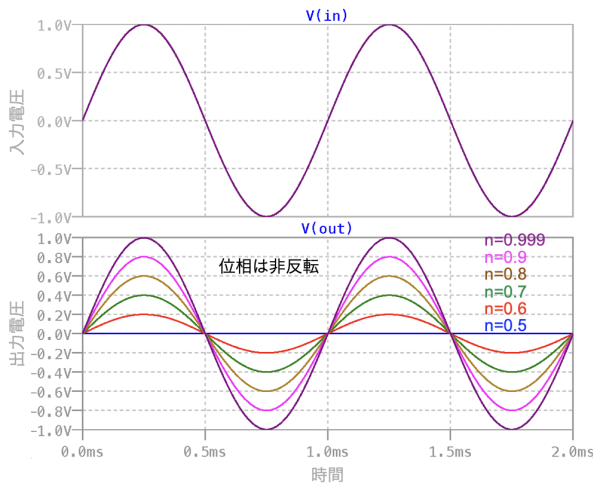
位相は，反転せず，可変抵抗器で振幅調整ができる．

　以上，解説したように，スイッチや可変抵抗器を用いて出力信号の位相を反転/非反転にする回路を作ることができます．このような回路のアプリケーションの一例は,出力信号の位相が反転/非反転になる回路の出力と，元の信号を外部で加算することにより，非反転のときは信号を強調したり，反転のときは信号を抑制したりするときに使われます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_028.zip

●データ・ファイル内容
Plus Minus 1 times Amplifier1.asc：図1の回路
Plus Minus 1 times Amplifier1.plt：図4のプロットを指定するファイル
Plus Minus 1 times Amplifier2.asc：図5の回路
Plus Minus 1 times Amplifier2.plt：図7のプロットを指定するファイル
Plus Minus 1 times Amplifier3.asc：図8の回路
Plus Minus 1 times Amplifier3.plt：図10と図11のプロットを指定するファイル
SPDT.asc，SPDT.asy：2接点のスイッチの回路とシンボル
SPST.asc，SPST.asy：1接点のスイッチの回路とシンボル