信号の減衰を防ぐ入力抵抗

■問題
使用するコマンド ― .OP/.AC/.NET

平賀　公久　Kimihisa Hiraga

　図1は，差動アンプとAMP2の2つの増幅回路にR₁とR₂で負帰還をかけた非反転アンプです．差動アンプには，IN+とIN-間の差動入力抵抗(R_D)とIN+とGND間の同相入力抵抗(R_C)があります．図1の入力(v_in)の右側の直流の入力抵抗(R_IN)は，R_DとR_Cに関係します．その関係として正しいのは(a)～(d)のどれでしょうか．ここでAβは，図1のループ・ゲインです．

図1　差動アンプとAMP2で構成した非反転アンプ
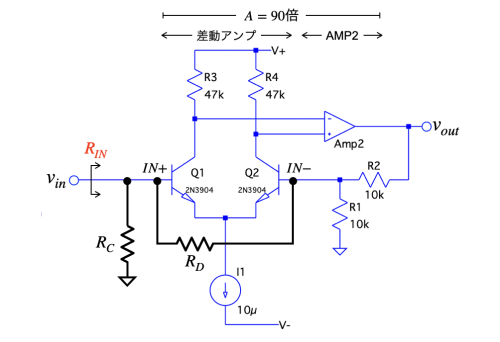
通常，差動入力抵抗(R_D)と同相入力抵抗(R_C)は，Q₁とQ₂の中にあります．さらに，R_Cは基板抵抗にも含まれています．今回は，分かりやすいように回路上に書き出しています．

(a) R_DをAβ倍した入力抵抗に見える
(b) R_DをAβで割った入力抵抗に見える
(c) R_CをAβ倍した入力抵抗に見える
(d) R_CをAβで割った入力抵抗に見える

■ヒント

　入力抵抗(R_IN)を高くするのは，信号源抵抗(R_S)が高いときでも信号が減衰せずにアンプの入力に加えたいからです．
　入力抵抗は，R_DとR_Cで表した式となり，R_DとR_Cのどちらかの抵抗は負帰還の効果でループ・ゲインAβに関係しています．負帰還がかかったときのR_DとR_Cの両端の電圧がどのように見えるかを検討すると分かります．

■解答

(a) R_DをAβ倍した入力抵抗に見える

　v_inから右側の直流の入力抵抗(R_IN)は，R_DとR_Cが関係します．R_DとR_Cが，負帰還の効果でどのように見えるか検討します．図1の負帰還は，一巡のループを形成しており，具体的にはIN+とIN-の電圧差を直流オープン・ループ・ゲイン(A)で増幅した電圧がv_outになります．v_outをR₁とR₂の分圧回路による帰還率(β)で減衰させてIN-へ戻るループになります．
　この負帰還の効果で，IN-の電圧はIN+の電圧とほぼ等しくなるように動き，バーチャル・ショートになります．バーチャル・ショートに関係するのは，抵抗の両端の電圧がIN+とIN-間の電圧になるR_Dになります．R_Cはv_inとGND間にあるので，バーチャル・ショートの影響を受けずにv_inから見るとそのままの抵抗が見えます．なので，R_Cは負帰還の影響を受けないので，(c)と(d)は消えます．
　次に，ここでIN+の電圧をv_in，IN-の電圧をv_IN-，そしてR_Dの両端の電圧差をv_idとします．図1の回路で，v_IN-の電圧は負帰還の効果により式1になります．ここでAβはループ・ゲインです．式1よりAβが1より十分大きいと，v_IN-=v_inと近似できるのでバーチャル・ショートになるのが分かります．

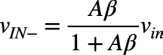・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　R_Dの両端の電圧(v_id)は，v_inとv_IN-の電圧差ですので式2になります．

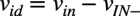・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式1を式2へ代入しv_idを求めます．ここで，Aβは1より十分大きいので「1+Aβ=Aβ」の近似をすると式3になります．

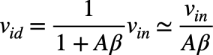・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3より，v_inが変化したとき，R_Dの両端の電圧にかかるv_idは，v_inをAβで除算した低い電圧になります．これがバーチャル・ショートのときのR_Dの両端にかかるわずかな電圧差になります．この関係より，v_inが変化してもR_Dの電圧変化が低くなって，電流は流れにくくなるので，v_inから見たR_DはAβ倍した高い抵抗に見えます．以上より，正解は(a)になります．
　差動入力抵抗(R_D)の物理的な意味は，差動アンプをオープンにしたときのIN+とIN-間の抵抗です．同相入力抵抗はIN+からGND間の抵抗のことで，差動アンプのテール電流の出力抵抗に関係するものや，基板のIN+の配線からGND配線までの絶縁抵抗も含みます．一般に同相入力抵抗(R_C)は差動入力抵抗(R_D)とより高い抵抗値になります．

■解説

●非反転アンプは反転アンプより入力抵抗が高くなる
　負帰還アンプは，入力信号v_inの位置により，図2(a)の非反転アンプと図2(b)の反転アンプになります．非反転アンプと反転アンプの違いは，出力の位相が180°違います．また，R₁とR₂の抵抗値が同じとき，ゲインが違います．さらに，入力抵抗(R_IN)が違います．

図2　非反転アンプと反転アンプの違い
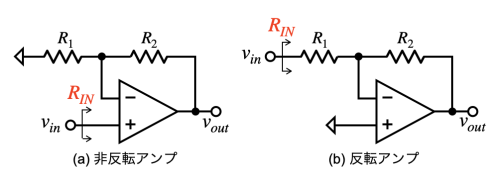
(a) 非反転アンプの入力抵抗は高い　(b) 反転アンプの入力抵抗は低い

　先程検討したように，非反転アンプは，差動入力抵抗(R_D)をAβ倍した抵抗に見えます．一方，反転アンプの反転端子はバーチャル・グラウンドになるので入力抵抗はR₁に見えます．このように，入力抵抗に差があるので，信号源抵抗が高いとき，非反転アンプを用います．
　非反転アンプの入力抵抗は，R_DをAβ倍した高い抵抗になるので，実際の設計では，入力抵抗の計算を省いて進めることが多いと思います．
　以降では具体的にどのくらいの入力抵抗になるのかを，図1の入力抵抗の机上計算をして，その後シミュレーションで確認します．

●差動入力抵抗(R_D)を求める
　図1の入力抵抗(R_IN)を求めるとき，差動入力抵抗(R_D)が必要になるので，ここでは差動アンプのR_Dを机上計算します．図3(a)は，図1の差動アンプを抜き出した回路です．図3(b)は，差動アンプを解析するため，差動アンプのQ₁とR₃の半回路を低周波π型等価回路で表した等価回路です．図3(a)の差動アンプは，左右対称なので，図3(b)の半回路を使って解析することができます．

図3　差動アンプの差動入力抵抗(R_D)を求める回路
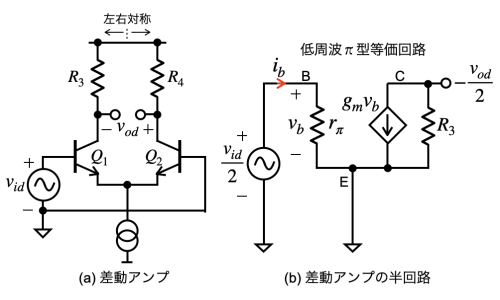
(a) 図1の差動アンプ　(b) Q₁とR₃の半回路をπ型等価回路で表した．

　図3(a)の差動入力抵抗(R_D)は，v_idの電圧変化によるベース電流(i_b)の変化なので，図3(b)を使って「R_D=v_id/i_b」を導きます．まず，図3(b)のベース側でみたキルヒホッフの電圧則は，式4となります．

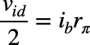・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　ここで，r_πは，式5のトランジスタの直流電流増幅率(β_F)をトランスコンダクタンス(g_m)で除算することにより求めることができます．Q₁の具体的な値を調べると「β_F=307」，g_mはコレクタ電流を「I_C=5μA」，熱電圧を「V_T=26mV」とすると「g_m=I_C/V_T=192μA/V」となり，これらを代入するとr_πは1.6MΩとなります．
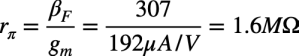・・・・・・・・・・・・・・・・・・・・・・(5)

　次に，式4をv_id/i_bで解いてR_Dを求めると式6になり，式5のr_πを入れると差動入力抵抗(R_D)は3.2MΩになります．

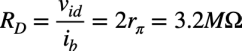・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

●入力抵抗を求める
　図4の非反転アンプのブロック図を用いてv_inから見た入力抵抗を机上計算します．図4は，図1の差動アンプとAMP2の2つの増幅回路を1つにまとめて三角形のアンプの記号にしました．また，図1と同じように差動入力抵抗(R_D)と同相入力抵抗(R_C)を分かりやすいように回路へ図示しました．同相入力抵抗は，反転端子側にもありますが，R₁と並列抵抗になり，通常R₁＜＜R_Cなので無視しています．アンプは非反転端子と反転端子間の電圧差v_idをオープン・ループ・ゲインAで増幅するで，アンプの記号内にある信号源「Av_id」で表しています．入力抵抗を調べるときはオームの法則より「R_IN=v_in/i_in」から求めます．i_inは図4中のi₁からi₄で表すことができるので，各電流を求めていきます．

図4　非反転アンプの入力抵抗(R_IN)を検討するブロック図

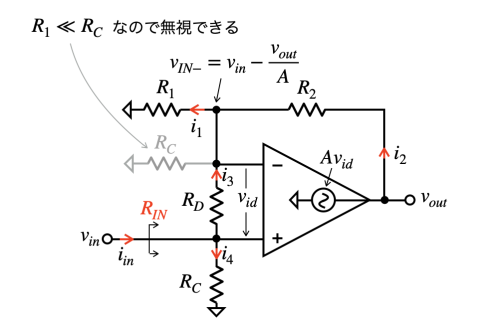
　まず，i₁からi₄の電流を調べるため，図4のノード電圧を求めます．非反転端子と反転端子間の電圧差v_idは，出力電圧(v_out)とオープン・ループ・ゲインAを使って表すと式7になります．

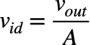・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　反転端子の電圧v_IN-は，v_inからv_idを減じた電圧なので，式7のv_idを使うと式8になります．この電圧は図4中にも示しました．

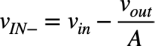・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　次にi₁，i₂，i₃の各電流を求めます．i₁は反転端子の電圧とR₁を使ってオームの法則より式9になります．

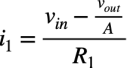・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　i₂はR₂の両端の電圧とR₂を使ってオームの法則より式10になります．

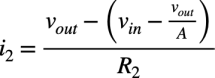・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　i₃は式7のv_idと差動入力抵抗(R_D)使ってオームの法則より式11になります．

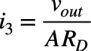・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　反転端子のキルヒホッフの電流則より「i₃=i₁-i₂」なので式12になります．

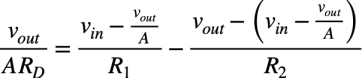・・・・・・・・・・・・・・・・・(12)

　式12を整理すると式13になります．

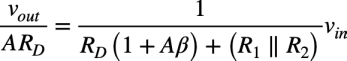・・・・・・・・・・・・・・・・・・(13)

　i₄は，非反転端子の電圧とR_Cを使ってオームの法則より式14になります．

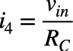・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)

　非反転端子のキルヒホッフの電流則より入力電流i_inは「i_in=i₃+i₄」なので式11と式14を使うと式15になります．

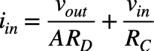・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)

　式15へ式13を代入して i_in/v_inで解くと式16になります．

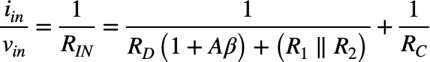・・・・・・・・・・・・・(16)

　式16は「R_D(1+Aβ)+(R₁||R₂)」と「R_C」の並列抵抗を表す式なので，入力抵抗(R_IN)は式17になります．

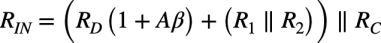・・・・・・・・・・・・・・・・(17)

　式17のAβは，1より十分大きいので「1+Aβ=Aβ」と近似し，「R_D(1+Aβ)＞＞(R₁||R₂)」の関係より(R₁||R₂)を無視すると，入力抵抗(R_IN)は式18になります．

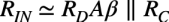・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(18)

　式18より，入力抵抗はR_DAβとR_Cの並列抵抗になります．一般に同相入力抵抗のR_Cは差動入力抵抗のR_Dより十分高い抵抗になるので，入力抵抗(R_IN)は差動入力抵抗(R_D)とループゲインAβの積で決まります．
　図1の具体的な入力抵抗(R_IN)を求めると，R_Dは式6より「R_D=3.2MΩ」，オープン・ループ・ゲインは「A=90」，帰還率は「β=R₁/(R₁+R₂)=0.5」より式19となり，入力抵抗(R_IN)は144MΩになります．このように図1の入力抵抗(R_IN)は144MΩの高い抵抗になります．

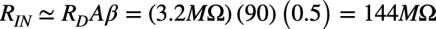・・・・・・・・・・・・(19)

●シミュレーションと机上計算の比較
　図5は，図1の入力抵抗(R_IN)をシミュレーションする回路になります．使用したドット・コマンドは「.OP」，「.AC」，「.NET」です．「.OP」は回路の直流動作点をシミュレーションします．このシミュレーションはトランジスタの直流動作点を調べるのに便利です．「.AC dec 30 0.1 1k」は，0.1Hzから1kHz間を周波数が10倍あたり30ステップの周波数掃引で小信号AC解析を実行するという意味になります．「.NET V1」は小信号AC解析において回路網パラメータを計算する指令で，V1を接続した1ポート回路の入力インピーダンスを求めるという意味になります．

図5　図1のR_INをシミュレーションで調べる回路

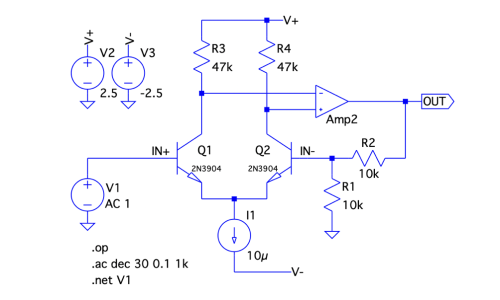
　図6は「.OP」のシミュレーション結果でログ・ファイルに記録されます．ログ・ファイルは，メニュー・バーからView→SPICE Error Logで表示する方法と，ショート・カット・キーの「Crtl+L」を用いる方法があります．図6よりコレクタ電流(I_C)，直流電流増幅率(β_F)，トランスコンダクタンス(g_m)，トランジスタのr_πは，式4と式5で使った数値，および計算結果と同じになるのが分かります．

図6　図5の直流動作点の結果
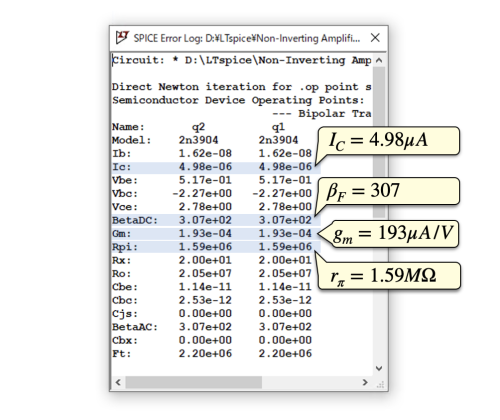
トランジスタの動作点が数値で表示される．

　図7は，図5のオープン・ループ・ゲインと入力抵抗の周波数特性をプロットしました．低周波数の0.1Hzは直流に近いことから，直流付近のオープン・ループ・ゲインは「A=90倍」，入力抵抗は「R_IN=144MΩ」になります．入力抵抗は机上計算した式19と一致することが分かります．

図7　図5の入力抵抗とオープン・ループ・ゲインをプロットした結果

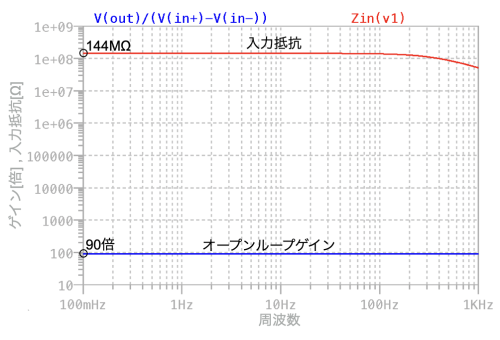
　以上，解説したように直流の入力抵抗は，差動入力抵抗(R_D)にループ・ゲイン(Aβ)を乗じた抵抗に見えます．入力抵抗を高くするのは，信号源抵抗が高いときでも信号が減衰せずにアンプの入力に加えたいからです．
　しかし，実際のアンプのオープン・ループ・ゲイン(A)は，周波数が高くなると小さくなります．そして，帰還率(β)は，R₁とR₂の抵抗比で決まる信号ゲインを高くすると逆に小さくなります．このようなとき，ループ・ゲイン(Aβ)は小さくなりますので，扱う信号周波数帯での信号源抵抗と入力抵抗で信号が減衰しないかの確認が必要だと思います.

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_024.zip

●データ・ファイル内容
Non-Inverting Amplifier input resistance.asc：図5の回路
Non-Inverting Amplifier input resistance.plt：図7のプロットを指定するファイル
AMP.asc：AMP2の回路
AMP.asy：AMP2のシンボル