ブートストラップがあるエミッタ・フォロワの特性

■問題
使用するコマンド ― .OP/.AC/.NET

平賀　公久　Kimihisa Hiraga

　図1は，ブートストラップ(Bootstrap)があるエミッタ・フォロワです．ブートストラップは出力から入力への正帰還のことで，図1では，OUTからC₂とR₄を通り，Q₁ベースの入力までの経路です．これは，C₂による正帰還になります．図1で，ブートストラップの効果として正しいのは(a)～(d)のどれでしょうか．
　ただし，V₁の信号周波数帯において，C₁とC₂のインピーダンスはR₁，R₂，R₄より十分低いとします．また，検討を簡単にするため，ベースからトランジスタ側を見たR_Z1の抵抗値は無限大とします．

図1　ブートストラップがあるエミッタ・フォロワ
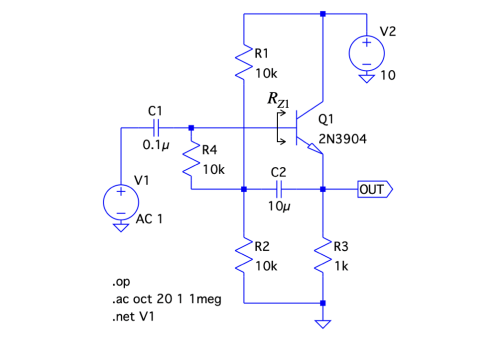
検討を簡単にするためR_Z1は無限大．
ブートストラップの効果として正しいのはどれ?

(a)入力インピーダンスが高くなる
(b)入力インピーダンスが低くなる
(c)ゲインが高くなる
(d)ゲインが低くなる

■ヒント

　C₁とC₂のインピーダンスがR₁，R₂，R₄より十分低いとき，コンデンサはショートと見なせます．ブートストラップの効果を検討するため，C₁をショートした状態で，C₂のショートが無いときと有るときの違いを考えると分かります．ブートストラップという名は，R₄をブーツに例え，ブーツを持ち上げるためにQ₁ベース側が上がる（電圧が高くなる）と，ストラップとなるもう一端のC₂側を自分自身で引き上げる（C₂の正帰還で電圧が高くなる）という動作からきています．

■解答

(a)入力インピーダンスが高くなる

　図1を機能ごとに分けると，Q₁とR₃がエミッタ・フォロワの本体回路，R₁，R₂，R₄はQ₁の直流動作点を決めるバイアス回路，C₁はV₁の交流信号を通過させるカップリング・コンデンサ，C₂はOUTからR₄を通ってベースへ交流信号を正帰還する経路になります．ここでは図1を書き換えて，図2(a)のC₁をショートと見なし，C₂が無いときの等価回路と，図2(b)のC₁とC₂をショートと見なした等価回路を用いて特性の違いを検討します．

図2　小信号等価回路でブートストラップの有無の状態を検討する
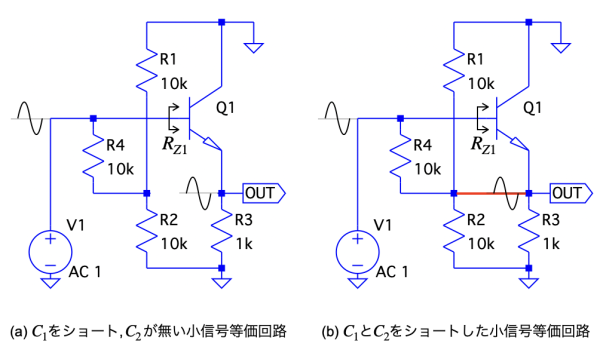
(a)と(b)の違いは，赤色で示した配線の有無

　まず，ゲインについて考えます．図2(a)のQ₁とR₃からなるエミッタ・フォロワの本体回路は，Q₁のベースに加わる交流信号を，ゲインがほぼ1倍でエミッタに伝えます．同様に，図2(b)のエミッタ・フォロワの本体回路もQ₁のベースにV₁の交流電圧が加わるので，エミッタまでのゲインはほぼ1倍になります．図2(a)，(b)共にエミッタは，OUTに繋がるので，2つの回路のゲインの変化はありません．この検討より(c)と(d)は消えます．
　次に，V₁から回路側を見た入力インピーダンスについて検討します．図2(a)，(b)共，Q₁のベースからトランジスタ側を見たR_Z1は，無限大としました．これより，図2(a)のV₁から回路側を見た入力インピーダンスはR₁，R₂，R₄のバイアス回路で決まり「R₄+(R₁||R₂)」になります．一方，図2(b)の入力インピーダンスは，R₄の見かけ上の抵抗値で決まります．具体的に，エミッタ・フォロワのV₁の交流信号とOUTの交流信号は，ほぼ同じなので，R₄の両端の交流電圧もほぼ同じになります．この動作より，R₄の交流電流は極端に低い電流となり，R₄の見かけ上の抵抗値が図2(a)に比べて遥かに高くなります．以上より，正解は(a)の入力インピーダンスが高くなるになります．

■解説

●エミッタ・フォロワの入力インピーダンスに注意する
　図3の回路は，図1のブートストラップの経路となるR₄とC₂を削除し，R₁とR₂の分圧回路に変更した，よく使われるエミッタ・フォロワです．エミッタ・フォロワに求められる交流特性は，ゲインが1倍で，前段の信号を入力では高いインピーダンスで受け，出力では低いインピーダンスになることです．
　以降では，入力インピーダンスに注目し，図3より図1のほうが高い入力インピーダンスになることを解説します．R_Z1は無限大とせず，ベースから見える抵抗を用います．

図3　R₁とR₂のバイアス回路を使ったエミッタ・フォロワ
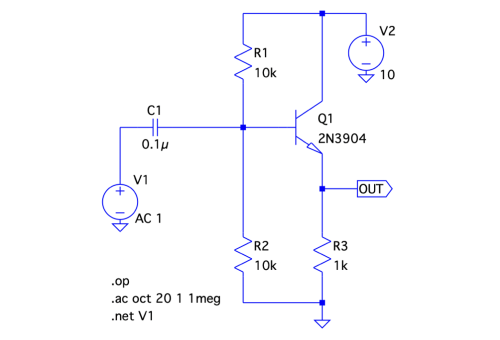
図1の入力インピーダンスと比較する．

●入力インピーダンスの導出
　図3のC₁はR₁とR₂より十分低いインピーダンスになるように設定すると，ショートと見なせるので，図4(a)の回路になります．図4(a)のトランジスタを低周波π型等価回路に置き換えると図4(b)になります．ここでは，図4(b)を使ってベースからトランジスタ側を見たR_Z1の抵抗値を求め，その後，Zinの入力インピーダンスを求めます．

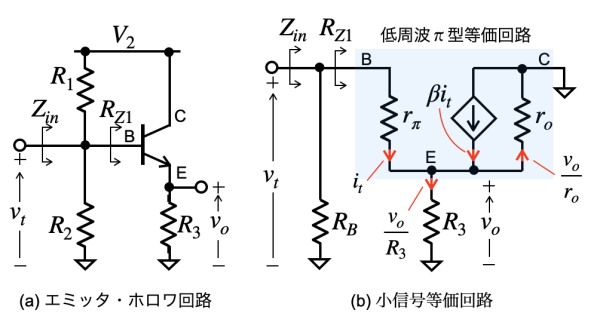
図4　図3のC₁をショートし，トランジスタを低周波π型等価回路に置き換えた回路

　まず，R_Z1をベースの電圧v_tと流れる電流i_tより求めます．v_tはキルヒホッフの電圧則より式1になります．

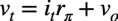・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　また，i_tはトランジスタのエミッタで見ると，キルヒホッフの電流則より式2の関係になります．

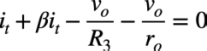・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式2をv_oについて解くと式3になります．

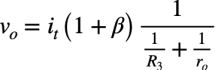・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3を式1へ代入し，ベースからトランジスタ側を見たR_Z1を求めると式4になります．

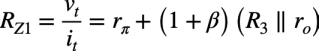・・・・・・・・・・・・・・・・・・・・・(4)

　次に，図4(b)のR_Bは図4(a)のR₁とR₂の並列抵抗を表し，式5になります．

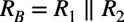・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　図4(b)の入力インピーダンスZinはR_BとR_Z1の並列抵抗なので，式6になります．

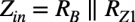・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　具体的な入力インピーダンスを求めるとき，式4中のベース・エミッタ間の抵抗rπ，電流増幅率β，コレクタ・エミッタ間の抵抗(r_o)が必要になります．これらは，LTspiceの「.op」のシミュレーションより分かります．
　図5は，図3の「.op」のシミュレーション結果です．「.op」は回路の直流動作点の解析で，ログ・ファイルに記録されます．ログ・ファイルは，メニュー・バーからView → SPICE Error Logで表示する方法と，ショート・カット・キーの「Crtl+L」を用いる方法があります．

図5　図3の「.op」解析の結果
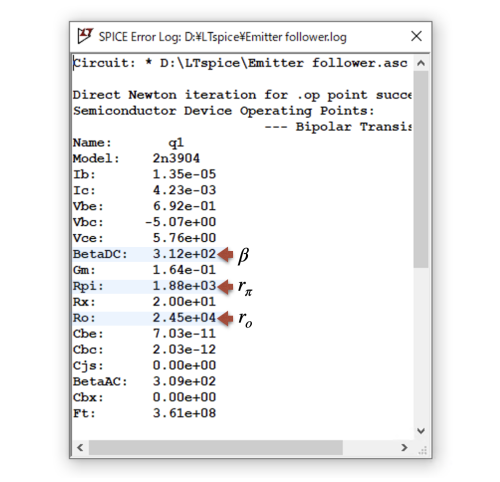
ベース・エミッタ間の抵抗rπ，直流電流増幅率β，コレクタ・エミッタ間抵抗r(_o)が分かる．

　図5の直流動作点の一覧より，直流電流増幅率は「β=312」，ベース・エミッタ間の抵抗は「rπ=1.88kΩ」，コレクタ・エミッタ間の抵抗は「r_o=24.5kΩ」になります．式4へこれらの値と図3の「R₃=1kΩ」を入れると，ベースからトランジスタ側を見た抵抗は「R_Z1=303kΩ」になります．また，式5へ図3の「R₁=R₂=10kΩ」を入れると「R_B=5kΩ」になります．最後に式6へR_Z1とR_Bを入れると，「Zin=4.9kΩ」になります．
　このように，エミッタ・フォロワ本体のR_Z1は，高い抵抗値になりますが，バイアス回路のR_Bの抵抗値が低くなるので，入力インピーダンスのZinは4.9kΩの低い抵抗値になります．

●入力インピーダンスとゲインのシミュレーション
　図6は，図3のシミュレーション結果です．上段が入力インピーダンスの周波数特性で，下段がゲインの周波数特性です．使用したドット・コマンドは「.AC」と「.NET」です．図3の「.ac oct 20 1 1meg」は，1Hzから1MHz間を周波数が2倍あたり20ステップの周波数掃引で小信号AC解析を実行するという意味になります．「.net V₁」は，小信号AC解析において回路網パラメータを計算する指令で，V₁を接続した1ポート回路の入力インピーダンスを求めるという意味になります．「.NET」は「.AC」の周波数掃引と一緒に使います．
　図6の1kHzを境にすると，低周波側はC₁により交流信号が通過しない周波数帯となり，高周波側はゲインが1倍のバッファとして使える信号周波数帯になります．図6の上段より，10kHzの入力インピーダンスを調べると「Zin=4.9kΩ」であり，先程の式6の机上計算と同じになります．図6の下段より，同じ周波数でゲインを調べると「G=0.993」であり，ほぼ1倍になるのが分かります．

図6　図2のシミュレーション結果
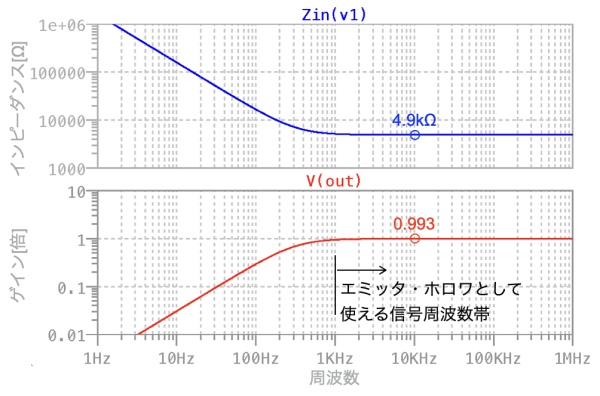
上段はV₁から見た入力インピーダンスの周波数特性．
下段はゲインの周波数特性．

●ブートストラップによる入力インピーダンスの変化
　次にブートストラップがあるエミッタ・フォロワの入力インピーダンスZinを求めます．図1のC₁とC₂はR₁，R₂，R₄より十分低いインピーダンスになるように設定すると，ショートと見なせるので図7(a)の回路になります．図7(a)のトランジスタを低周波π型等価回路に置き換えると図7(b)になります．R_BはR₁とR₂の並列抵抗です．

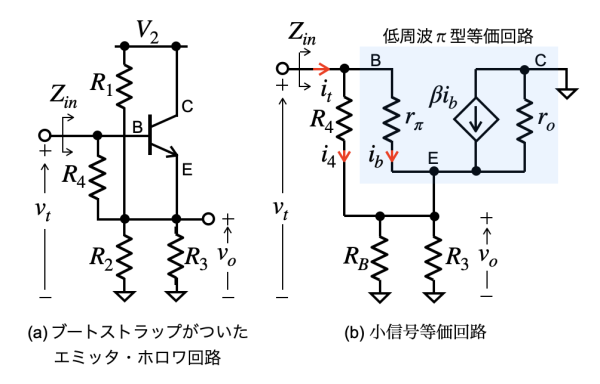
図7　図1のC₁とC₂をショートし，トランジスタを低周波π型等価回路に置き換えた回路

　図7(b)のZinをベースの電圧v_tと流れる電流i_tより求めます．i_tはトランジスタのベースで見ると，キルヒホッフの電流則より式7になります．

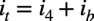・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　i₄はR₄の両端の電圧と抵抗値を使い，オームの法則より式8になります．

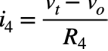・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　同じようにibは，rπ両端の電圧と抵抗値を使い，オームの法則より式9になります．

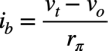・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　エミッタ・フォロワのゲインは式10になります．

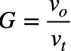・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　式7へ式8と式9を入れてi_t/v_tになるように式を整理し，式10のゲインを用いると式11になります．

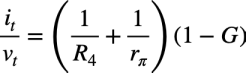・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　入力インピーダンスは，式11の逆数なので式12となります．

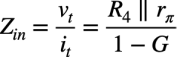・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)

　ゲインが1のとき入力インピーダンスは無限大になります．しかし，実際のゲインは，1より僅かに小さな値なので，有限の高い入力インピーダンスになります．
　式12中のベース・エミッタ間の抵抗rπはLTspiceの「.op」のシミュレーションより分かります．
　図8は，図1の「.op」のシミュレーション結果で，「rπ=1.94kΩ」になります．またゲインは後に示す図9の周波数特性より「G=0.9921」になります．図1の「R₄=10kΩ」の抵抗を使うと，式12は「Zin=206kΩ」になります．

図8　図1の「.op」解析の結果
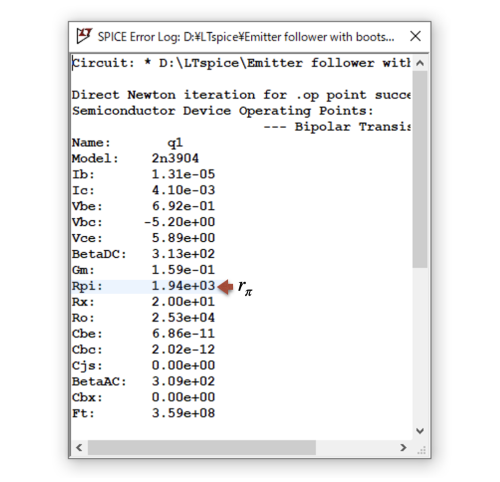
ベース・エミッタ間の抵抗rπが分かる．

●ブートストラップの効果をシミュレーションで確認する
　図9は，図1のシミュレーション結果です．上段が入力インピーダンスの周波数特性で，下段がゲインの周波数特性です．使用したドット・コマンドは図3と同じ「.AC」と「.NET」になります．
　図9より，交流信号が通過しない周波数帯は100Hzより低周波側になり，図6と比べると信号周波数帯が広がっています．これは，C₁のコンデンサが同じ容量でもZinが高くなるので，低周波の信号が通過するようになります．図9上段より10kHzの入力インピーダンスを調べると「Zin=210.5kΩ」であり，先程の式12の机上計算とほぼ同じです．図9下段より，同じ周波数でゲインを調べると「G=0.9921」であり，ほぼ1倍になるのが分かります．

図9　図1のシミュレーション結果
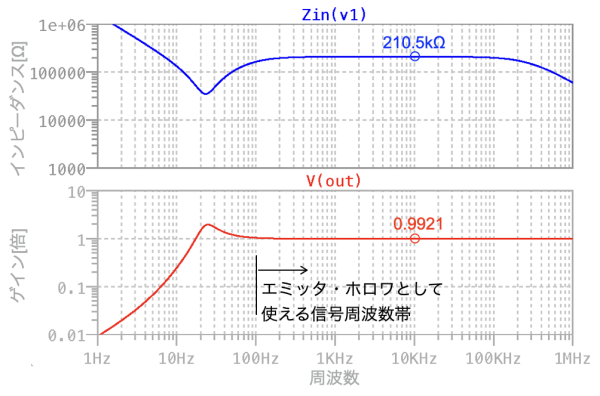
上段はV₁から見た入力インピーダンスの周波数特性．
下段はゲインの周波数特性．

　以上のように，図3のエミッタ・フォロワの直流動作点を決めるバイアス回路は，入力インピーダンスを低くします．対策として図1のブートストラップがあるエミッタ・フォロワを用いると入力インピーダンスを高くすることができます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_014.zip

●データ・ファイル内容
Emitter follower with bootstrap.asc：図1の回路
Emitter follower with bootstrap.plt：図1のプロットを指定するファイル
Emitter follower.asc：図3の回路
Emitter follower.plt：図3のプロットを指定するファイル