ベース接地アンプのゲインとコーナ周の求め方

■問題
使用するコマンド ― .AC/.OP

平賀　公久　Kimihisa Hiraga

　図1は，V₁が入力信号，OUTが出力になるベース接地アンプです．この回路は，交流の信号だけ増幅し，直流の信号を増幅しません．交流の信号は，低周波側のコーナ周波数(f_CL)から高周波側のコーナ周波数(f_CH)までとなります．図1のベース接地アンプで，f_CLからf_CHの間の交流の信号のゲインは(a)～(d)のどれでしょうか．ただし，Q₁のコレクタ電流は「I_C=1.55mA」とします．

図1　V₁が入力，OUTが出力のベース接地アンプ
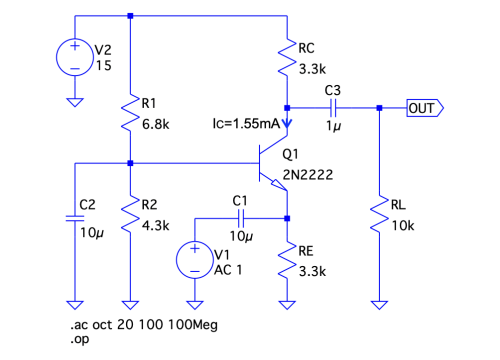
交流の信号のゲインは何倍？

(a)+1倍　(b)-1倍　(c)+150倍　(d)-150倍

■ヒント

　ゲインの符号は，＋が入力と出力の位相が同相となる非反転アンプのゲインで，-が位相が逆相となる反転アンプのゲインを表しています．トランジスタを小信号等価回路に置き換えて検討すると分かります．

■解答

(c)+150倍

●交流ゲインの求め方
　図2は，図1のトランジスタを低周波T型等価回路に置き換えた小信号等価回路です．低周波側のコーナ周波数(f_CL)から高周波側のコーナ周波数(f_CH)の間のゲインを検討するときは，C₁，C₂，C₃のコンデンサのインピーダンスは低くみなせるので，ショートにしています．

図2　図1の通過域における小信号等価回路

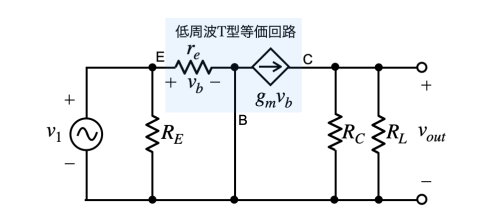
　まず，信号の流れより，ゲインの符号がどうなるかを検討します．図2において，エミッタにつながる入力信号(v₁)の電圧は，低周波T型等価回路内の入力抵抗(r_e)の両端の電圧(v_b)となります．コレクタからはv_bで制御した電流がR_CとR_Lの並列抵抗(R_C||R_L)に流れ，その電圧降下が出力電圧(v_out)になります．v₁の電圧が高くなるとv_bの電圧も高くなり，コレクタから(R_C||R_L)の並列抵抗へ電流が流れてv_outの電圧は高くなります．この動作は入力と出力の位相は同相であることを示しています．なので，図2は非反転アンプであり，ゲインの符号は＋になって(b)と(d)は候補から消えます．
　次にゲインの値を求めます．図2のv_outはv₁とv_bの電圧は同じなので，式1となります．

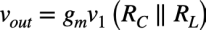・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　式1中のトランスコンダクタンス(g_m)は，コレクタ電流「I_C=1.55mA」と熱電圧「V_T=26mV」より式2となります．

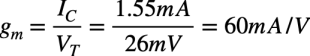・・・・・・・・・・・・・・・・・・・・・(2)

　式1中のR_CとR_Lの並列抵抗は「R_C=3.3kΩ」，「R_L=10kΩ」より，式3となります．

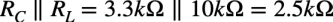・・・・・・・・・・・・・・・・・・・・(3)

　ゲインは，v_outとv₁の比なので，式1をv_out/v₁で解いて，式2と式3の値を入れると式4になります．

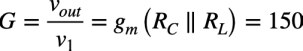・・・・・・・・・・・・・・・・・・・・・・(4)

　以上の検討より，図2のゲインは，(c)+150倍となります．

■解説

●机上計算でコーナ周波数を求める
　解答では信号が通過する周波数帯の交流ゲインを調べました．以降の解説では，信号が通過する周波数と減衰する周波数の境目となる，低域側のコーナ周波数(f_CL)と，高域側のコーナ周波数(f_CH)を机上計算し，周波数応答の全体像を調べます．そして，机上計算と図1のシミュレーションのコーナ周波数を比較します．

●ベース接地アンプの解析で用いる小信号等価回路
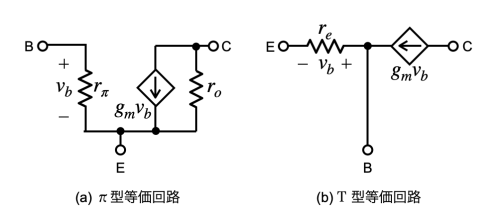
　アンプの解析では，入力側には入力抵抗のみがあり，出力側は入力側の電圧で制御した電流となった方が，信号の流れがストレートになって解析しやすくなります．よく用いられるトランジスタの小信号等価回路は，図3(a)のπ型等価回路です．しかし，π型等価回路をベース接地アンプに用いると，入力となるエミッタに抵抗以外の素子がつくことから扱いにくくなります．そこで，ベース接地アンプで用いる小信号等価回路は，π型等価回路を書き直した図3(b)のT型等価回路を用いて，解析を簡単にします．T型等価回路は，エミッタから見ると入力抵抗となるr_eのみとなり，出力は入力の電圧で制御したコレクタ電流となります．図2を使ったゲインの計算も，T型等価回路を使っているので，計算が簡単になっています．回路の解析は，扱いやすい等価回路へ変えていくと，検討時間の短縮につながります．

図3　2つの小信号等価回路

●ベース接地アンプについて
　ベース接地アンプは，エミッタが入力，コレクタが出力となる非反転アンプとなります．電圧ゲインは式4であり，g_mの調整(コレクタ電流の調整)と負荷抵抗の調整により，幅広い電圧ゲインの設定ができます．エミッタから見たトランジスタ側の入力抵抗は「r_e=1/g_m」となり，式2のg_mを使うと「r_e=17Ω」ですので，低くなるのが分かります．このため，信号源抵抗が高いと，低い入力抵抗との間で信号電圧が減衰するので，使い辛い一面もあります．一方，電流ゲインで見ると，エミッタ電流とコレクタ電流はほぼ等しいので1となり，低い入力抵抗で信号電流を受けて，高い出力抵抗で電流を出力する，電流バッファとして使われることもあります．他の増幅回路と組み合わせることにより，前段の出力電流をベース接地アンプで受けて，高い出力抵抗で電流信号を次段へ伝えるカスコード回路にも使われています．

●低周波側のコーナ周波数(f_CL)の求め方
　図4は，図1のトランジスタを低周波T型等価回路に置き換えた小信号等価回路です．R_SはV₁の信号源抵抗です．低周波でのコーナ周波数を求める場合，この図を使って低周波でのコーナ周波数を検討します．

図4　図1の低周波帯における小信号等価回路

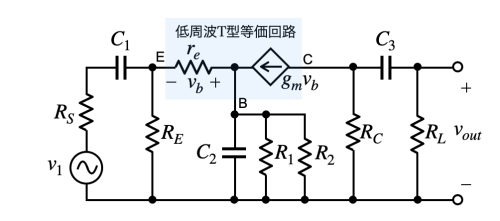
　コーナ周波数は，伝達関数を解いて求めると計算量が多くなります．そこで，C₁，C₂，C₃に関係する低周波のコーナ周波数は，Short-Circuit Time Constant法を使って近似します．Short-Circuit Time Constant法は電圧源(図4ではv₁)をショートにします．そして複数あるコンデンサの1つを残し，他のコンデンサは十分に低いインピーダンスとみなしたショートの条件でコーナ周波数を求めます．これをコンデンサの数だけ繰り返して検討し，最も高い周波数がコーナ周波数となります．

・C₂とC₃をショートした回路
　図5は，図4のC₁を残し，C₂とC₃をショートした小信号等価回路です．

図5　図4のC₂とC₃をショートした小信号等価回路

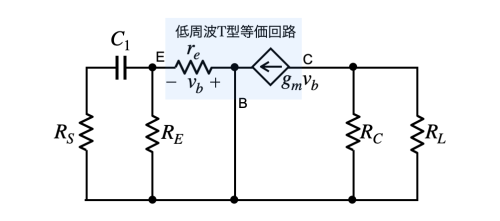
　図5より，C₁に付くテブナン等価抵抗(R_THV1)は式5となります．

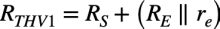・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　C₁による低域側のコーナ周波数をf_CL1とすると，式5のテブナン等価抵抗を使って式6となります．

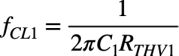・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式6の具体的な周波数を机上計算します．図1では信号源抵抗が無いので「R_S=0Ω」，回路定数より「R_E=3.3kΩ」，コレクタ電流「I_C=1.55mA」と熱電圧「V_T=26mV」より「r_e=1/g_m=V_T/I_C=17Ω」となります．式5へ抵抗値を入れると「R_THV1=17Ω」になり，コンデンサの容量は「C₁=10μF」ですので，式6は「f_CL1=936Hz」となります．

・C₁とC₃をショートした回路
　図6は，図4のC₂を残し，C₁とC₃をショートした小信号等価回路です．ベースからトランジスタ側を見た等価抵抗(R_Z1)の計算を簡単にするため，π型等価回路へ置き換えています．ベースからトランジスタ側を見た等価回路(R_Z1)は，電流増幅率をβとすると，エミッタ側のR_SとR_Eの並列抵抗(R_S||R_E)を(1+β)倍して，r_πを加えた抵抗に見えます．

図6　図4のC₁とC₃をショートした小信号等価回路
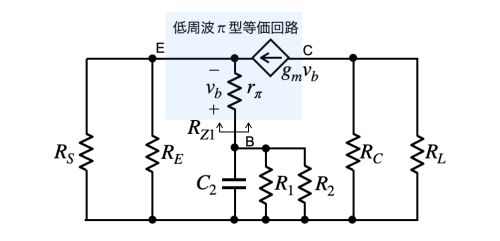
T型等価回路からπ型等価回路へ置き換えた．

　この等価抵抗を用いると，図6のC₂に付くテブナン等価抵抗(R_THV2)は式7となります．

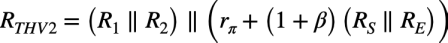　　・・・・・・・・・・(7)

　C₂による低域側のコーナ周波数をf_CL2とすると，式7のテブナン等価抵抗を使って式8となります．

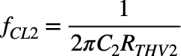・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　式8の具体的な周波数を机上計算します．図1の抵抗は「R_S=0Ω」，「R_E=3.3kΩ」，「R₁=6.8kΩ」，「R₂=4.3kΩ」で，トランジスタの電流増幅率は「β=200」とします．トランジスタのg_mはコレクタ電流「I_C=1.55mA」と熱電圧「V_T=26mV」より「g_m=I_C/V_T=60mA/V」となります．r_πはトランジスタのg_mと電流増幅率のβより，「r_π=β/g_m=3.3kΩ」になります．これらの値を使うと，式7は「R_THV2=1.5kΩ」になります．コンデンサの容量は「C₂=10μF」ですので，式8は「f_CL2=11Hz」となります．

・C₁とC₂をショートした回路
　図7は，図4のC₃を残し，C₁とC₂をショートした小信号等価回路です．

図7　図4のC₁とC₂をショートした小信号等価回路

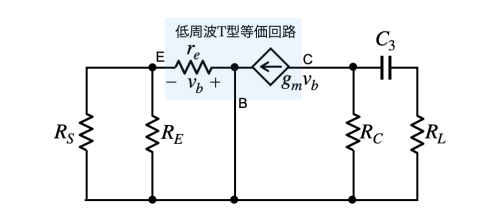
　図7よりC₃に付くテブナン等価抵抗(R_THV3)は式9となります．

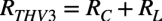・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　C₃による低域側のコーナ周波数をf_CL3とすると，式9のテブナン等価抵抗を使って式10となります．

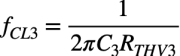・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　式10の具体的な周波数を机上計算します．図1の「R_C=3.3kΩ」，「R_L=10kΩ」より，式9は「R_THV3=13.3kΩ」になります．コンデンサの容量は「C₃=1μF」ですので，式10は「f_CL3=12Hz」となります．
　以上の検討より，低域側のf_CL1，f_CL2，f_CL3の中で最も周波数が高いのは「f_CL1=936Hz」となります．この周波数が，おおよその低域側のコーナ周波数になります．

●高周波側のコーナ周波数(f_CH)の求め方
　図8は，図1のトランジスタを高周波用のT型等価回路に置き換えてC₁，C₂，C₃のコンデンサをショートした小信号等価回路です．高周波でのコーナ周波数を求める場合，次のように行います．
　高周波になるとベースとエミッタ間の接合容量C_π，ベースとコレクタ間の接合容量C_μが無視できないため，2つの接合容量を図3(b)へ加えた等価回路となります．C_πとC_μの具体的な接合容量は，「C_π=63.7pF」，「C_μ=4.3pF」になります．これは後に解説する「.op」の直流動作点解析で調べることができます．

図8　図1の高周波帯における小信号等価回路
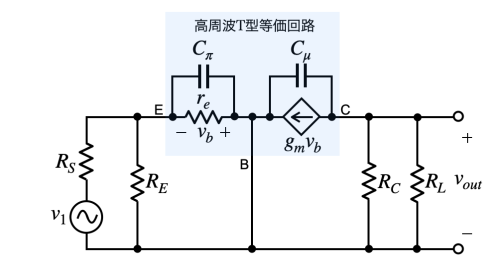
C_πはベースとエミッタ間にある接合容量．
C_μはベースとコレクタ間にある接合容量．

　高周波のコーナ周波数は，Open-Circuit Time Constant法を使って近似します．Open-Circuit Time Constant法は電圧源(図8ではv₁)をショートにします．そして複数あるコンデンサの1つを残し，他のコンデンサはアンプの周波数特性に影響を与えないようにオープンとしたときの時定数を求めます．各々の時定数を合算した後の式に対して逆数をとると，おおよそ全体のコーナ周波数になります．

・C_πをオープンにした回路
　図9は図8のC_μを残し，C_πをオープンにした小信号等価回路です．

図9　図8のC_πをオープンにした小信号等価回路

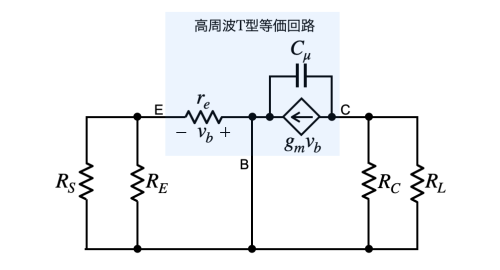
　図9よりC_μに付くテブナン等価抵抗(R_THV4)は式11となります．

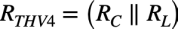・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　式11の具体的なテブナン等価抵抗を机上計算すると，図1の「R_C=3.3kΩ」と「R_L=10kΩ」より「R_THV4=2.5kΩ」となります．

・C_μをオープンにした回路
　図10は図8のC_πを残し，C_μをオープンにした小信号等価回路です．

図10　図8のC_μをオープンにした小信号等価回路

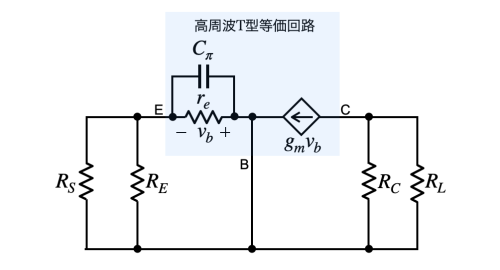
　図10よりC_πに付くテブナン等価抵抗(R_THV5)は式12となります．

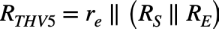・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)

　式12の具体的なテブナン等価抵抗を机上計算すると，図1では信号源抵抗が無いので，「R_S=0Ω」より「R_THV5=0Ω」となります．

　Open-Circuit Time Constant法を使って近似した高周波側のコーナ周波数は式13となります．

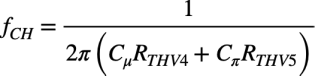・・・・・・・・・・・・・・・・・・・・(13)

　トランジスタのベース・エミッタ間の接合容量は「C_π=63.7pF」，ベース・コレクタ間の接合容量は「C_μ=4.3pF」，テブナン等価抵抗は「R_THV4=2.5kΩ」と「R_THV5=0Ω」より，式13の高域側のコーナ周波数は，おおよそ「f_CH=15MHz」となります．

●トランジスタの接合容量をシミュレーションで調べる
　図111は，図1の「.op」のシミュレーション結果です．

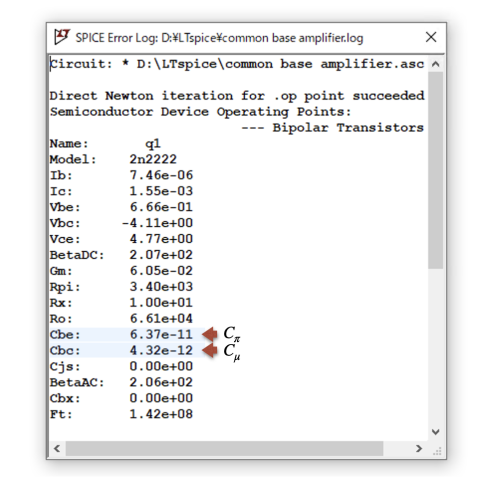
図11　図1の.op解析の結果 CbeはC_π，CbcはC_μ の接合容量．

　「.op」は，回路の直流動作点の解析となります．「.op」の結果はログ・ファイルにあるので，メニュー・バーからView → SPICE Error Logで表示させる方法と，ショート・カット・キーの「Crtl+L」を用いる方法があります．
　図11には，CbeとCbcがあり，回路の直流電圧が加わった条件での，ベース・エミッタ間接合容量(CbeはC_π)，ベース・コレクタ間接合容量(CbcはC_μ)になります．この2つの接合容量は，前述の高周波応答の机上計算で使用しました．

●机上計算とシミュレーションのコーナ周波数を比較
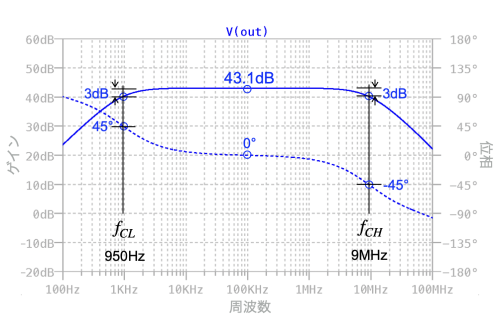
　図1の「.ac oct 20 100 100Meg」は，100Hzから100MHz間を周波数が2倍あたり20ステップの周波数掃引で，小信号AC解析を実行するという意味になります．図12は，図1の「.AC」のシミュレーション結果で，ゲインと位相をプロットしました．
　解答の+150倍はデシベルに直すと43.5dBです．図12の100kHzでのゲインを調べると43.1dBであり一致します．また位相は100kHzで0°であり，入力と出力は同相であることが分かります．次に低域と高域のコーナ周波数の机上計算は「f_CL1=936Hz」，「f_CH=15MHz」です．図12では，f_CL1はほぼ等しく，f_CHも近い周波数に近似できているのが分かります．