エミッタ・フォロワ回路の低域側コーナ周波数

■問題
使用するコマンド ― .AC/.NET

平賀　公久　Kimihisa Hiraga

　図1は，入力側のC₁と出力側のC₂で交流結合し，交流のみ通過させるハイ・パス・フィルタ特性のエミッタ・フォロワ回路です．V₁が入力信号で，OUTが出力です．通過域のゲインは約1倍で，バッファ回路として使われます．この回路の低域側のコーナ周波数は(a)～(d)のどれでしょうか．ただし，Q₁のコレクタ電流は「I_C=4.3mA」，電流増幅率は「β=200」とします．

図1　C₁とC₂で交流結合したエミッタ・フォロワ回路
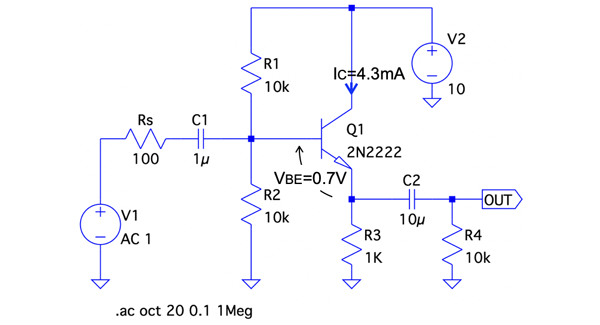
低域側のコーナ周波数は何Hz？

(a)1Hz　(b)2Hz　(c)16Hz　(d)32Hz

■ヒント

　図1のコーナ周波数は，コンデンサと抵抗の積の逆数で決まります．コーナ周波数を検討するときは，C₂をショートしてC₁と回路の抵抗で決まるコーナ周波数と，逆にC₁をショートしてC₂と回路の抵抗で決まるコーナ周波数のどちらか高い方になります．ちなみに，コーナ周波数は信号が通過できるようになる周波数です．また，通過域の高域側のコーナ周波数は，トランジスタの特性で決まります．

■解答

(d)32Hz

　エミッタ・フォロワ回路は，コモン・コレクタ回路とも呼ばれます．図1のC₁とC₂に関係するコーナ周波数はShort-Circuit Time Constant法を使って近似値を算出すると計算量が少なくなります．Short-Circuit Time Constant法は，図1の信号源(V₁)をショートにします．そして複数あるコンデンサの1つを残し，他のコンデンサは十分に低いインピーダンスとみなしたショートの条件でコーナ周波数を求めます．これをコンデンサの数だけ繰り返して検討し，どちらか高い方の周波数がコーナ周波数となります．

●C₁を残してC₂をショートした回路
　まず，図2のようにトランジスタを低周波π型等価回路に置き換えて，C₁を残してC₂をショートした回路でコーナ周波数を検討します．図2のR_Bは図1のR₁とR₂の並列抵抗を表し，R_Z1はベースからトランジスタ側を見た等価抵抗です．

図2　C₂をショートして周波数特性を検討する回路
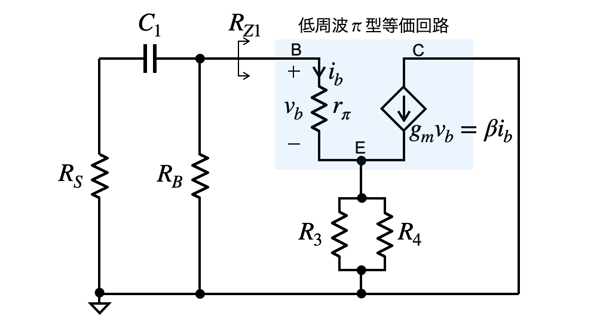
トランジスタは低周波π型等価回路に置き換えている．

　コーナ周波数は，時定数であるCRの積の逆数で，CはC₁の容量，Rはテブナンの定理よりC₁に付くテブナン等価抵抗となります．C₁に付くテブナン等価抵抗（R_THV1）はR_BとR_Z1の並列抵抗を「R_B||R_Z1」とすると，図2より式1となります．

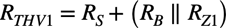・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　式1のR_Bは図1のR₁とR₂の並列抵抗なので式2となります．

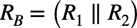・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式1のR_Z1はベースからトランジスタ側を見た等価抵抗です．R_Z1はトランジスタの電流増幅率をβとすると，エミッタ側に付くR₃とR₄の並列抵抗を約（1+β）倍した抵抗に見えるので式3となります．

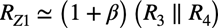・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　C₁による低域側のコーナ周波数をf_C1とすると，式1のテブナン等価抵抗を使って式4となります．

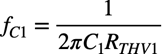・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4の具体的な周波数を机上計算します．式2のR_Bは「R₁=R₂=10kΩ」より「R_B=5kΩ」となります．式3のR_Z1は「R₃=1kΩ」，「R₄=10kΩ」，「β=200」より「R_Z1=183kΩ」となります．式1のテブナン等価抵抗は，「R_S=100Ω」と机上計算したR_B，R_Z1より「R_THV1=4.97kΩ」になります．式4の低域側のコーナ周波数は「C₁=1μF」とR_THV1を使い「f_C1=32Hz」となります．

●C₂を残してC₁をショートした回路
　次に，図3のC₂を残してC₁をショートした回路でコーナ周波数を検討します．図3のR_Z2はエミッタからトランジスタ側を見た等価抵抗です．

図3　C₁をショートして周波数特性を検討する回路
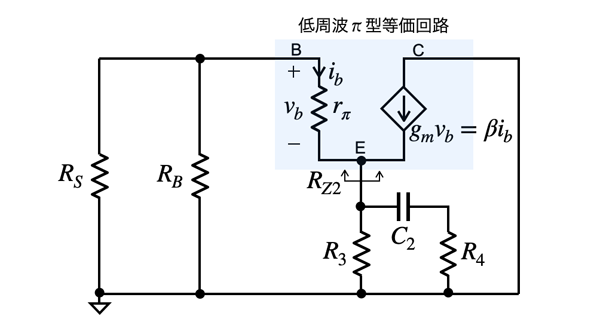
トランジスタは低周波π型等価回路に置き換えている．

　C₂に付くテブナン等価抵抗（R_THV2）はR₃とR_Z2の並列抵抗を「R₃||R_Z2」とすると，図2より式5となります．

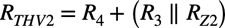・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5のR_Z2は，エミッタからトランジスタ側を見た等価抵抗です．R_Z2はトランジスタの電流増幅率をβとすると，ベース側に見える抵抗を約（1+β）倍小さくした抵抗なので式6となります．

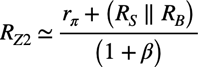・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　C₂による低域側のコーナ周波数をf_C2とすると，式5のテブナン等価抵抗を使って式7となります．

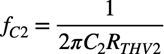・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式7の具体的な周波数を机上計算します．式6のR_Sは「R_S=100Ω」，R_Bは「R_B=5kΩ」，βは「β=200」，r_πはベースとエミッタ間の抵抗で「r_π=β/gm」となります．gmは図1のコレクタ電流「I_C=4.3mA」と熱電圧「V_T=26mV」より「gm=I_C/V_T=165mA/V」となるので，「r_π=1.2kΩ」になります．これより式6のエミッタからトランジスタ側を見た等価抵抗は「R_Z2=6.5Ω」になります．
　式5のテブナン等価抵抗はR₃，R₄，R_Z2より，「R_THV2=10kΩ」になります．式7の低域側のコーナ周波数は「C₂=10μF」とR_THV2を使って「f_C2=1.6Hz」となります．以上で検討したf_C1とf_C2より，周波数が高い方がコーナ周波数になるので，正解は(d)32Hzになります．

■解説

●ベースとエミッタから見た等価抵抗について
　図1の低域側コーナ周波数の検討からも分かるように，回路の周波数応答を求めるときは，ベースやエミッタからトランジスタ側を見たときの等価抵抗を調べなければなりません．よく使うのは「ベースからエミッタ側に付く抵抗を見ると（1+β）倍大きく見える」，「エミッタからベース側に付く抵抗を見ると（1+β）倍小さく見える」の近似値があり，暗記している方も多いと思います．
　等価抵抗の計算は，ここでは割愛します．しかし，考え方として，ベースに加えた交流電圧はゲインが約1倍で，エミッタに伝達されて同じ交流電圧になります．そして，ベース電流とエミッタ電流には「IE=(1+β)IB」の関係があり，同じ交流電圧の変化でベース電流とエミッタ電流は（1+β）倍の差があることになります．
　以降の解説では，LTspiceの「.NET」コマンドを使って，ベースとエミッタからトランジスタ側を見たときの等価抵抗をシミュレーションし，式3と式6の近似値とほぼ一致することを確認します．そして「.AC」コマンドを使って図1の周波数応答をシミュレーションし，低域側のコーナ周波数の机上計算とおおよそ同じになることを確認します．

●ベースからトランジスタ側を見た抵抗の確認
　図4は，図1のC₂がショートの状態で，ベースからトランジスタ側を見た，R_Z1を調べる回路です．図1のベース電圧は，R₁とR₂の抵抗分圧により約5Vとなります．そのため，図4ではV₁から5Vを加えています．

図4　ベースから見た抵抗をシミュレーションする回路

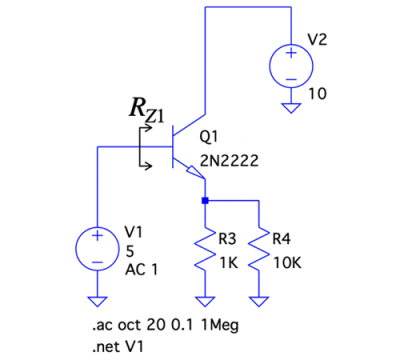
　使用するドット・コマンドは「.AC」と「.NET」です．図4の「.ac oct 20 0.1 1Meg」は，0.1Hzから1MHz間を周波数が2倍あたり20ステップの周波数掃引で小信号AC解析を実行するという意味になります．「.net V1」は，小信号AC解析で回路網パラメータを計算する指令で，V₁を接続した1ポート回路（図4ではベースからトランジスタ側を見た回路）の入力インピーダンスを求めるという意味になります．「.NET」は「.AC」の周波数掃引と一緒に使います．
　図5は，図4のシミュレーション結果です．波形ビューワのメニュー・バーから「Plot settings」→「Add Traces」と進み，入力インピーダンスを表す「Zin(v1)」をプロットした結果です．プロットの縦軸は「Decibel」から「Linear」へ変更しました．このプロットがR_Z1の周波数特性を表しています．

図5　図4のシミュレーション結果低周波の抵抗は180kΩ．

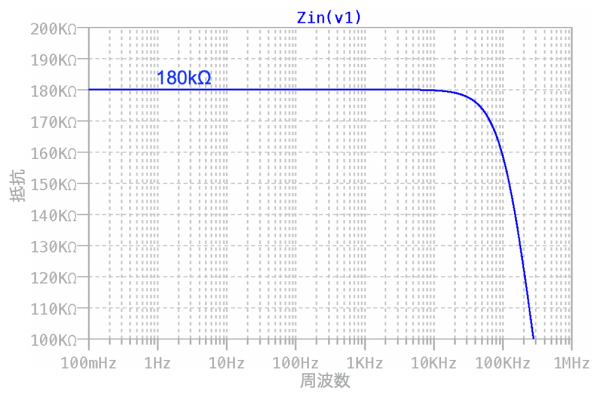
　図5のプロットより，低周波の抵抗は180kΩとなり，式3を使って机上計算した「R_Z1=183kΩ」とほぼ同じです．これより式3によるR_Z1の近似値とシミュレーション結果は，ほぼ等しいことが確認できました．

●エミッタからトランジスタ側を見た抵抗のシミュレーション
　図6は，図1のC₁がショートの状態で，エミッタからトランジスタ側を見たR_Z2を調べる回路です．図1のエミッタ電流は約4.3mAなので，図6では電流源で4.3mAを加えています．エミッタからトランジスタ側を見た抵抗を調べるので，ドット・コマンドは「.net I1」へ変更しました．このドット・コマンドは，I₁を接続した1ポート回路（図6ではエミッタからトランジスタ側を見た回路）の入力インピーダンスを求めるという意味になります．「.ac oct 20 0.1 1Meg」は図4と同じです．

図6　エミッタから見た抵抗をシミュレーションする回路

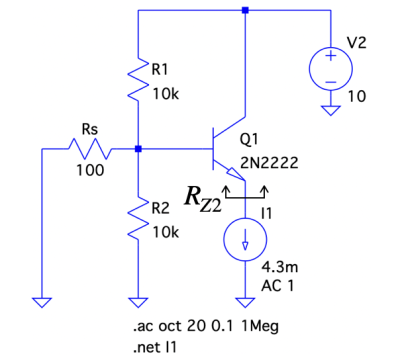
　図7は，図6のシミュレーション結果で，「Zin(i1)」をプロットしました．このプロットがR_Z2の周波数特性を表しています．図7のプロットより抵抗は6.8Ωとなり，式6を使って机上計算した「R_Z2=6.5Ω」とほぼ同じです．これより式6によるR_Z2の近似値とシミュレーション結果は，ほぼ等しいことが確認できました．

図7　図6のシミュレーション結果
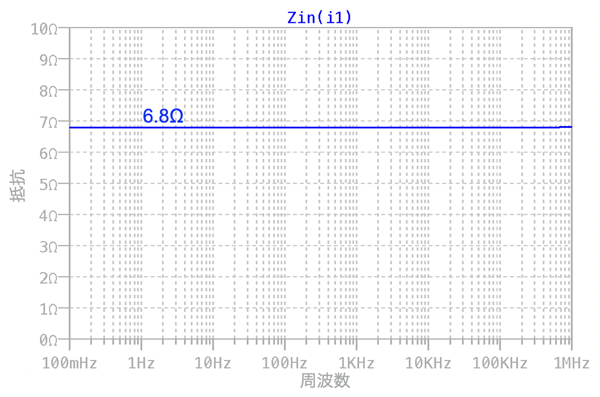
低周波の抵抗は6.8Ω．

●エミッタ・フォロワ回路の周波数特性
　図1のドット・コマンドは「.ac oct 20 0.1 1Meg」であり，図4，図6と同じ周波数掃引の小信号AC解析になります．
　図8は，図1のOUTのゲインと位相をプロットしました．周波数が約400Hz以上は，ハイ・パス・フィルタの通過域となります．

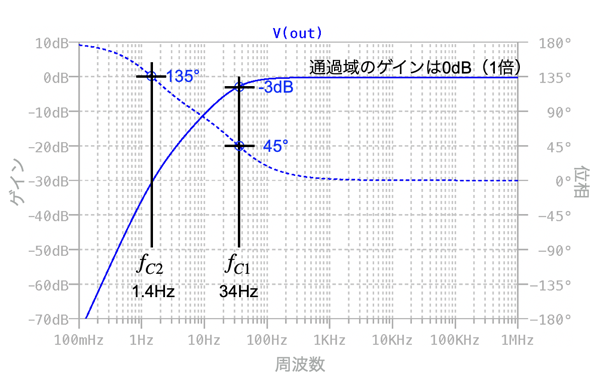
図8　図1のシミュレーション結果 f_C1=34Hz，f_C2=1.4Hzとなる．

　通過域のゲインは，1倍で位相が0°ですので，出力信号は入力信号と同相で振幅が同じになるバッファ回路として動作しています．コーナ周波数はゲインが-3dBで位相が45°進んだ周波数ですので34Hzとなります．この周波数は解答で机上計算した「f_C1=32Hz」とほぼ同じで，コーナ周波数は式4のf_C1で決まることが分かります．式7のf_C2で決まるコーナ周波数は，f_C1の位相から90°進んだ135°の位相になる周波数とみなせるので，図8では1.4Hzになります．この周波数は解答で机上計算した「f_C2=1.6Hz」とほぼ同じであることが分かります．
　以上のように，入力側のC₁と出力側のC₂で交流結合したエミッタ・フォロワ回路のコーナ周波数は，C₂をショートしてC₁と回路の抵抗で決まるコーナ周波数と，逆にC₁をショートしてC₂と回路の抵抗で決まるコーナ周波数のどちらか高い方になります．コーナ周波数は，コンデンサの容量とテブナン等価抵抗で計算できます．テブナン等価抵抗を検討するとき，「ベースからエミッタ側に付く抵抗を見ると（1+β）倍大きく見える」，「エミッタからベース側に付く抵抗を見ると（1+β）倍小さく見える」の近似値を用います．この等価抵抗は「.NET」コマンドのシミュレーションで調べることができます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice7_008.zip

●データ・ファイル内容
common collector amplifier.asc：図1の回路
common collector amplifier.plt：図1のプロットを指定するファイル
common collector amplifier RZ1.asc：図4回路
common collector amplifier RZ1.plt：図4のプロットを指定するファイル
common collector amplifier RZ2.asc：図6の回路
common collector amplifier RZ2.plt：図6のプロットを指定するファイル