LCR共振回路のQと素子定数の関係

図1は,コイル(L1)とコンデンサ(C1)および抵抗(R1)で構成されたLCR並列共振回路です.この共振回路に,交流電流源(I1)を接続して,インピーダンス特性を調べます.この共振回路の特性の説明文として,誤っているのは(a)~(d)のどれでしょう?
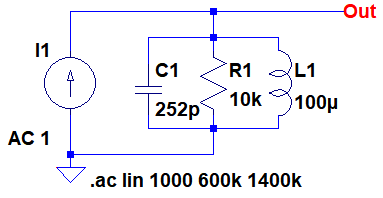
それぞれの素子の特性は,理想とします.
(a) R1の値を2倍にすると,Qは2倍になる
(b) R1の値を1/2にすると,Qは1/2になる
(c) L1の値を2倍,C1の値を1/2にするとQは2倍になる
(d) C1の値を2倍,L1の値を1/2にするとQは2倍になる

Q(Quality factor)は,共振回路の鋭さを表すもので,共振周波数を帯域幅で割ったものになります.また,LCR並列共振回路のQは,抵抗と,他の素子の共振周波数でのインピーダンスの比となることを考えれば,答えが分かります.
LCR並列共振周波数のQは,共振周波数をfとすると「Q=2πfCR」もしくは「Q=R/(2πfL)」と表すことができます.つまり,RとCの値に比例し,Lの値に反比例します.Rに比例することから,(a)と(b)は正しいことが分かります.また,Cに比例することから,(d)も正しいことになります.一方,Lに反比例となることから,(c)は誤りであることが分かります.
●LCR並列共振回路のインピーダンス特性
図2は,図1のLCR部分だけを抜き出した並列共振回路です.図2のA,B間のインピーダンスを考えてみます.
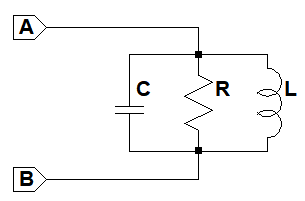
A,B間のインピーダンスを計算する.
周波数が低いときは,L1のインピーダンスが小さく,周波数が高くなると,C1のインピーダンスが小さくなることから,特定の周波数でインピーダンスが最大になることが予想されます.A,B間のインピーダンスは,3つの素子が並列になっているため,式1のようになります.
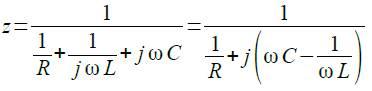 ・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・(1)
式1で分母の虚数部が0のとき「z=R」となります.虚数部が0になるのは,式2の条件を満たしたときです.
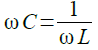 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式2を変形してωを求めると式3になります.
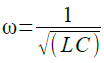 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
また,式3を周波数に変換すると式4になります.
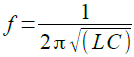 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4のfが共振周波数で,その周波数でインピーダンス最大となり,そのときの値はRと同じになります.LCR並列共振回路のQは,抵抗と,コイルおよびコンデンサの,共振周波数(f0)におけるインピーダンスの比で,式5のように表されます.
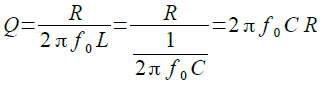 ・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・(5)
式5より,LCR並列共振回路のQは,RとCの値に比例し,Lの値に反比例することが分かります.図1の定数を代入すると,式6のように「Q=15.9」となります.
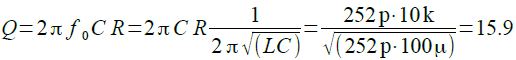 ・・・・・・・・(6)
・・・・・・・・(6)
●シミュレーション結果からカーソルを使用してQを求める
図3は,図1の回路のシミュレーション結果です.信号源が電流源となっているため,縦軸は電圧の絶対値となります.dB表示となっており,値が一番大きくなる,共振周波数のときの値は80dBとなっています.交流電流源の値が1Aとなっているため,80dBはインピーダンスの絶対値が104Ω=10kΩということで,R1の値と同じであることを表しています.
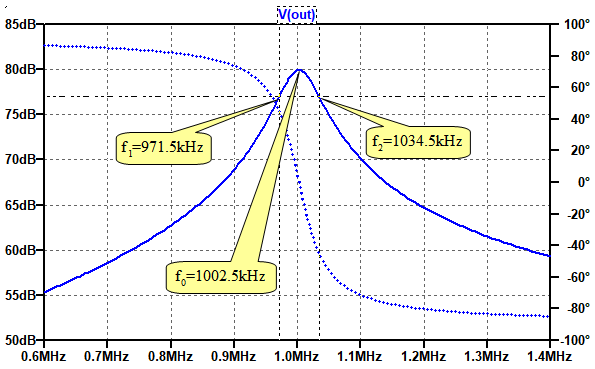
カーソルを使用して周波数を読み取り,Qを計算する.
Qは,共振周波数を帯域幅で割ったもので,共振周波数をf0とすると,式7で表されます.ここで,f1,f2はインピーダンスが1/√2(-3dB)となる周波数です.
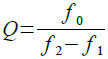 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
図3のグラフから,カーソルを使用してf0,f1,f2を読み取り,Qを計算すると,式8のように15.9になります.これは,式6で計算したものと同じです.
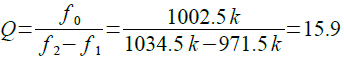 ・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・(8)
●「.MEARS」コマンドを使用してQを求める
シミュレーション結果から,カーソルを使用して周波数を読み取り,Qを計算するのはかなり大変です.そこで,LTspiceの「.MEARS」コマンドを使用して,Qの計算を自動化してみます.
「.MEARS」コマンドは,シミュレーション結果の中から,いろいろな条件を設定して,データを取り出すことができます.図4が「.MEARS」コマンドを使用して,Qを求めるための回路です.「.step」コマンドでR1の値を5kΩ,10kΩ,20kΩと変化させ,そのときのQを求めます.
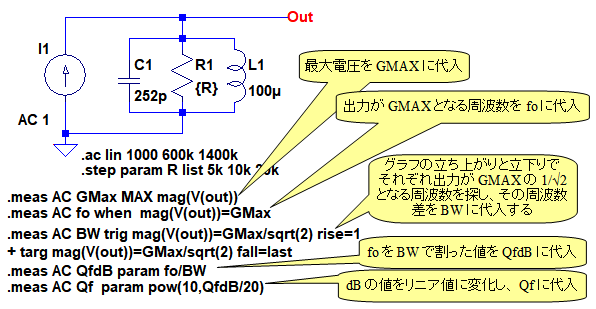
「.step」コマンドでR1の値を5kΩ,10kΩ,20kΩと変化させる.
5行の「.MEARS」コマンドでQを求めていますが,各行の意味は次のようになります.
図5がR1の値を変えた,インピーダンス特性のシミュレーション結果です.R1を変えることで波形の最大値が変化し,また波形の鋭さも変わっていることが分かります.
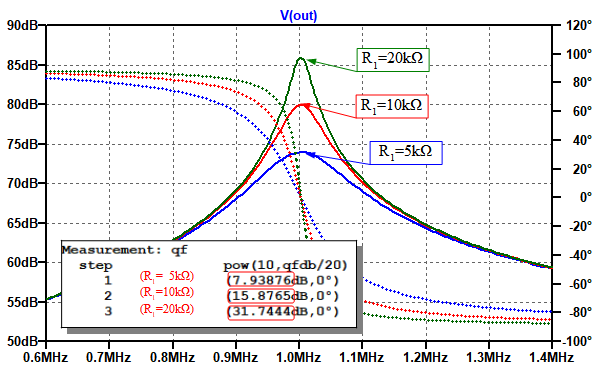
「.MEARS」コマンドの出力の中から,Qfの計算結果だけを重ねて表示している.
「.MEARS」コマンドの結果は,Ctrl+Lキーを押してエラーログを表示することで確認できます.Qfの計算結果だけを図5に重ねて表示しています.単位にdBがついてしまっていますが,値はリニアに変換したものが表示されています.R1が10kΩのとき,Qは15.9なっており,図3のカーソルで読み取った値から計算した結果と一致しています.また,R1が20kΩのときは,Qは31.7で10kΩのときの倍になり,R1が5kΩのときはQは7.9と10kΩのときの半分になっています.
●L1とC1の値を変化させたときのQを求める
次に,L1とC1の値を変化させたときにQがどのように変化するかをシミュレーションします.図6がL1とC1の値を変化させてシミュレーションするための回路です.
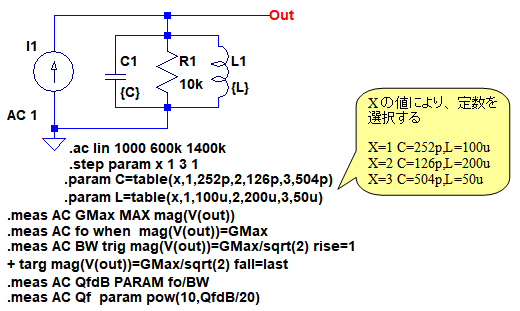
「.param」の中で,table関数を使用して定数の組み合わせを作っている.
L1の値を2倍にしたときはC1の値を1/2にする,といった組み合わせでシミュレーションするため,「.param」の中で,table関数を次のように使用しています.
.param L=table(x,1,100u,2,200u,3,50u)
このように記載すると,xの値が1のときは「C=252p,L=100u」で,Xの値が2のときは「C=126p,L=200u」となり,Xの値が3のときは,「C=504p,L=50u」となります.そして,「.step」コマンドでxを1から3まで変化させて,シミュレーションを行います
図7が図6のL1とC1の値を変化させたときのシミュレーション結果です.
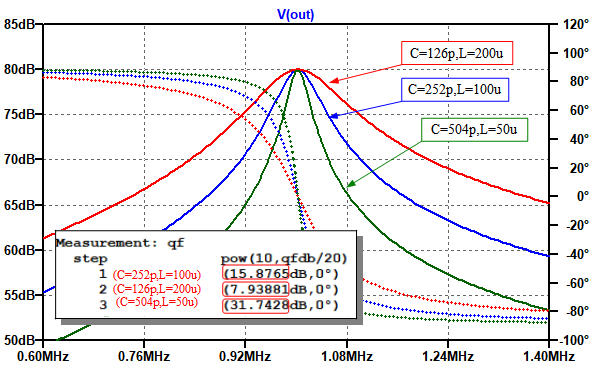
最大値は変わらずに,共振の鋭さだけが変化している.
最大値は変わらずに,共振の鋭さだけが変化しています.「C=252p,L=100u」のときと比較すると,Lを2倍にしてCを1/2した場合は,Qが7.9と半分になっています.また,Cを2倍にしてLを1/2にした場合は,Qが31.7と2倍になっています.
●LC共振回路を使用した周波数選択増幅回路
図8は,LC共振回路を使用した特定の周波数の信号を増幅するための回路です.Q1はベース接地増幅回路として動作し,LCR共振回路が負荷となっています.この回路の共振周波数は1MHzとなっているため,1MHzの信号だけを増幅することができます.
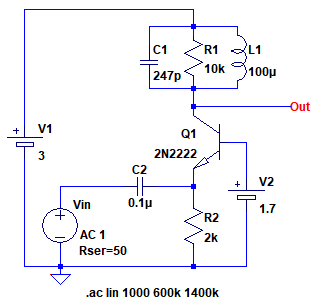
Q1はベース接地増幅回路として動作し,LCR共振回路が負荷となってる.
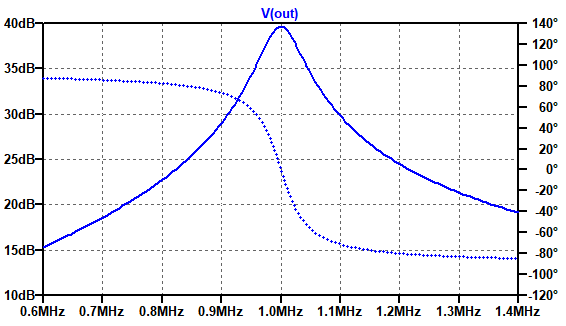
図9は図8のシミュレーション結果です.1MHzのときに約40dBのゲインがあり,他の周波数のゲインが小さくなっていることが分かります.
以上,LCR共振回路について解説しました.LCR共振回路は,ラジオやスマートホン等の無線受信器の高周波回路では,必須の構成要素となっています.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice7_005.zip
●データ・ファイル内容
RLC_Q.asc:図1の回路
RLC_Q_MEARS.asc:図4の回路
RLC_Q_MEARS_LC.asc:図6の回路
RLC_amp.asc:図8の回路
■LTspice関連リンク先
(01) LTspice ダウンロード先
(02) LTspice Users Club
(03) トランジスタ技術公式サイト LTspiceの部屋はこちら
(04) LTspice メール・マガジン全アーカイブs
(05) ◆LTspice電子回路マラソン・アーカイブs
(06) ◆LTspiceアナログ電子回路入門アーカイブs
(07) ◆LTspice電源&アナログ回路入門アーカイブs
(08) ◆IoT時代のLTspiceアナログ回路入門アーカイブs
(09) ◆オームの法則から学ぶLTspiceアナログ回路入門アーカイブs
(10) ◆LTspiceエデュケーショナル・ファイルで学ぶアナログ回路アーカイブs










