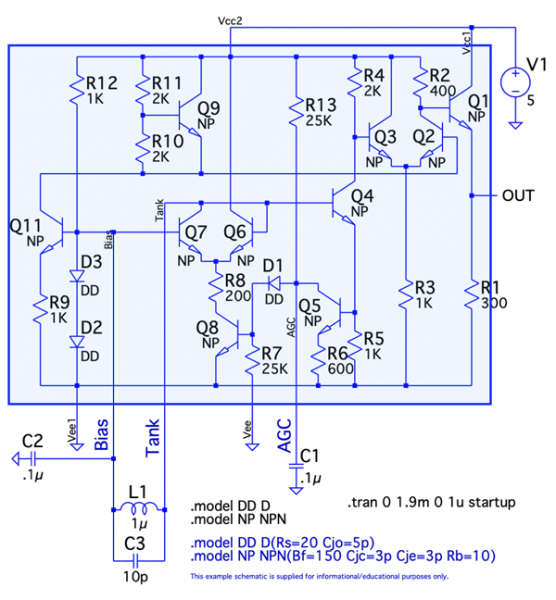
電圧制御発振器ICの回路動作

図1は,電圧制御発振器IC(MC1648)を固定周波数で動作させる発振器の回路です.ICの内部回路(青色で囲った部分)は,トランジスタ・レベルで表しています.周辺回路は,コイル(L1)とコンデンサ(C1,C2,C3)で構成され,V1が電圧源,OUTが発振器の出力となります.図1の発振周波数は,周辺回路のコイルとコンデンサからなる共振回路で決まります.発振周波数を表す式として正しいのは(a)~(d)のどれでしょうか.
(a)
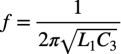 (b)
(b) 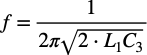
(c)
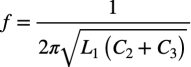 (d)
(d) 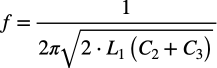
(a)の式 (b)の式 (c)の式 (d)の式

図1は,正帰還となるコイルとコンデンサの共振回路で発振周波数が決まります.(a)~(d)の式中にあるL1,C2,C3の,どの素子が内部回路との間で正帰還になるかを検討すると分かります.
周辺回路のL1,C2,C3は,Bias端子とTank端子に繋がっているので,発振に関係しそうな内部回路を絞ると,「Q11,D2,D3,R9,R12からなる回路」と,「Q6とQ7の差動アンプ」になります.
まず,Q11,D2,D3,R9,R12で構成される回路を見ると,Bias端子の電圧は「VBias=VD2+VD3=約1.4V」となり,直流電圧を生成するバイアス回路の働きであるのが分かります.「VBias=VD2+VD3=約1.4V」のVD2がダイオード(D2)の順方向電圧,VD3がダイオード(D3)の順方向電圧です.Bias端子とGND間に繋がるC2の役割は,Bias端子の電圧を安定にするコンデンサであり,共振回路とは関係がありません.これより,正解は,C2の項がある(c)と(d)の式ではありません.
次に,Q6とQ7の差動アンプを見てみます.Q6のベースとQ7のコレクタは接続しているので,Q6のベースから見るとQ7のベース・コレクタ間にあるL1とC3の並列共振回路が正帰還となります.正帰還に並列共振回路があると,共振周波数で発振します.共振したときは式1の関係となります.
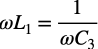 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
式1を整理すると式2になります.
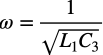 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式2より「ω=2πf」なので,共振周波数を表す式は,(a)の式となり,Tank端子が共振周波数の発振波形になります.また,Tank端子の発振波形は,Q4から後段に伝達され,Q2とQ3のコンパレータとQ1のエミッタ・ホロワを通ってOUTにそのまま伝わるので,OUTの発振周波数も(a)の式となります.
●MC1648について
図1は,電圧制御発振器のMC1648をトランジスタ・レベルで表し,周辺回路を加えた回路です.MC1648は,固定周波数の発振器や電圧制御発振器として使われます.主な特性を挙げると,発振周波数は,周辺回路のLC共振回路で決まります.発振振幅は,AGC(Auto Gain Control)により時間が経過すると一定になります.OUTからは発振波形をデジタルに波形整形して出力します.OUTの信号はデジタル回路のクロック信号として使われます.
●ダイオードとトランジスタの理想モデル
図1のダイオードとトランジスタは理想モデルとしました.理想モデルを用いると寄生容量の影響を取り除いたシミュレーション結果となり,波形の時間変化が理解しやすくなります.理想モデルとするため「.model」ステートメントは以下の指定をします.
.model DD D ;理想ダイオードのモデル
.model NP NPN;理想NPNトランジスタのモデル
●内部回路の動作について
内部回路の動作は,シミュレーションした波形で解説します.図2は,図1のシミュレーション結果で,V1の電源が立ち上がってから発振が安定するまでの変化を表しています.
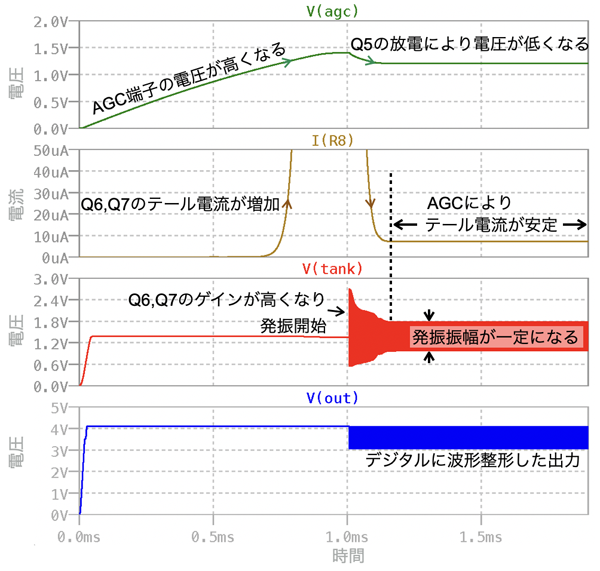
図2で,図1の内部回路を解説します.V1の電源が5Vに立ち上がると,AGC端子の電圧は,電源からR13を通ってC1に充電された電圧なので,図2のV(agc)のプロットのように時間と共に電圧が高くなります.
AGC端子の電圧が高くなると,Q8,D1,R7からなるバイアス回路が動き,Q8コレクタからバイアス電流が流れます.バイアス電流は,R8の電流なので,図2のI(R8)のプロットのように差動アンプ(Q6,Q7)のテール電流が増加します.
差動アンプは,テール電流が増えるとゲインが高くなります.ゲインが高くなると図2のV(tank)のプロットのようにTank端子とBias端子間の並列共振回路により発振し,Q4のベースに発振波形が伝わります.発振波形はQ4からQ5のベースに伝わり,発振振幅が大きいとC1からQ5のコレクタを通って放電するのでAGC端子の電圧は低くなります.この自動制御によってテール電流が安定し,V(tank)の発振振幅は一定となります.
Q2とQ3はコンパレータで,Q2のベース電圧(VB2)は,R10,R11,Q9により「VB2=V1-2*VBE9」の直流電圧になります.このVB2の電圧がコンパレータのしきい値となります.一方,Q4ベースの発振波形はQ4のコレクタ電流変化となり,R4で電圧に変換されてQ3のベース電圧となります.Q2とQ3のコンパレータで比較した電圧波形がQ1のエミッタ・ホロワからOUTに伝わり,図2のV(out)のように,デジタルに波形整形した出力になります.
●発振波形とデジタル波形を確認する
図3は,図2のシミュレーション終了間際の200ns間について,Tank端子とOUT端子の電圧をプロットしました.Tank端子は正弦波の発振波形となり,発振周波数をカーソルで調べると50MHzとなります.式1を使って,発振周波数を計算すると,図1の「L1=1μH」,「C3=10pF」より「f=50MHz」ですので机上計算とシミュレーションの値が一致することが分かりました.そして,OUTの波形は,発振波形をデジタルに波形整形した出力になることが確認できます.
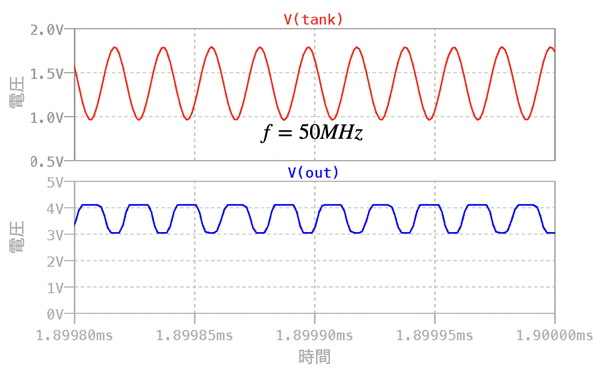
シミュレーション終了間際の200ns間をプロットした.
●具体的なデバイス・モデルによる発振周波数の変化
式1は,ダイオードやトランジスタが理想で,内部回路が発振周波数に影響しないときの理論式です.しかし,実際はダイオードとトランジスタは理想ではないので,式1の発振周波数から誤差が生じます.ここでは,ダイオードとトランジスタへ具体的なデバイス・モデルを与えてシミュレーションし,図3の理想モデルの結果と比較します.
図1のダイオードとトランジスタへ具体的なデバイス・モデルを指定する例として,次の「.model」ステートメントに変更します.このデバイス・モデルはLTspiceのEducationalフォルダにある「MC1648.asc」中で使用しているものです.図1ではコメント・アウトしているので,理想のデバイス・モデルと入れ変えることによりシミュレーションできます.
.model DD D(Rs=20 Cjo=5p)
.model NP NPN(Bf=150 Cjc=3p Cje=3p Rb=10)
図4は,具体的なデバイス・モデルへ入れ替えたシミュレーション結果で,Tank端子とOUT端子の電圧をプロットしました.図3の理想モデルを使用したシミュレーション結果と比べると,図4の発振周波数は,34MHzとなり,理想モデルの50MHzより周波数が低下することが分かります.また,OUTの波形は図3の波形より歪んだ結果となります.このようにLTspiceを用いて理想モデルと具体的なデバイス・モデルの差を調べることができます.
発振周波数が式1から誤差が生じる原因は,他にもあり,周辺回路のリードのインダクタンスや浮遊容量が挙げられます.実際に基板に回路を作ったときは,これらの影響も考慮しなければなりません.
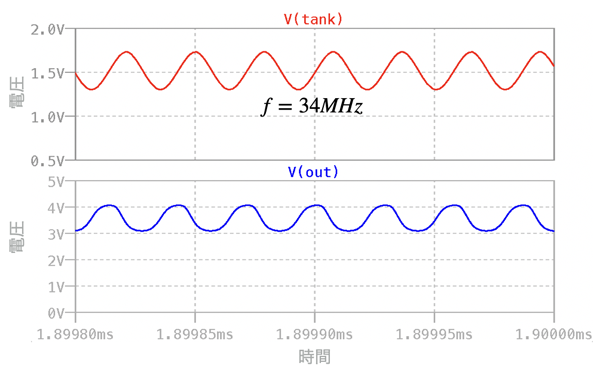
図3と比較すると,発振周波数が変わり,OUTの波形が歪んでいる.
●バリキャップを使った電圧制御発振器
図5は,周辺回路にバリキャップ(可変容量ダイオード)を使った電圧制御発振器で,図1のC3をバリキャップ(D4,D5)に変えた回路です.バリキャップは,V2の直流電圧で静電容量が変わるので共振周波数が変わります.共振周波数は発振周波数なので,V2の電圧で周波数が変わる電圧制御発振器になります.
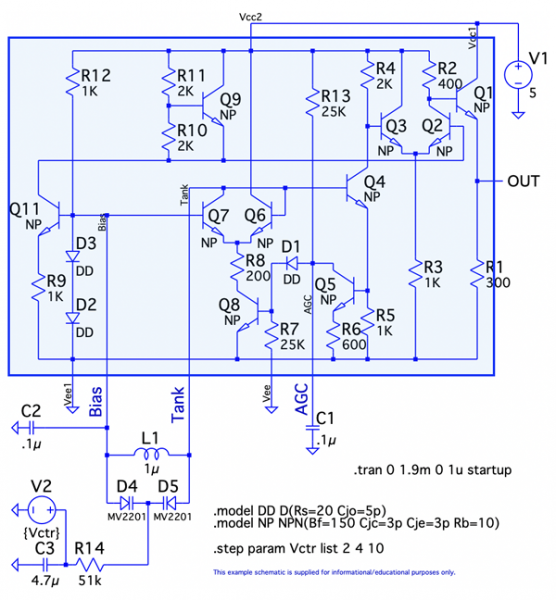
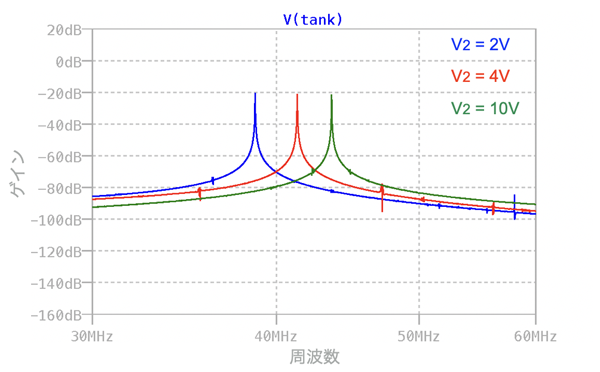
注意点としてV2は,約1.4V以上の電圧にします.理由として,バリキャップは,逆バイアス電圧に応じて容量が変わるので,V2の電圧がBias端子とTank端子の電圧より高くしないと逆バイアスにならないからです.Bias端子とTank端子の直流電圧が約1.4Vなので,V2はそれ以上の電圧ということになります.図5では「.stepコマンド」で,V2の電圧を2V,4V,10Vと変えて発振周波数を調べています.
バリキャップについては「バリキャップ(varicap)の使い方」に詳しい記事がありますので,そちらを参考にしてください.
●電圧制御発振器のシミュレーション
図6は,図5のシミュレーション結果で,シミュレーション終了間際の200ns間についてTank端子の電圧をプロットしました.図6よりV2の電圧で発振周波数が変わることが分かります.
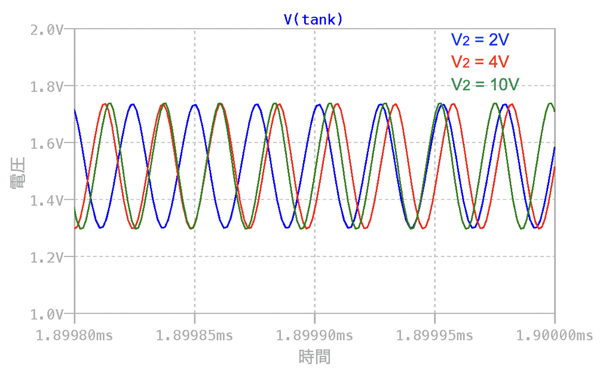
シミュレーション終了間際の200ns間をプロットした.
図7は,V2による周波数の変化を分かりやすく表示するため,図6をFFTした結果です.山がピークになるところが発振周波数ですので,V2の電圧で発振周波数が変わる電圧制御発振器になることが分かります.
以上,解説したようにMC1648は周辺回路のコイルとコンデンサの共振周波数で発振し,OUTの信号は高周波のクロック信号として使います.共振回路のコンデンサをバリキャップに変えることにより,電圧制御発振器として動作します.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice6_046.zip
●データ・ファイル内容
MC1648.asc:図1の回路
MC1648.plt:図1のプロットを指定するファイル
MC1648 VCO.asc:図5の回路
MC1648 VCO.plt:図5のプロットを指定するファイル
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










