温度による出力電圧変化の少ない基準電圧源

図1は,温度による出力電圧の変化が少ない,バンドギャップ・リファレンスの温度特性をシミュレーションする回路です.トランジスタQ3は,Q4の10倍のサイズとなっています.
また,27℃のとき,B点の電圧は714mVで,B点の温度による電圧変化率は-1.49mV/℃でした.温度によるA点の電圧の変化が一番少ないのは,R2の値を(a)~(d)のどの値にしたときでしょうか.
ただし,トランジスタの電流増幅率やアーリ電圧は十分大きく,その影響は無視できるものとします.
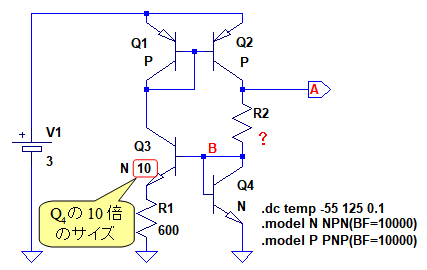
温度によるA点の電圧の変化が一番少ないのはどれ?
(a) 3.5kΩ (b) 4.5kΩ (c) 5.5kΩ (d) 6.5kΩ

R2の値を求めるためには,R2に流れる電流を計算する必要があります.その電流はQ3とQ4のサイズの比とR1から計算することができます.そして,B点の温度による電圧変化と,R2の電圧の温度に対する変化が,打ち消しあうように,R2の値を選びます.
図1の回路で,Q1とQ2はカレント・ミラーを構成しているため,Q1とQ2の電流は同じになります.さらに,Q3とQ4の電流も同じになります.この電流の値(I)は,Q3とQ4のサイズの比をMとすると「I=Vt*ln(M)/R1」という式で計算することが可能です.この電流は正の温度係数を持ち,その係数は0.33μA/℃です.R2に発生する電圧は,この電流とR2を掛けたものです.A点の電圧は,B点の電圧にR2の電圧を足したものなので,R2の電圧の温度による電圧変化率が1.49mV/℃となれば,A点の温度による電圧変化がなくなります.つまり,「R2=1.49mV/0.33μA=4.5kΩ」から求められます.
●電源電圧に依存しない電流源回路
図1の回路で,トランジスタに流れる電流は,電源電圧に依存しません.そのため,一定の電流を供給する定電流源回路としても使用されます.その一定の電流が,どのように決まるかを,図2を使用して解析します.
まず,Q3のコレクタ電流(I)がQ1に流れます.Q1とQ2はカレント・ミラーを構成しているので,Q2のコレクタ電流もQ1と同じ値になります.Q2のコレクタ電流がQ4に流れるため,Q4の電流はQ2と同じです.つまり,4つのトランジスタの電流は,すべて同じIという値になります.
ここで,B点の電圧に着目して式を立てます.B点の電圧(VB)はQ4のベース・エミッタ間電圧と同じなので,式1で表されます.
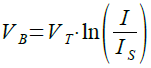 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
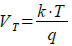 のISはトランジスタの逆方向飽和電流,kはボルツマン定数で1.38×10-23 [J/K],qは電子電荷で1.6×10-19 [C],Tは絶対温度で27℃のとき300[K].
のISはトランジスタの逆方向飽和電流,kはボルツマン定数で1.38×10-23 [J/K],qは電子電荷で1.6×10-19 [C],Tは絶対温度で27℃のとき300[K].
また,B点の電圧は,Q3のベース・エミッタ間電圧とR1の電圧降下を足したものでもあります.Q3のサイズがQ1のM倍だとすると,式2が成立します.
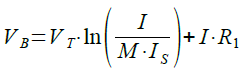 ・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・(2)式1および式2からIを求めると,式3になります.
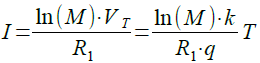 ・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・(3)式3には,電源電圧の項がないため,電源電圧に依存しないことが分かります.また,式3を見ると分かるように絶対温度Tに比例し,正の温度係数を持っていることが分かります.なお,この回路は電流値が0でも安定してしまう可能性があります.つまり,Q4の電流が0だとすると,B点の電圧は0Vになり,Q3に電流が流れず,Q1,Q2の電流も0で安定してしまいます.そのため,実際にこの回路を使用する場合は,きっかけとなる電流を流す,スタータ回路と呼ばれる回路を追加します.
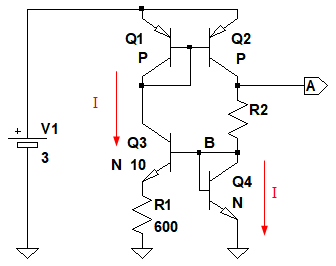
実際に使用する場合は,スタータ回路を追加する必要がある.
●温度に依存しない電圧源
図2の回路に流れる電流は,正の温度係数を持っています.一方,トランジスタのベース・エミッタ間電圧は,負の温度係数をもっています.一般的にその温度係数の値は-2mV/℃といわれていますが,素子サイズや流す電流値,流す電流の温度係数によって多少変化します.
図1の回路では,この値が-1.49mV/℃でした.この負の温度係数をもった電圧と正の温度係数を持った電圧を,適切な比率で加算すれば,温度に対する電圧変化の少ない,電圧を得ることができます.図2の回路で,R2に発生する電圧(VR2)は式4で表されます.
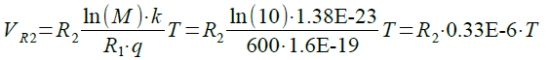 ・・・・・(4)
・・・・・(4)
式4よりVR2は,正の温度係数を持ち,その温度係数の値は「R2*0.33μV/℃」であることが分かります.この温度係数を1.49mV/℃となるように,R2の値を設定すれば,図2のA点の電圧の温度に対する変化を小さくすることができます.これを数式にしたものが式5です.
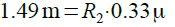 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
また,式5を変形すると,式6のようにR2の値を求めることができます.
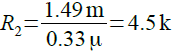 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
図3は,R2の値を4.5kΩとしたときの温度特性をシミュレーションする回路です.温度を-55℃から125℃まで,0.1℃ステップで変化させて特性を調べます.
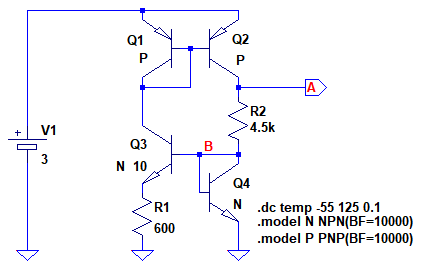
R2の値を4.5kΩとして,トランジスタの温度係数を打ち消している.
図4は,図3のシミュレーション結果です.上段がA点,B点およびA-B間の電圧です.B点は,Q4のベース・エミッタ間電圧で,高温になるほど小さくなります.一方A-B間の電圧は,高温になるほど大きくなっています.この二つの電圧を加算したA点の電圧は,温度による電圧変化が非常に小さいことが分かります.
中段は,抵抗に流れる電流を温度で微分したものです.温度で微分することで温度係数が求められますが,値は式4で計算した値と同じ,0.33μA/℃となっています.
下段がB点の電圧を温度で微分したものです.温度により,若干変化していますが,27℃近辺では1.49mV/℃となっています.
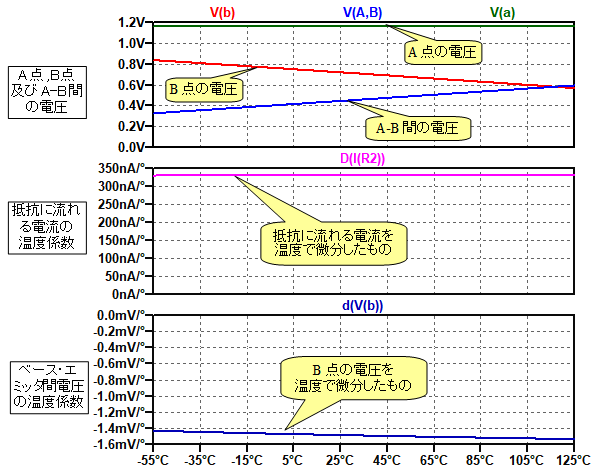
A点の電圧は温度による電圧変化が非常に小さい.
図5は,図3の回路のR2の値を「.stepコマンド」で3.5kΩ,4.5kΩ,5.5kΩ,6.5kΩと変化させたときのシミュレーション結果です.A点の電圧は,R2の値を4.5kΩにしたときが,最も温度による電圧変化が小さくなっています.また,R2の値が4.5kΩよりも大きいと正の温度係数になり,小さいと負の温度係数になることも分かります.
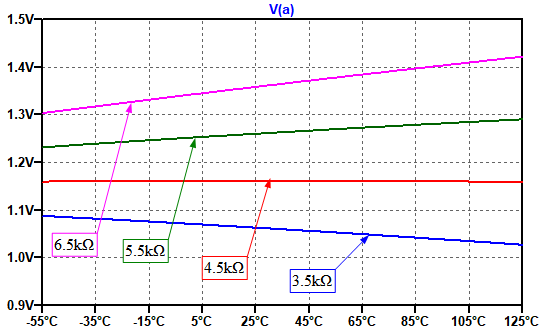
R2の値を4.5kΩにしたときが,最も温度による電圧変化が小さい.
●いろいろなバンドギャップ・リファレンス回路
バンドギャップ・リファレンス回路には,いろいろな改良を加えた,多くの種類の回路があります.図6はLTspiceのサンプル・ファイル(ドキュメント\LTspiceXVII\examples\Educational\BandGaps.asc)です.それぞれ,トランジスタのアーリ効果や負荷電流による特性の変化の仕方が異なります.
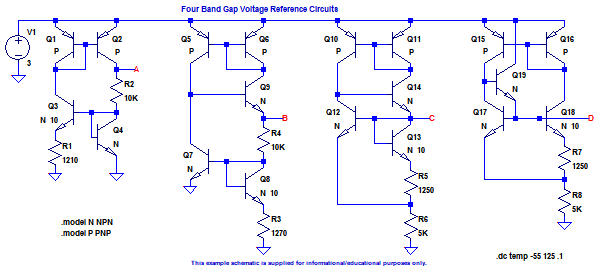
バンドギャップ・リファレンス回路には,いろいろな改良を加えた,多くの種類の回路がある.
図7は,図6の4つの回路のシミュレーション結果です.上段,下段ともにそれぞれの出力端子の電圧を表示していますが,下段は縦軸のレンジを拡大したものです.いずれの回路も,温度による出力電圧の変化が小さいことが分かります.
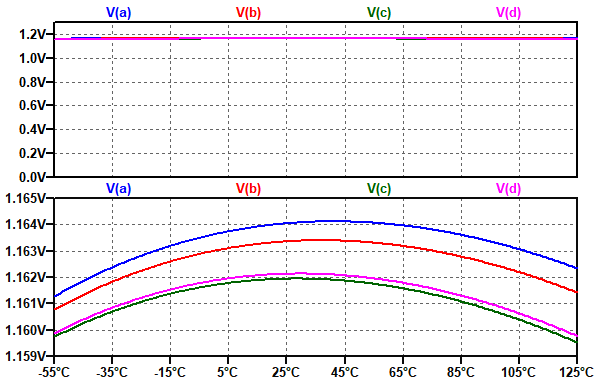
いずれの回路も,温度による出力電圧の変化が小さい.
以上,バンドギャップ・リファレンス回路について解説しました.バンドギャップ・リファレンス回路は図6の回路以外にも非常に多くの回路形式が考案されています.別の回路形式に関しては,「LTspice電源&アナログ回路入門017 ―― バンドギャップ・リファレンスの温度補償」を参照して下さい.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice6_041.zip
●データ・ファイル内容
BandGap_Iref.asc:図3の回路
BandGap_stepR.asc:図5をシミュレーションする回路
BandGaps.plt:図6の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










