フィルタ設計の一連の流れ

『LTspice Users Club』のWebサイトはこちら

■問題
フィルタ ― 中級

平賀　公久　Kimihisa Hiraga

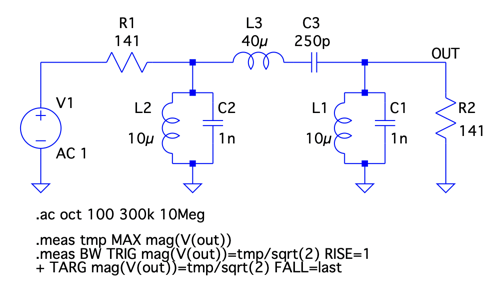
　図1は，抵抗やコイル，コンデンサを使ったフィルタ回路で，V₁が入力でOUTが出力です．図1の出力波形はどのようになり，そのフィルタの名前は何でしょうか．図2の(a)～(d)の中から選んで下さい．

図1　抵抗やコイル，コンデンサを使ったフィルタ回路

図2　図1の出力波形

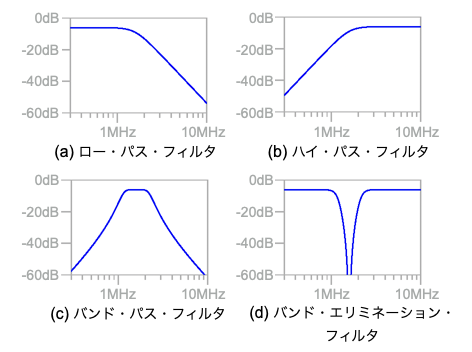
(a) ロー・パス・フィルタ
(b) ハイ・パス・フィルタ
(c) バンド・パス・フィルタ
(d) バンド・エリミネーション・フィルタ

■ヒント

　コイルは，周波数に比例した抵抗(誘導性リアクタンス)で，直流では0Ω，無限大周波数では無限大の抵抗と見なせます．また，コンデンサは，周波数に反比例した抵抗(容量性リアクタンス)で，直流では無限大の抵抗，無限大周波数では0Ωと見なせます．低周波，高周波，中間の周波数において，V₁(入力)からOUT(出力)までの交流信号の伝わり方を検討すると分かります．

■解答

(c) バンド・パス・フィルタ

　まず，低周波のときの入力から出力までの交流信号の伝わり方を検討します．コイルは周波数に比例した抵抗と見なせ，また，コンデンサは周波数に反比例した抵抗と見なせます．低周波になるにつれてC₃の抵抗が大きくなるので，V₁の交流信号はOUTに伝わりにくくなります．また，L₁とL₂は低周波になるにつれて抵抗が小さくなるので，V₁の交流信号はOUTに伝わりにくくなります．これより，V₁の周波数が低くなるとOUTに現れる交流信号は減衰し，VOUT/V₁のゲインは低下します．
　高周波になると同じことがL₃とC₁とC₂に起こり，高周波になるにつれてL₃の抵抗が大きくなるので，V₁の交流信号はOUTに伝わりにくくなります．そして，C₁とC₂の抵抗は小さくなるので，V₁の交流信号はOUTに伝わりにくくなります．したがって，V₁の周波数が高くなるとOUTに現れる交流信号は減衰し，VOUT/V₁のゲインは低下します．
　中間の周波数では，コイルとコンデンサの抵抗が近づいて，V₁の交流信号がOUTに伝わる周波数帯があります．この周波数帯のVOUT/V₁のゲインは，周波数に応じて変化します．
　以上より，低周波と高周波の交流信号を減衰させ，中間の周波数の交流信号を通過させるのはバンド・パス・フィルタです．なので，解答は，(c)のバンド・パス・フィルタとなります．

■解説

●ロー・パス・フィルタからバンド・パス・フィルタへの周波数変換
　フィルタの設計では，基準となるロー・パス・フィルタから，周波数変換と呼ばれる技法で，ハイ・パス・フィルタやバンド・パス・フィルタ，バンド・エリミネーション・フィルタを作ります．ここでは，ロー・パス・フィルタからバンド・パス・フィルタへの周波数変換について解説します．
　図3は，ロー・パス・フィルタで使っているコイルとコンデンサをバンド・パス・フィルタの素子へ周波数変換したものです．

図3　コイルとコンデンサの周波数変換

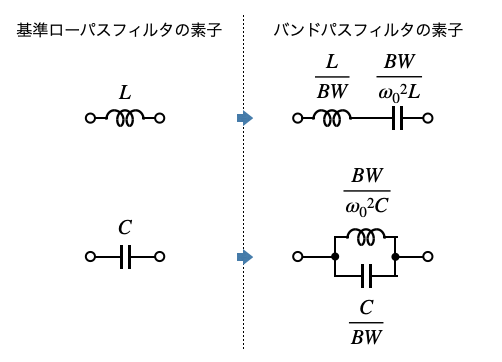
　図3よりロー・パス・フィルタで使っているコイルを，コイルとコンデンサの直列に変換するとバンド・パス・フィルタの素子になります．
　また，コンデンサをコンデンサとコイルの並列に変換するとバンド・パス・フィルタの素子になります．変換したときの素子値は，図3中の関係を用います．ここで，BWは，式1で表した帯域幅で，角周波数で表した低周波側のコーナ周波数(ω₁)と高周波側のコーナ周波数(ω₂)間の周波数差となります．

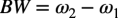・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　また，ω₀は，式2で表した中心周波数で，ω₁とω₂の相乗平均となります．

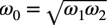・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

●具体的な周波数変換例
　図4(a)は，バタワース特性の基準ロー・パス・フィルタで，コーナ周波数が「ωC=1rad/s」です．これを図3の周波数変換を使って図4(b)のバンド・パス・フィルタに変換しました．具体的には図4(a)のL₄は図4(b)の「L₃とC₃の直列」になります．同様に図4(a)のC₅は図4(b)の「L₂とC₂の並列」，図4(a)のC₄は図4(b)の「L₁とC₁の並列」となります．

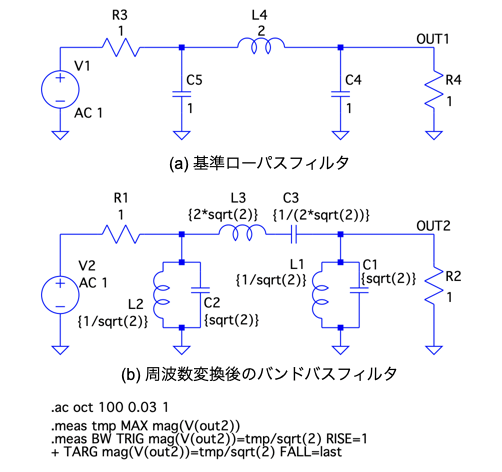
図4　基準ロー・パス・フィルタからバンド・パス・フィルタへの周波数変換．
(a)は基準ロー・パス・フィルタ
(b)は周波数変換後のバンド・パス・フィルタ

　図4(b)の素子値は，図3中の関係を用い，バンド・パス・フィルタの条件として中心周波数「ω₀=1rad/s」，低周波側のコーナ周波数は「ω₁=(1/√2)ω₀」，高周波側のコーナ周波数は「ω₂=(√2)ω₀」とし，帯域幅を「BW=(1/√2)ω₀」となるようにしました．図4(b)の素子値は「L₃=2√2 H」，「C₃=1/(2√2) F」，「L₁=L₂=1/√2 H」，「C₁=C₂=√2 F」となります．
　図5は，図4のシミュレーション結果で，周波数特性をプロットしました．図4(a)は赤のプロットでコーナ周波数が1rad/sのロー・パス・フィルタです．図4(b)は青のプロットでバンド・パス・フィルタになっているのが分かります．

図5　図4の周波数特性をプロット

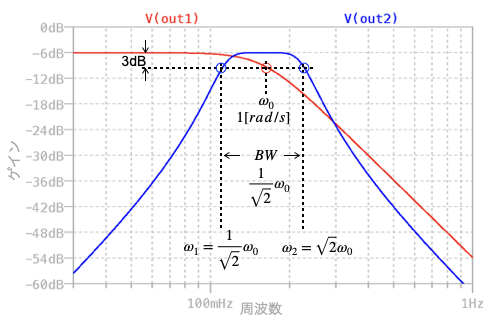
　図6は「.measコマンド」を使い，図4(b)の低周波側のコーナ周波数(f₁)，高周波側のコーナ周波数(f₂)，帯域幅(BW)を自動測定した結果です．測定したf₁，f₂，BWを角周波数に直すと「ω₁=1/√2 rad/s」，「ω₂=√2 rad/s」，「BW=1/√2rad/s」，また，中心周波数は式2より「ω₀=1 rad/s」となり，先ほど設定したバンド・パス・フィルタの条件と一致していることが分かります．このように，周波数変換によりロー・パス・フィルタをバンド・パス・フィルタへ変換できるのが分かります．

図6　図4の.measの結果
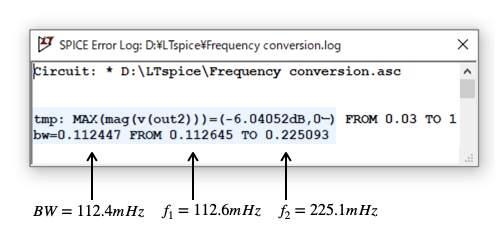
コーナ周波数，バンド幅が分かる．

●スケーリング
　図4(b)の周波数変換後のバンド・パス・フィルタの素子値は，大きなコイルとコンデンサの値なので実際には作れません．したがって，現実的な素子値にするためにスケーリングをおこないます．スケーリングには周波数を調整する「周波数スケーリング(k_f)」と，素子値を調整する「インピーダンススケーリング(k_m)」があります．
　コイルのスケーリング後の素子値をL_scale，スケーリング前の素子値をL_oldとすると式3となります．

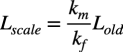・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　コンデンサのスケーリング後の素子値をC_scale，スケーリング前の素子値をC_oldとすると式4となります．

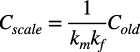・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　抵抗のスケーリング後の素子値をR_scale，スケーリング前の素子値をR_oldとすると式5となります．

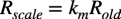・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　具体的なスケーリング例として，図4(b)のバンド・パス・フィルタの中心周波数を「ω₀=1 rad/s」から「ω₀=10M rad/s」にすると，周波数スケーリング(k_f)は式6の値となります．

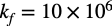・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　また，図4(b)の「C₁=C₂=√2F」の大きな容量を現実的な「C₁=C₂=1nF」にすると，インピーダンス・スケーリング(k_m)は式4の関係と式6の値を使って式7となります．

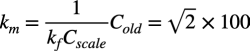・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式6の周波数スケーリング(k_f)と式7のインピーダンススケーリング(k_m)が決まったので，残りの素子を式3，式4，式5を用いて求めると，「L₃=40μH」，「C₃=250pF」，「L₁= L₂=10μH」，「R₁=R₂=141Ω」となり，この素子値が図1の値となります．

●スケーリング後の回路をシミュレーションで検証する
　図7は，図1をシミュレーションして周波数特性をプロットしました．スケーリング後の周波数特性は図5(青のプロット)の山の形は変わらないまま高周波側にシフトしたバンド・パス・フィルタになっているのが分かります．このプロットが図2(c)となります．

図7　図1の周波数特性をプロット

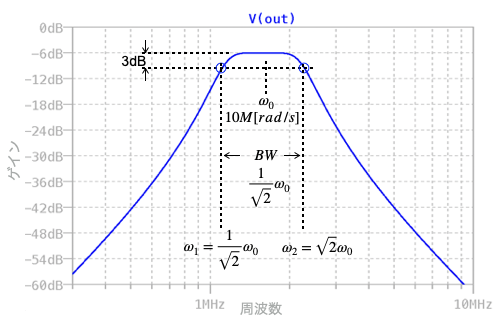
　図8は「.measコマンド」で，図1の低周波側のコーナ周波数(f₁)，高周波側のコーナ周波数(f₂)，帯域幅(BW)を自動測定した結果です．測定したf₁，f₂，BWを角周波数で表すと「ω₁=(1/√2)×10×10⁶ rad/s」，「ω₂=√2×10×10⁶ rad/s」，「BW=(1/√2)×10×10⁶ rad/s」，「ω₀=1×10×10⁶ rad/s」となります．図6のスケーリング前と比べると周波数スケーリングの10×10⁶倍になります．

図8　図1の.measの結果
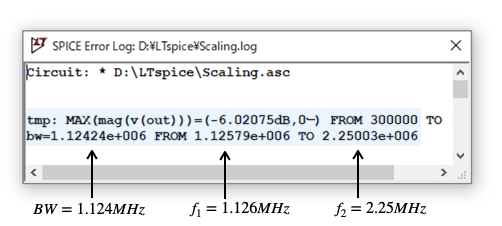
コーナ周波数，バンド幅は10×10⁶倍シフトしている．

　以上，ここまでが，問題のロー・パス・フィルタから周波数変換とスケーリングを使用し，バンド・パス・フィルタを設計した解説でした．次は，このように設計したバンド・パス・フィルタを量産する場合，部品のばらつきによる特性変動が仕様内に納まるかをモンテカルロ解析で調べて見ます.

●モンテカルロ解析
　図9は，LTspiceのEducationalフォルダにある「MonteCarlo.asc」の回路です．コイルとコンデンサと抵抗の素子値は，図1と同じで，モンテカルロ解析の条件が加わっています．モンテカルロ解析は，部品の素子値を許容誤差の分布内で乱数により変動させて，数多くのシミュレーションを繰り返すことにより特性の変動を調べるときに使います．

図9　図1のMonte Carloシミュレーションをする回路
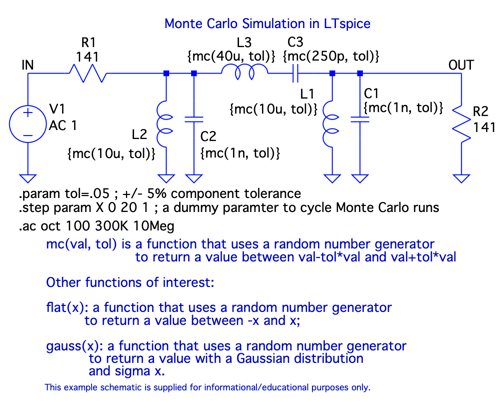
コイルとコンデンサを一様分布で±5％としている．
（LTspiceXVII\examples\Educational\MonteCarlo.asc）

　図9のコイルとコンデンサの素子値は，次のmc関数で公称値と許容誤差を与えています．

　mc(x,y):x*(1+y)値から x*(1-y) 値間で一様分布の乱数を発生

　図9のL₃を例にすると，mc(40μ，tol)となっており，変数のtolは「.param」で「tol=0.05」と指定されています．これは，コイルの公称値が「40μH」で許容誤差が「±5%」となります．図9のコイルとコンデンサの許容誤差は全て「公称値±5%」となります．モンテカルロ解析の回数は「.stepコマンド」のダミー変数Xで指定します．図9では「.step param X 0 20 1」なので，Xが0から20まで1ステップで計21回実行します．
　図10は，図9のモンテカルロ解析を実行して周波数特性をプロットしました．図7と比べると周波数特性が変動していることが分かります．このように部品の素子値を許容誤差内で変動させ，目標とする特性を満足するかの確認をおこないます．

図10　図9の周波数特性をプロット
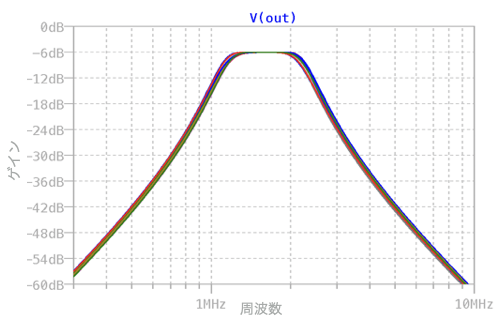
素子値を変化させた21回のシミュレーション結果．

　過去のメルマガには，ロー・パス・フィルタからハイ・パス・フィルタを作った記事「正しく周波数変換とスケーリングした回路はどっち？」もあります．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice6_036.zip

●データ・ファイル内容
Scaling.asc：図1の回路
Scaling.plt：図1のプロット指定するファイル
Frequency conversion.asc：図4の回路
Frequency conversion.plt：図4のプロット指定するファイル
MonteCarlo.asc：図9の回路
MonteCarlo.plt：図9のプロット指定するファイル