エミッタ接地アンプの周波数特性

■問題
トランジスタ応用 ― 中級

平賀　公久　Kimihisa Hiraga

　図1は，NPNトランジスタを使ったエミッタ接地アンプです．この回路は，交流の信号だけ増幅し，直流の信号を増幅しません．交流の信号は，低周波側のコーナ周波数(f_CL)から高周波側のコーナ周波数(f_CH)までとなります．C₁，C₂，C₃のコンデンサは，f_CLとf_CHのコーナ周波数に影響を及ぼします．その説明として正しいのは，(a)～(d)のどれでしょうか．

図1　NPNトランジスタを使ったエミッタ接地アンプ
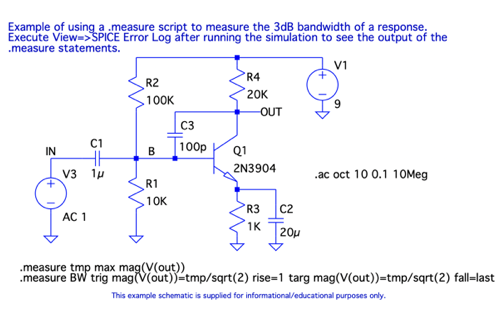
オリジナルの回路にBノードのラベルを加えています．
ドキュメント\LTspiceXVII\examples\Educational\MeasureBW.asc

(a)　C₁とC₂はf_CL，C₃はf_CHに影響する
(b)　C₁とC₃はf_CL，C₂はf_CHに影響する
(c)　C₁はf_CL，C₂とC₃はf_CHに影響する
(d)　C₃はf_CL，C₁とC₂はf_CHに影響する

■ヒント

　コンデンサは，低周波でオープン，高周波でショートと考えることができます．C₁，C₂，C₃のコンデンサがオープン，またはショートしたときの信号の伝わり方や回路の動きを検討すると分かります．

■解答

(a)　C₁とC₂はf_CL，C₃はf_CHに影響する

　C₁は，低周波でオープンとすると信号を通過させず，高周波でショートになると回路中のIN(ノード)とB(ノード)が接続されて信号が通過するハイ・パス・フィルタになります．これよりC₁は低周波側のコーナ周波数(f_CL)に影響を及ぼします．
　C₂は，低周波でオープンとするとR₃がエミッタとGND間に接続している状態となります．高周波でショートになるとR₃の両端もショートになってエミッタはGNDになります．エミッタ接地アンプは，R₃があるとゲインは低くなり，R₃がショートするとゲインは高くなります．これより低周波側で低いゲイン，高周波側で高いゲインとなるハイ・パス特性になるため，低周波側のコーナ周波数(f_CL)に影響を及ぼします．
　C₃は，低周波でオープンとすると回路に影響を与えません．高周波でショートのとき，ベースとOUTが接続され，ベースの信号は増幅されずにOUTに現れるためゲインが低くなります．これより，低周波側では，回路で決まるゲイン，高周波側で低いゲインとなるロー・パス特性になるため，高周波側のコーナ周波数(f_CH)に影響を及ぼします．
　以上よりC₁，C₂，C₃のコンデンサがf_CLとf_CHのコーナ周波数に及ぼす影響は，(a)の「C₁とC₂はf_CL，C₃はf_CHに影響する」になります．　図1のエミッタ接地アンプの周波数特性は，f_CLより低くなる低周波，f_CLとf_CHの間のアンプとして使用できるゲインのある中域周波数，f_CHより高くなる高周波の3つに分けることができます．解説では，3つの周波数の応答について説明します．

■解説

●低周波応答
　図2は，図1のトランジスタを低周波π型等価回路に置き換えた小信号等価回路です．C₃の容量値は，C₁とC₂の容量値に比べると遥かに小さいので無視しています．R_Sはv_sの信号源抵抗です．この図を使って低周波でのコーナ周波数を検討します．

図2　図1の低周波における小信号等価回路

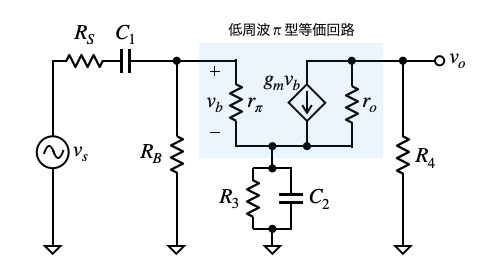
　コーナ周波数の解析で伝達関数を解くと計算量が多くなります．そこで，AC結合などで生まれる低周波のコーナ周波数は，Short-Circuit Time Constant法を使って近似値を求めます．Short-Circuit Time Constant法は，図2の電圧源(v_s)をショートにします．そして複数あるコンデンサの1つを残し，他のコンデンサは十分に低いインピーダンスになったショートとしたときのコーナ周波数を求めます．これをコンデンサの数だけ繰り返して求め，各々のコーナ周波数を加算すると，おおよそ全体のコーナ周波数になります．

●C₁による低域側のコーナ周波数
　C₁による低域側のコーナ周波数を検討するため，C₂はショートにして考えます．コーナ周波数は，時定数であるCRの積の逆数です．CがC₁の容量値，Rがテブナンの定理よりC₁に付くテブナン等価抵抗となります．図2のC₂をショートしてC₁に付くテブナン等価抵抗(R_THV1)を求めると式1になります．

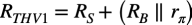・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　図2のR_Bは図1のR₁とR₂の並列抵抗ですので式2となります．

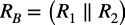・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　C₁による低域側のコーナ周波数をf_CL1とすると，式1のテブナン等価抵抗を使って式3となります．

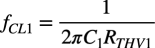・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式3の具体的な周波数を机上計算します．低周波π型等価回路のトランスコンダクタンス(Transconductance)は「g_m=I_C/V_T」で表され，図1のコレクタ電流「I_C=200μA」と熱電圧「V_T=26mV」より「g_m=7.7mA/V」となります．また，π型等価回路のベースとエミッタ間の抵抗は「r_π=β/g_m」であり，トランジスタ(2N3904)の電流増幅率は「β=312」より「r_π=41kΩ」となります．R_BはR₁とR₂の並列抵抗なので「R_B=9kΩ」となります．信号源抵抗のR_Sは，図1には無いので「R_S=0Ω」です．これらを式3へ入れると「f_CL1=22Hz」となります．

●C₂による低域側のコーナ周波数
　次にC₂による低域側のコーナ周波数を検討するため，C₁は，ショートして考えます．トランジスタは，エミッタからベース側の抵抗を見ると(1+β)倍小さく見え，これを等価エミッタ抵抗と呼びます．等価エミッタ抵抗は「r_π+(R_S||R_B)/(1+β)」となり，「等価エミッタ抵抗=131Ω」になります．コレクタ側の出力抵抗は「r_o=V_A/I_C」であり，2N3904のアーリー電圧「V_A=100V」を使うと「r_o=500kΩ」となります．r_oは等価エミッタ抵抗とR₃に比べ十分大きな値になるので無視します．これらの検討結果からC₂に付くテブナン等価抵抗(R_THV2)は，等価エミッタ抵抗とR₃の並列抵抗になり，式4となります．

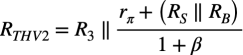・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　C₂による低域側のコーナ周波数をf_CL2とすると，式4のテブナン等価抵抗を使って式5となります．

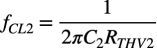・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5の具体的な周波数を机上計算すると，「f_CL1=69Hz」となります．以上の結果より，Short-Circuit Time Constant法を使って算出した，低域側のトータルのコーナ周波数の近似値は，式6となり，おおよそ「f_CL=91Hz」となります．

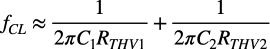・・・・・・・・・・・・・・・・・・・・・・・・(6)

●中域周波数のゲイン
　エミッタ接地アンプは，中域周波数の信号を増幅します．ここでは，中域周波数のゲインを机上計算します．中域周波数では，図1のC₁とC₂の容量は大きいのでショートと見なすことができます．小信号等価回路は図3となります．

図3　図1の中域周波数における小信号等価回路

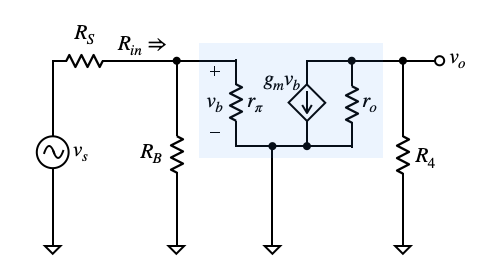
　図3の信号源抵抗(R_S)から右側をみた入力抵抗(R_in)は式7となります．式7中のR_Bは式2の通りです．

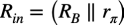・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　v_bはv_sをR_SとR_Bの抵抗で分圧した電圧なので式8となります．

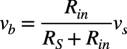・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　v_bをエミッタ接地アンプで増幅するので，出力電圧v_oは式9となります．

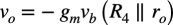・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　式8と式9より，エミッタ接地アンプのゲインは式10となります．

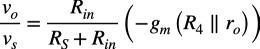・・・・・・・・・・・・・・・・・・・・・・・・(10)

　式10の具体的なゲインを机上計算します．「g_m=7.7mA/V」,「R_S=0Ω」,「r_o=500kΩ」,「R₄=20kΩ」よりゲインは「v_o/v_s=43.4dB」となります．

●高周波応答
　図4は，図1のトランジスタを高周波用のπ型等価回路に置き換えた小信号等価回路です．高周波になるとベースとエミッタ間の容量であるC_π，ベースとコレクタ間の容量であるC_BCが無視できないため，これらの容量が低周波π型等価回路に加わった等価回路となります．C₃とC_BCは並列なので1つの容量「C₃＋C_BC」と見なすことができます．C₁とC₂は図3の中域周波数の小信号等価回路と同様にショートと見なすことができます．

図4　図1の高周波における小信号等価回路

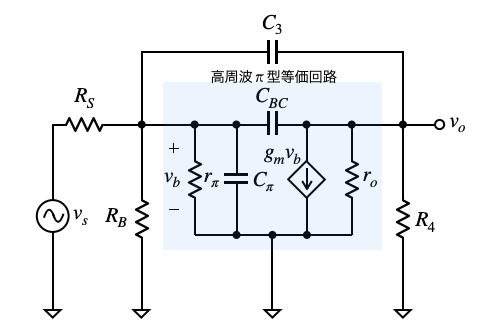
　高周波のコーナ周波数は，Open-Circuit Time Constant法を使って近似値を算出します．Open-Circuit Time Constant法は，図4の電圧源(v_s)をショートにします．そして，複数あるコンデンサの1つを残し，他のコンデンサは，アンプの周波数特性に影響を与えないようにオープンとしたときの時定数を求めます．各々の時定数を加算した後の式に対して逆数をとると，おおよそ全体のコーナ周波数になります．
　図5は，図4のC_πを残し，C₃とC_BCをオープンにした等価回路です．これを使ってC_πに関係する時定数を計算するため，テブナン等価抵抗を求めます．

図5　図4のC_πのみの等価回路
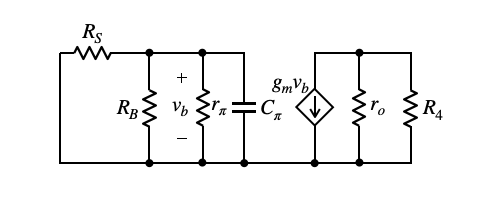
C_πに付くテブナン等価抵抗を求める．

　図5よりC_πに付くテブナン等価抵抗は式11となります．

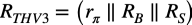・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　図6は，図4のC₃とC_BCの合成した容量を電圧源(v_x)に置き換え，C_πをオープンにした等価回路です．これを使ってC₃とC_BCを合成した容量に関係する時定数を計算するため，テブナン等価抵抗を求めます．

図6　図4のC₃とC_BCを電圧源v_xで表した等価回路
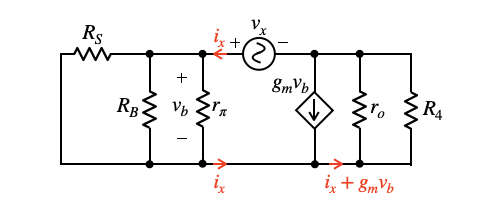
C₃とC_BCに付くテブナン等価抵抗を求める．

　図6よりv_xは，キルヒホッフの電圧則より式12が成り立ちます．

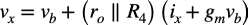・・・・・・・・・・・・・・・・・・・・・・・・・(12)

　式12中のv_bは式13となります．

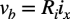・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)

　ここでR_iは，式14の並列抵抗となります．

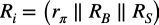・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)

　式12，式13，式14よりv_xは，式15となります．

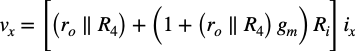・・・・・・・・・・・・・・・・・・(15)

　式15より，v_xに付くテブナン等価抵抗は式16となります．

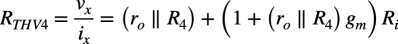・・・・・・・・・・・・・・・(16)

　Open-Circuit Time Constant法を使って計算した，高周波側のトータルのコーナ周波数の近似値は，式17となります．

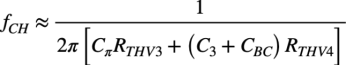・・・・・・・・・・・・・・・・・・(17)

　式17の具体的なコーナ周波数を机上計算します．「r_π=41kΩ」,「R_B=9kΩ」,「R_S=0Ω」,「g_m=7.7mA/V」,「r_o=500kΩ」,「R₄=20kΩ」，2N3904のC_πは「C_π=14.9pF」，C_BCは「C_BC =2.15pF」より，おおよそ「f_CH=82kHz」となります．

●エミッタ接地アンプのシミュレーション
　図1のシミュレーションを実行して周波数特性を確認します．図1には「.measureコマンド」があり，低周波側のコーナ周波数(f_CL)と高周波側のコーナ周波数(f_CH)，またf_CLとf_CH間の帯域幅，中域周波数のゲインを自動測定できます．「.measureコマンド」は次の内容です．OUTの最大ゲインを変数tmpへ入れます．tmpから1/√2 (=-3dB)となる最初の周波数と，最後の周波数のバンド幅をBWへ入れます．

.measure tmp max mag(V(out))
.measure BW trig mag(V(out))=tmp/sqrt(2) rise=1 targ mag(V(out))=tmp/sqrt(2) fall=last

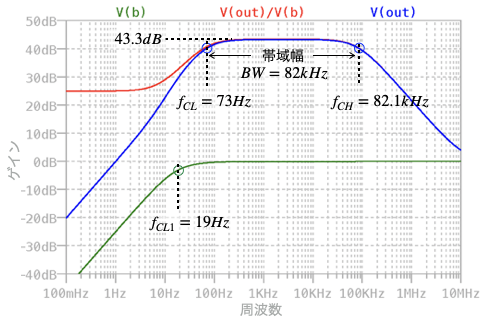
　「.measureコマンド」の結果はログファイル内にあります．図7はシミュレーション終了後に，回路図上で「Ctrl+L」(CtrlキーとLキーを同時押し)で表示させたものです．図7のように低周波と高周波のコーナ周波数，帯域幅，中域周波数のゲインが分かり，机上計算とおおよそ一致しています．

図7　図1の「.measureコマンド」で帯域幅を測った結果

　図8は，C₁を通過した後のBノード周波数特性(緑)，BノードからOUTまでのエミッタ接地アンプの周波数特性(赤)，全体の周波数特性(青)をプロットしました．f_CLより低周波側をみると，緑のプロットはC₁に関係したハイ・パス・フィルタの特性となります．赤のプロットはC₂に関係しており，C₂がオープンとみなせる低周波のときはR₃があるのでゲインは低くなり，C₂がショートとみなせるf_CLとf_CHの間はR₃がショートとなりゲインは高くなります．高周波側のf_CHはC₃によるコーナ周波数となり，更に周波数が高くなるとゲインは低下して0dBに近づきます．このように図1のエミッタ接地アンプはf_CLとf_CH間の帯域幅の交流信号を増幅する回路となります．

図8　図1の周波数特性

　以上解説したように，図1のエミッタ接地アンプはf_CLとf_CH間の周波数の信号を増幅します．シミュレーションでは信号源抵抗のR_Sを0Ωにできますが，実際の回路は信号源抵抗があります．信号源抵抗があると式14のR_iが大きくなり， R_SとC₃のミラー容量により高周波側のコーナ周波数は低くなります．C₁はカップリングコンデンサ，C₂はバイパスコンデンサと呼ばれます．