真のループ・ゲインを求める

■問題
シミュレーション手法 ― 中級

平賀　公久　Kimihisa Hiraga

　図1は，負帰還アンプが発振するか，発振しないかを調べるため，MiddleBrook法を用いたループ・ゲインと位相の周波数特性をプロットした図です．プロット中には各測定点における値を示しています．図1から求められる，位相余裕と利得余裕(a)～(d)のどれでしょうか．

図1　負帰還アンプのループ・ゲインと位相の周波数特性
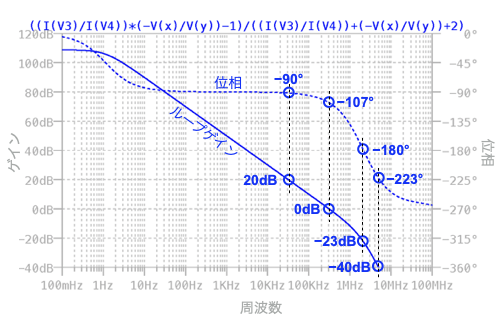
MiddleBrook法を用いてプロットした．

(a) 位相余裕：43°　利得余裕：17dB
(b) 位相余裕：73°　利得余裕：23dB
(c) 位相余裕：90°　利得余裕：20dB
(d) 位相余裕：107° 利得余裕：0dB

■ヒント

　負帰還アンプの発振は，何らかの要因で負帰還ループを一巡したときの振幅と位相が同じになり，正帰還になったときに起こります．位相余裕と利得余裕は，負帰還回路が発振するか，発振しないかを検討するときの目安として用いています．
　位相余裕は，負帰還ループを一巡したときの振幅が同じになったとき，正帰還になるまでの位相差です．
　利得余裕は，一巡したときの位相が同じで正帰還になったとき，同じ振幅になるまでの利得差です．
　MiddleBrook法は一巡するループ・ゲインと位相を調べるときの技法となります．

■解答

(b) 位相余裕：73°　利得余裕：23dB

　図2は，図1の位相余裕と利得余裕を検討した結果です．位相余裕は，負帰還ループを一巡したとき，同じ振幅(ループ・ゲイン=0dB)となるときの位相が正帰還になるまでの位相差を評価します．正帰還になる位相は，ループを一巡したときに-360°(＝0°と同意)のときです．ここで，負帰還ループは，OPアンプの反転端子を通る経路があるので，OPアンプ出力の極性が反転して180°の位相差が発生します．
　これにより，位相余裕は，-360°のうち極性反転の180°を引いた残りの-180°からの位相差となり，図2より「-107°-(-180°)=73°」となります．
　利得余裕は，負帰還ループを一巡したときの位相が-360°の正帰還になったとき，同じ振幅になるまでの利得差を評価します．先ほどと同じように図2で正帰還となる-180°の位相ですので，そのときのループ・ゲインを調べます．図2より同じ振幅になるまでの利得差は「0dB-(-23dB)=23dB」となります．以上より解答は「(b) 位相余裕：73°　利得余裕：23dB」となります．

図2　位相余裕と利得余裕を調べた結果
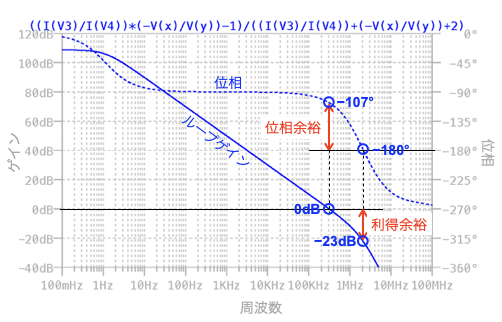
位相余裕が73°，利得余裕が23dBとなる．

■解説

●負帰還アンプの安定性評価について
　図3(a)は，負帰還アンプの回路です．また，図3(b)は，負帰還ループを切り離したループ・ゲインを図示しました．
　図3(a)は，入力信号がIN₁のとき反転アンプ，入力信号がIN₂のとき非反転アンプとなります．このように，負帰還アンプも同じで，信号源の位置によりアンプの特性が変わります．
　負帰還アンプの安定性の評価は，IN₁とIN₂の信号源が無い場合，OUTが発振するか，発振しないかです．なので，反転アンプと非反転アンプとも図3(b)のループ・ゲインが正帰還にどれだけ近づくかを評価をします．

図3　負帰還アンプとループ・ゲインを解説する図
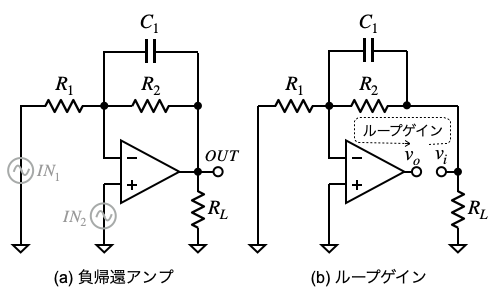
(a) 負帰還アンプの回路図
(b) 負帰還を切り離したときのループ・ゲイン

　ループ・ゲインの評価は，図3(b)のように負帰還ループの一部を切り離す必要があります．しかし，OPアンプは高い直流ゲインがあるので，ループ・ゲインも高くなります．単に配線を切断するとオフセット電圧等の直流誤差が増幅され，OPアンプの出力は，飽和するので評価ができなくなります．
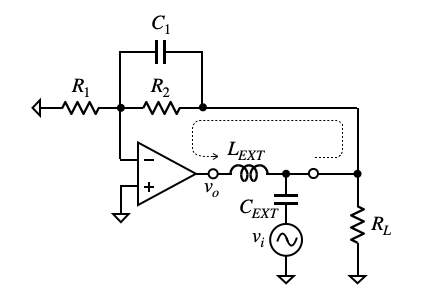
　簡易的に調べる場合，図4のように大きな値のコイル(L_EXT)とコンデンサ(C_EXT)を使ったフィルタ回路を負帰還ループの切り離したいところに入れます．このフィルタは，直流のときコイルがショートし，コンデンサがオープンすると考えると，回路の直流動作点の値は，負帰還のときに落ち着きます．
　逆に，高周波のとき，フィルタは，コイルがオープンで，コンデンサがショートと考えると，v_iの信号が波線で示した経路を一巡したv_oとなり，ループ・ゲインが「v_o/v_i」で計算できます．
　しかし，この方法では，切り離すことで，それ以前のインピーダンスが見えなくなります．なので，おおよそなループ・ゲインの評価はできますが，真のループ・ゲイン評価にはなりません．

図4　ループ・ゲインを調べる簡易法

●電圧注入法と電流注入法を使うMiddleBrook法
　ループ・ゲインと位相を調べる技法として，MiddleBrook法があります．この技法は負帰還ループを切断せずに電圧注入法と電流注入法の2つの回路を用いて，計算により真のループ・ゲインを求める方法です．
　図5は，負帰還アンプの等価回路です．この等価回路を用いてMiddleBrook法を解説します．図5の波線内は，図3(a)のOPアンプの等価回路となり，電圧制御電流源のトランスコンダクタンス(g_m)とOPアンプの出力インピーダンス(z_o)の積がOPアンプのオープン・ループ・ゲインに相当します．z_Lは図3(a)のアンプの出力に接続する負荷(R_L)と負帰還の帰還率(R₁，R₂，C₁)に相当します．

図5　負帰還アンプの等価回路

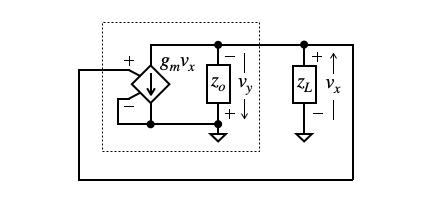
　図5の真のループ・ゲイン(T)を机上計算すると式1になります．

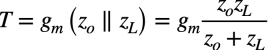・・・・・・・・・・・・・・・・・・・・・・・・(1)

　図6(a)は，図5にv_zの電圧注入した等価回路です．また，図6(b)は，図5にi_zの電流注入した等価回路です．

図6　(a)電圧注入法，(b)電流注入法

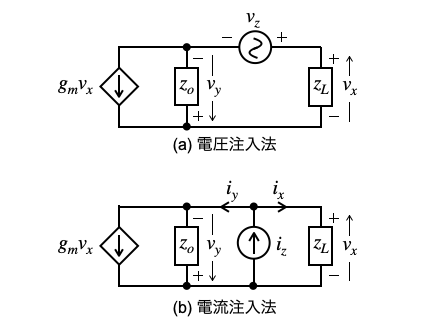
　v_zとi_zは，直流がゼロの交流小信号源とすると直流動作点に影響を与えません．　図6(a)のループ・ゲインは「T_v=v_y/v_x」となり，同様に図6(b)のループ・ゲインは「T_i=i_y/i_x」となります．真のループ・ゲイン(T)はT_vとT_iを使って計算により導きます．この計算については次章で解説します．

●MiddleBrook法を使った真のループ・ゲインの机上計算
　ここでは，真のループ・ゲイン(T)を電圧注入法のループ・ゲイン(T_v)と電流注入法のループ・ゲイン(T_i)で表します．図6(a)のループ・ゲインはキルヒホッフの法則を使って求めると式2となります．

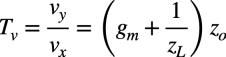・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　式1の真のループ・ゲインより，g_mz_oのゲインは式3となります．

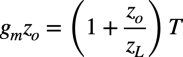・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式2を展開して式3を代入すると，電圧注入法のループ・ゲイン(T_v)は式4となります．式4は「z_o＜＜z_L」の関係のとき「T_v=T」となり，T_vが真のループ・ゲインとなります．

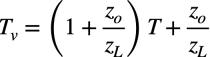・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　次に図6(b)のループ・ゲインは式5となります．

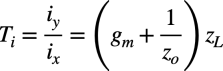・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式1の真のループ・ゲインより，g_mz_Lのゲインは式6となります．

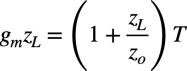・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式5を展開して式6を代入すると，電流注入法のループ・ゲイン(T_i)は式7となります．式7は「z_o＞＞z_L」の関係のとき「T_i=T」となり，T_iが真のループ・ゲインとなります．

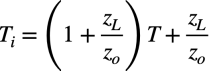・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式4と式7より，真のループ・ゲイン(T)は，電圧注入法の(T_v)と電流注入法の(T_i)で表すと式8になります．

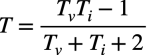・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　以上がMiddleBrook法で，真のループ・ゲイン（T）を電圧注入法のT_vと電流注入法のT_iから求める机上計算となります．この技法を使い，シミュレーションでT_vとT_iに相当するものを調べて，式8へ代入することにより，真のループゲイン（T）が計算で得られます．

●MiddleBrook法のシミュレーション
　図7は，LTspiceのEducationalフォルダにあるMiddleBrook法の回路例です．

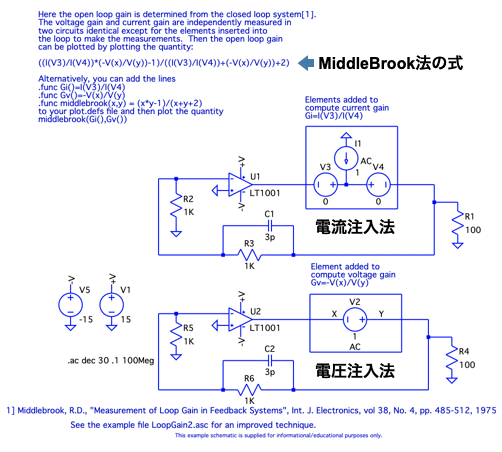
図7　EducationalフォルダにあるMiddleBrook法の回路

　この回路は，図3(a)の負帰還アンプのR₁，R₂，R_L，C₁に具体的な値を入れた回路となります．図6と図7を比べると，電圧注入法と電流注入法の関係は次のようになります．

i_z　→　I1
i_x　→　V4に流れる電流
i_y　→　V3に流れる電流
v_z　→　V2
v_x　→　Yの電圧
v_y　→　-Xの電圧

　シミュレーションを実行後，「T_i= I(V3)/I(V4)」,「T_v=-V(x)/V(y)」とし，それらを式8へ入れた計算式「((I(V3)/I(V4))*(-V(x)/V(y))-1)/((I(V3)/I(V4))+(-V(x)/V(y))+2)」をプロットすれば，LTspiceを使ったMiddlebrook法のループ・ゲインのシミュレーション結果となります．
　図7をシミュレーションした結果が図1となります．このプロットから位相余裕と利得余裕を検討したのが解答「(b) 位相余裕：73°　利得余裕：23dB」になります．

　以上，解説したように負帰還アンプのループ・ゲインと位相のシミュレーションは，負帰還ループを切り離さなくてもMiddleBrook法で真のループ・ゲインを求めることができます．負帰還ループへ電圧注入法と電流注入法の加え方が分かれば他の負帰還アンプにも応用できると思います．実際の回路設計では図2の位相余裕と利得余裕を目安にして調整し，過渡解析で発振の有無を確認します．