ひずみが少ない正弦波発振回路

■問題
発振回路 ― 中級

平賀　公久　Kimihisa Hiraga

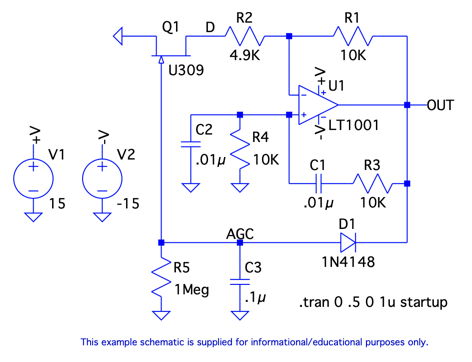
　図1は，AGC(Auto Gain Control)付きのウィーン・ブリッジ発振回路です．この回路は発振が成長して落ち着くと，正側と負側の発振振幅が一定になります．そこで，発振振幅が一定を表す式は，次の(a)～(d)のうちどれでしょうか．

図1　AGC付きウィーン・ブリッジ発振回路 Q₁はNチャネルJFET.

(a) ±(V_GS-V_D1)
(b) ±V_D1
(c) ±(1+R₂/R₁)V_D1
(d) ±(1+R₂/(R₁+R_DS))V_D1
ここで，V_GS：Q₁のゲート・ソース電圧，V_D1：D₁の順方向電圧，R_DS：Q₁のドレイン・ソース間の抵抗

■ヒント

　図1のD₁は，OUTの電圧が負になったときダイオードがONとなるスイッチです．D₁がONのときのOUTの電圧を検討すると分かります．

■解答

(a) ±(V_GS-V_D1)

　図1は，LTspice EducationalフォルダにあるAGC付きウィーン・ブリッジ発振回路です．この発振回路は，Q₁のゲート・ソース電圧によりドレイン・ソース間の抵抗が変化して発振を成長させたり抑制したりします．また，AGCにより，Q₁のゲート・ソース電圧をコントロールして発振を継続するために適したゲインへ自動調整します．発振が落ち着いたときのQ₁のゲート・ソース電圧は，コンデンサ(C₃)で保持され，ドレイン・ソース間の抵抗は一定になります．
　負側の発振振幅の最大値は，ダイオード(D₁)がONしたときで，Q₁のゲート・ソース間電圧からD₁の順方向電圧を減じた「V_GS-V_D1」となります．正側の発振振幅の最大値は，D₁がOFFのときです．しかし，C₃によりQ₁のゲート・ソース間は保持され，発振を継続するために適したゲインと最大振幅の条件を保っています．この動作により正側の発振振幅の最大値は負側の最大値の極性が変わった「-(V_GS-V_D1)」となります．以上より，発振が落ち着いたときの振幅は，(a) ±(V_GS-V_D1)となります．

■解説

●ウィーン・ブリッジ発振回路について
　図2は，ウィーン・ブリッジ発振回路の原理図を示します．ウィーン・ブリッジ発振回路は，コンデンサ(C)と抵抗(R)からなるバンド・パス・フィルタ(BPF)とG倍のゲインを持つアンプで正帰還ループを構成した発振回路となります．

図2　ウィーン・ブリッジ発振回路の原理

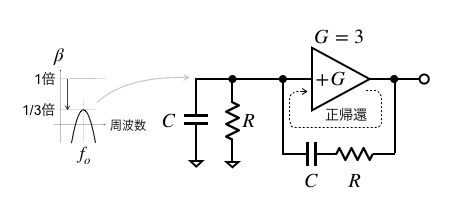
　CとRによる帰還率(β)は，式1のBPFの中心周波数(fo)でゲインが1/3倍になります．

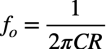・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　正帰還の発振を継続させるための条件は，ループ・ゲインが「Gβ=1」です．なので，アンプのゲインは「G=3」に設定します．図1ではQ₁のドレイン・ソース間の抵抗(R_DS)を約100ΩになるようにAGCが動作し，OPアンプ(U₁)やR₁，R₂，R_DSからなる非反転アンプのゲインが「G=1+R₁/(R₂+R_DS)=3」になるように動作しています．発振周波数や帰還率の詳しい計算は「LTspiceアナログ電子回路入門 ―― ウィーン・ブリッジ発振回路が適切に発振する抵抗値はいくら？」を参照してください．

●AGC付きウィーン・ブリッジ発振回路のシミュレーション
　図3は，図1を過渡解析でシミュレーションした結果です．図3は時間0sからのOUTの発振波形の推移，Q₁のV_GSの推移(AGCラベルの電圧)，Q₁のドレイン電圧をドレイン電流で除算したドレイン・ソース間の抵抗(R_DS)の推移をプロットしました．

図3　図2のシミュレーション結果

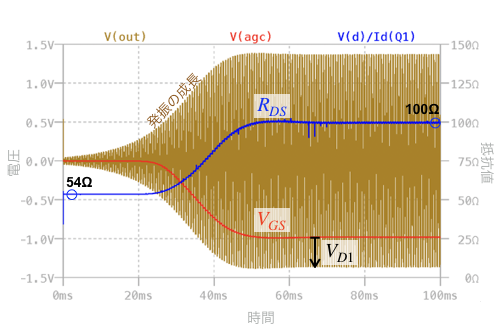
　図3の0s～20ms付近までQ₁のV_GSは，0Vです．Q₁は，NチャネルJFETなので「V_GS=0V」のときONとなり，ドレイン・ソース間の抵抗が「R_DS=54Ω」となります．このとき，回路のゲインは「G=1+R₁/(R₂+R_DS)=3.02」となり，発振条件のループ・ゲインが1より大きい「Gβ>1」となるため発振が成長します．　発振が成長するとD₁がONし，V_GSはC₃とR₅で積分した負の電圧になります．V_GSが負の電圧になるとNチャネルJFETに流れる電流が小さくなりR_DSが大きくなります．この動作により回路のゲインが「G=3」になる「R_DS=100Ω」の条件に落ち着き，負側の発振振幅の最大値は「V_GS-V_D1」となります．正側の発振振幅のときD₁はOFFとなり，C₃によりQ₁のゲート・ソース間は保持されて発振を継続するために適したゲインと最大振幅の条件を保ちます．このため正側の発振振幅の最大値は「-(V_GS-V_D1)」となります．
　図4は，図3の時間軸を498ms～500ms間の拡大したプロットです．

図4　図3の時間軸を拡大(498ms?500ms間)

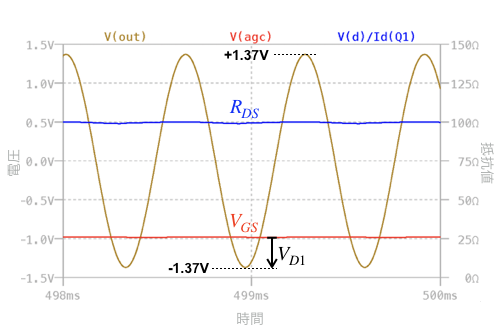
　図4は，時間軸を拡大したプロットのため，OUTの発振波形が正弦波になっています．負側の発振振幅の最大値は，約「V_GS=-1V」からD₁がONする順方向電圧「V_D1=0.37V」だけ下がった電圧となります．正側の最大振幅は，負側の電圧の極性が変わった値なので，発振振幅が「±(V_GS-V_D1)=±1.37V」となります．
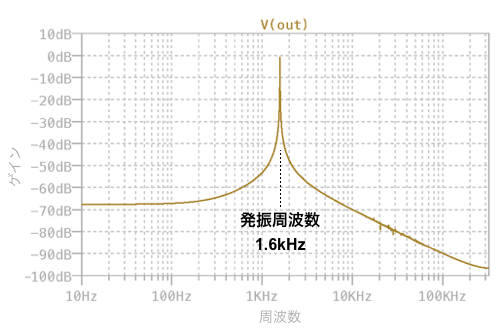
　図5は，図3のOUTの発振波形をFFTした結果です．発振周波数は式1の「R=10kΩ，C=0.01μF」としたときの周波数「f_o=1.6kHz」となり，高調波ひずみが少ない正弦波の発振であることが分かります．

図5　図3のFFT結果(400ms～500ms間)

●AGCにコンデンサやJFETを使わない回路
　図1のAGCは，コンデンサやNチャネルJFETが必要でした．しかし，図6のようにダイオード(D₁とD₂)のON/OFFを使って回路のゲインを「G=3」に自動で調整するウィーン・ブリッジ発振回路も使われています．ここでは，この回路のゲイン設定と発振振幅について検討します．

図6　AGCにコンデンサやJFETを使わない回路

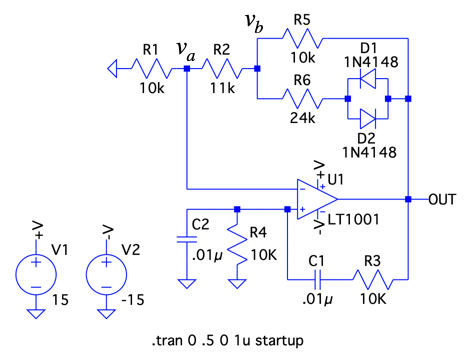
　図6の回路でD₁とD₂がOFFとなる小さな発振振幅のときは，発振を成長させるために回路のゲインを「G₁>3」にします．これより式2の条件が成り立ちます．図6では回路の抵抗値より「G₁=3.1」に設定しました．

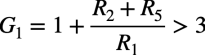・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　発振が成長してD₁とD₂がONするOUTの電圧になると，発振振幅を抑制するために回路のゲインを「G₂<3」にします．D₁とD₂のオン抵抗を0Ωと仮定して計算を簡単にすると式3の条件となります．　図6では回路の抵抗値より「G₂=2.8」に設定しました．

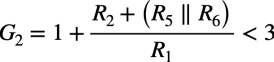・・・・・・・・・・・・・・・・・・・・・・・・(3)

　次に発振振幅について検討します．発振を継続させるには「G=3」の条件なので，OPアンプの反転端子の電圧をv_aとすると，発振振幅v_outとの関係は式4となります．

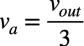・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　また，R₂とR₅の接続点の電圧をvbとすると，その電圧はv_aにR₂の電圧効果を加えた電圧なので，式5となります．

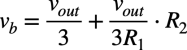・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　発振が落ち着いているとき，R₁の電流は，R₅とR₆の電流を加えた値なので式6となります．

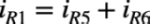・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　i_R1，i_R5，i_R6の各電流を式4と式5の電圧と回路の抵抗からオームの法則で求め，式6へ代入して整理すると発振振幅は式7となります．ここでV_DはD₁とD₂がONしたときの順方向電圧です．

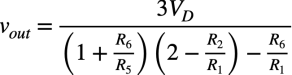・・・・・・・・・・・・・・・・・・・・・・・(7)

　図6のダイオードと図1のダイオードは，同じダイオードなので，順方向電圧を図4から求まる「V_D=0.37V」とし，回路の抵抗値を用いて式7の発振振幅を求めると「±1.64V」と概算できます．

●AGCにコンデンサやJFETを使わない回路のシミュレーション
　図7は，図6のシミュレーション結果で，OUTの電圧をプロットしました．OUTの発振振幅は正弦波の発振で出力振幅は「±1.87V」となり，式7を使った概算に近い出力電圧となります．　実際の回路では，R₂の構成に可変抵抗を加えた抵抗とし，発振振幅を調整すると良いと思います．

図7　図6のシミュレーション結果
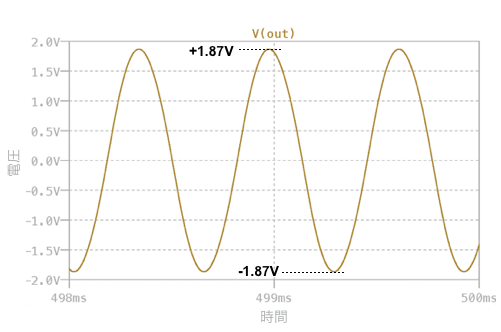
発振振幅は±1.87V．

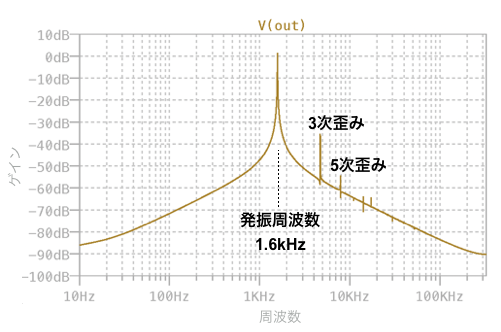
　図8は，図7のOUTの発振波形をFFTした結果です．発振周波数は式1の「R=10kΩ，C=0.01μF」としたときの周波数「f_o=1.6kHz」となります．図5の結果と比べると3次高調波や5次高調波のクロスオーバひずみがありますが，図1のコンデンサとNチャネルJFETを使わなくても実用的な正弦波発振回路となります．