ハイ/ロー/バンドパスとして働くフィルタ

■問題
フィルタ回路 ― 中級

小川　敦　Atsushi Ogawa

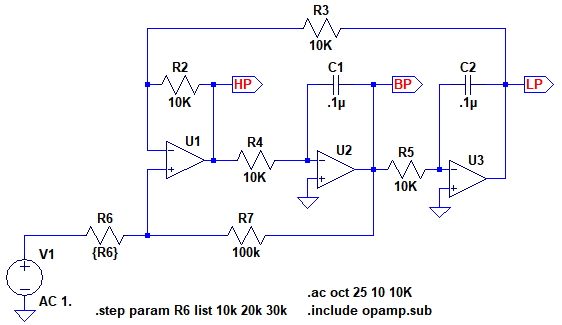
　図1は，OPアンプを使用したステート・バリアブル・フィルタ(State Variable Filter)をシミュレーションするための回路です．ステート・バリアブル・フィルタは，出力を取り出す場所によって，ハイパス・フィルタ(HP端子)，ローパス・フィルタ(LP端子)，バンドパス・フィルタ(BP端子)の3種類のフィルタとして働きます．
　図1の回路でR₆の抵抗値を10kΩ，20kΩ，30kΩと変化させたときの特性変化の説明として正しいのは(a)～(d)のどれでしょうか．

図1　OPアンプを使用したステート・バリアブル・フィルタ
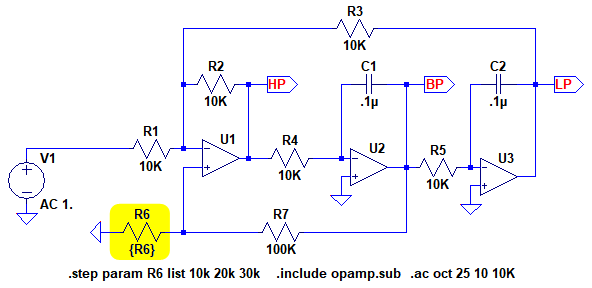
R₆の抵抗値を変化させたときの特性変化の説明として正しいのどれ？

(a) ハイパス・フィルタの通過帯域全体のゲインが変化する
(b) ローパス・フィルタの通過帯域全体のゲインが変化する
(c) バンドパス・フィルタの通過帯域のゲインが変化する
(d) 3種類のフィルタとも，通過帯域のゲインは変化しない

■ヒント

　ステート・バリアブル・フィルタ(State Variable Filter)は，状態変数フィルタとも呼ばれ，2つの積分器と加算器で構成されています．そして，カットオフ周波数とQ（選択度）を独立して設定できるという特長があります．図1の回路は，反転入力型のステート・バリアブル・フィルタとなっています．R₆の抵抗値を変えることでQを変えることができます．そこで，Qが変わったときに，どのような特性となるかを考えれば，答えが分かります．

■解答

(c) バンドパス・フィルタの通過帯域のゲインが変化する

　図1の回路のQ（選択度）は，R₆とR₇で決まり，Q=(R₆+R₇)/(3R₆)となります．そしてバンドパス・フィルタ出力の通過帯域のゲイン(G_B)はG_B=R₇/R₆で表されます．そのため，R₆の値が変わるとゲインが変化します．なお，ハイパス・フィルタ出力とローパス・フィルタ出力の通過帯域のゲインはR₁～R₃で決まり，図1の定数では1になります．そのため，Qを変化させたときに変化するのは，カットオフ周波数付近のゲインだけです．

■解説

●ステート・バリアブル・フィルタのカットオフ周波数とQ
　図1のステート・バリアブル・フィルタは，OPアンプU2とR₄およびC₁で積分回路をを構成しています．同様に，OPアンプU3とR₅およびC₂も積分回路を構成しています．それぞれの積分時定数が等しくなるように「R₄=R₅=R」とし，「C₁=C₂=C」とします．また，「R₁=R₂=R₃」とすると，カットオフ周波数（バンドパス・フィルタの中心周波数）は式1で表されます．

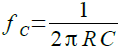・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　式1に値を代入すると式2のようにカットオフ周波数は，159Hzとなります．

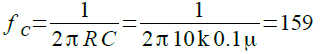・・・・・・・・・・・・・・・・・・・・・(2)

　ハイパス・フィルタの通過帯域のゲイン(G_H)は，式3で表され，G_Hが1倍となります．

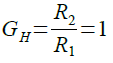・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　ローパス・フィルタの通過帯域のゲイン(G_L)は，式4で表され，G_Lが1倍となります．

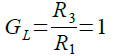・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　Qは，式5で表されます．また，バンドパス・フィルタの通過帯域のゲイン(G_B)は式6で表されます．QとG_Bは同じ式で表されます．

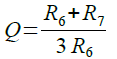・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

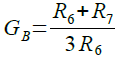・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　ですので，図1でR₆の値が10kΩのときの値を計算すると，バンドパス・フィルタのQとゲイン(G_B)は式7のように3.67となります．

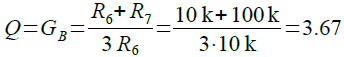・・・・・・・・・・・・・・・・・・・(7)

●ステート・バリアブル・フィルタのシミュレーション
　図2は，図1のステート・バリアブル・フィルタのシミュレーション結果です．

図2　図1のステート・バリアブル・フィルタのシミュレーション結果
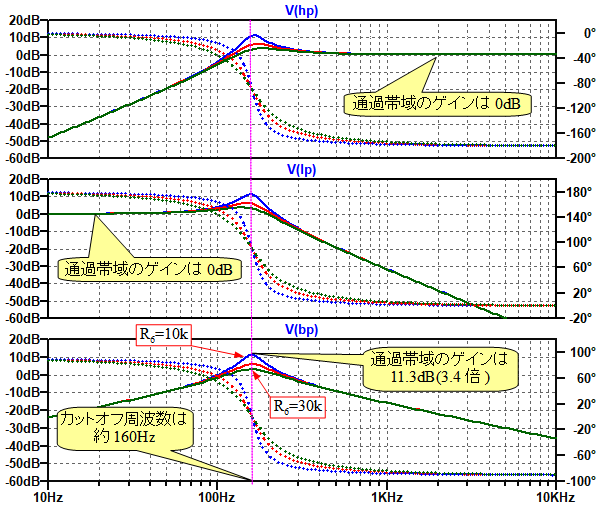
R₆の値を変えることで，各フィルターのQが変化していることが分かる．

　R₆の値を「.stepコマンド」で10kΩ，20kΩ，30kΩと変えてシミュレーションしています．R₆の値を変えることで，各フィルターのQが変化しています．また，ハイパス・フィルタ(HP)およびローパス・フィルタ(LP)の通過帯域内のゲインは1で，Qを変えても変わらないことが分かります．
　バンドパス・フィルタ(BP)のゲインはR₆が10kΩのとき，11.3dB(3.4倍)となっており，式7の結果と一致しています．また各フィルタのカットオフ周波数は約160Hzとなっており，これも式2と一致しています．

●非反転入力型のステート・バリアブル・フィルタ
　図3は，信号の入力をOPアンプの非反転入力側に変えた，ステート・バリアブル・フィルタです．

図3　非反転入力型のステート・バリアブル・フィルタ
信号の入力がOPアンプの非反転入力側になっている．

　この回路でも「R₄=R₅=R」，「C₁=C₂=C」として，「R₂=R₃」とすると，カットオフ周波数は図1と同様に式1で表されます．そして，Qは式8に変わります．

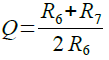・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　また，ハイパス・フィルタの通過帯域のゲイン(G_H)とローパス・フィルタの通過帯域のゲイン(G_L)は式9となります．

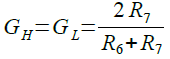・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)

　G_HとG_LがR₆とR₇で決まるため，Qを変えるためにR₆，R₇の値を変えるとG_HとG_Lも変わることになります．さらにバンドパス・フィルタの通過帯域のゲイン(G_B)は式10で表されます．

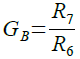・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　図4が非反転入力タイプのステート・バリアブル・フィルタのシミュレーション結果です．

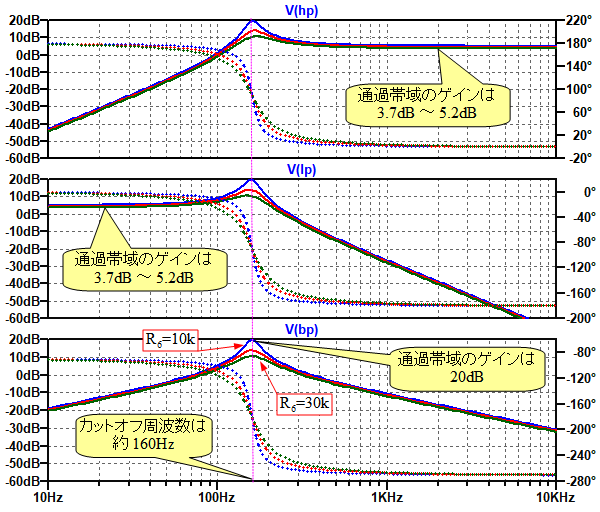
図4　非反転入力タイプのステート・バリアブル・フィルタのシミュレーション結果
Qを変えることで，ハイパス・フィルタとローパス・フィルタのゲインも若干変化する．

　図1と同様にR₆の値を「.stepコマンド」で10kΩ，20kΩ，30kΩと変えてシミュレーションしています．カットオフ周波数は図1の回路のシミュレーション結果と同じで，約160Hzになっています．R₆を変えることでQが変化していますが，ハイパス・フィルタ(HP)およびローパス・フィルタ(LP)の通過帯域内のゲインも若干変化しています．
　そのため，ハイパス・フィルタとローパス・フィルタとして使用する場合は，通過帯域のゲインが変わらない，反転入力型のステート・バリアブル・フィルタのほうが，適しています．また，バンドパス・フィルタとして使用する場合は，図3の非反転入力タイプのステート・バリアブル・フィルタのほうが，抵抗が1本少なくて済むというメリットがあります．
　以上，ステート・バリアブル・フィルタについて解説しました．なお，図1はLTspiceのサンプルファイル(ドキュメント\LTspiceXVII\examples\Educational\opamp.asc)を若干変更したものです．ステート・バリアブル・フィルタの伝達関数等に関しては，「IoT時代のLTspiceアナログ回路入門アーカイブs ―― 3つの機能を有するフィルタの特性」を参考にしてください．