全波整流回路の動作

『LTspice Users Club』のWebサイトはこちら

■問題
オペアンプ応用 ― 初級

平賀　公久　Kimihisa Hiraga

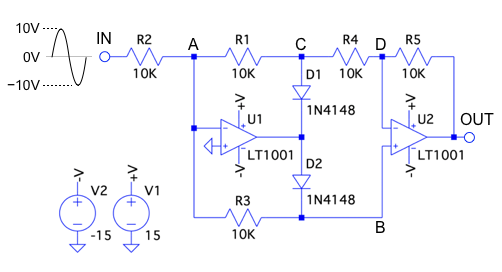
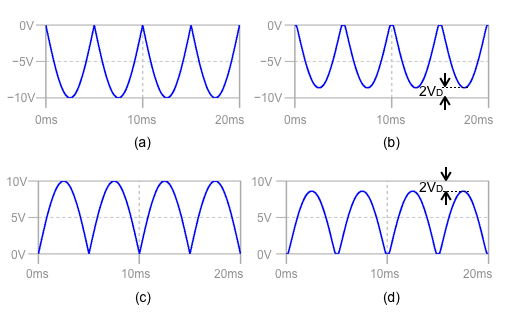
　図1は，OPアンプを使った全波整流回路です．IN端子へ振幅が10Vの正弦波を入力します．このときのOUT端子の波形として正しいのは図2の(a)～(d)のうちどれでしょうか．

図1　OPアンプを使った全波整流回路
振幅が10Vの正弦波を入力している．

図2　OUT端子の電圧波形
(b)と(d)の2VDはダイオードの順方向電圧が2個分の電圧．

(a)の波形　(b)の波形　(c)の波形　(d)の波形

■ヒント

　全波整流回路は，AC信号からDC信号への生成に使われ，信号のピーク電圧や平均電圧等を作るときに用いられます．全波整流回路は，入力電圧が正の電圧と負の電圧でダイオードD₁とD₂のON/OFFの状態が変わり，回路の接続が変化します．接続が変化した2つの回路において，出力電圧がどのようになるかを検討すると分かります．図2の(a)と(b)は負側に信号が現れる全波整流波形で振幅に差があります．(c)と(d)は正側に信号が現れる全波整流波形で振幅に差があります．

■解答

(c)の波形

　入力電圧が正のとき，D₁がON，D₂がOFFとなります．このとき，IN端子からCノードまではR₁，R₂，U₁からなる反転アンプとなります．図1の抵抗は全て10kΩなので，ゲインは「G₁=-1」となります．同様にCノードからOUT端子まではR₄，R₅，U₂からなる反転アンプとなり，ゲインは「G₂=-1」となります．IN端子からOUT端子までのトータルゲインは「G₁G₂=1」となり「V_OUT=V_IN」となります．
　入力電圧が負のときはD₁がOFF，D₂がONとなります．回路図中のAのノードはバーチャル・グラウンド，　BノードとCノードはバーチャル・ショートとなり，この2つの効果でIN端子からBノードまでのゲインは「G₃=-2/3」となります．またBノードからOUT端子まではR₁，R₄，R₅，U₂からなる非反転アンプとなり，ゲインは「G₄=3/2」となります．IN端子からOUT端子までのトータルゲインは「G₃G₄=-1」となり「V_OUT=-V_IN」となります．以上より，入力電圧が正のときは「V_OUT=V_IN」，入力電圧が負のときは「V_OUT=-V_IN」なので，OUT端子の波形は振幅が10Vの正側に信号が現れる全波整流回路となり，答えは図2(c)となります．

■解説

●入力信号が正のときの動作解説
　図1は，R₁，R₂，R₃，R₄，R₅が10kΩと同じ抵抗値で構成できる高精度な全波整流回路です．入力信号が正の電圧と負の電圧でD₁とD₂のON/OFFが切り替わって回路が変化します．ここでは，切り替わる回路図を用いて動作解説をします．
　図3は，入力信号が正（V_IN>0）の等価回路です．IN端子の信号は，OPアンプU₁の反転端子に繋がるため，IN端子が正のときはU₁の出力は負となります．これよりCノードからU₁出力の方向に電流が流れる回路となり，D₁がONとなります．図1のD₂あたるダイードはOFFとなので図3にはありません．

図3　入力電圧が正のときの回路
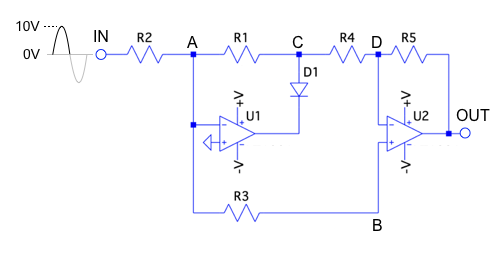
D₁がON．図1のD₂あたるダイードはOFFとなので図3にはありません．

　図3のD₁がONなので，R₁，R₂，U₁は，IN端子が入力でCノードが出力の反転アンプとして動作します．「R₁=R₂」なので，ゲインは-1倍となります．次にAノードはU₁の負帰還によりバーチャル・グラウンドです．OPアンプの入力端子には電流が流れないとすればR₃による電圧降下は無いためBノードもグラウンドと考えることができます．よってR₄，R₅，U₂はCノードが入力でOUT端子が出力の反転アンプとなります．「R₄=R₅」なので，ゲインは-1倍となります．以上よりIN端子からOUT端子までは反転アンプを2回路通過するのでトータルゲインは1倍となり式1の関係となります．式1より入力信号が正のときは，入力と同じ波形がOUT端子に現れます．

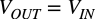・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

●入力信号が負のときの動作解説
　図4は，入力信号が負（V_IN＜0）のときの等価回路です．IN端子が負のときはU₁の出力は正となります．これよりU₁出力からBノードの方向に電流が流れる回路となり，D₂がONとなります．図1のD₁あたるダイードはOFFとなので図4にはありません．

図4　入力電圧が負のときの回路
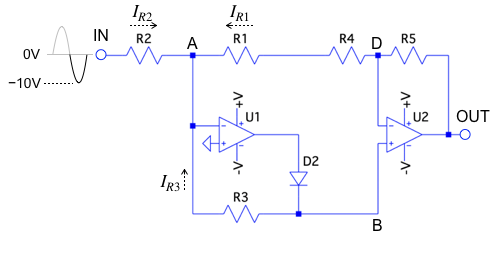
D₂はON．図1のD₁あたるダイードはOFFとなので図4にはありません．

　図4のAノードは，U₁の負帰還によりバーチャル・グラウンドです．また，BノードとDノードは，U₂の負帰還によりバーチャル・ショートとなり同じ電圧になります．これらを使ってIN端子からB端子までの関係を調べます．キルヒホッフの電流則よりA端子に流れ込む電流の総和はゼロであり「I_R1+I_R2+I_R3=0」となります．図4の抵抗値は全て同じ「R₁=R₂=R₃=R₄=R₅＝R」とし，Bノードの電圧をV_Bとすれば，「I_R1=V_B/2R」，「I_R2=V_IN/R」，「I_R3=V_B/R」の関係があります．これらよりIN端子の電圧とBノードの電圧は式2の関係となります．

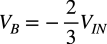・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　次にA端子は，バーチャル・グランドなので，BノードからOUT端子まではR₁，R₄，R₅，U₂からなる非反転アンプとなり式3となります．

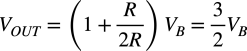・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式2と式3よりIN端子からOUT端子までのトータルゲインは-1倍となり式4の関係となります．

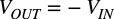・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式4より入力信号が負のときは，負側の振幅が反転してOUT端子に現れます．以上より，入力信号が正（V_IN>0）のときは式1，入力信号が負（V_IN＜0）のときは式4となり，正側に波形が現れる全波整流回路であることが分かります．過去の「LTspiceアナログ電子回路入門 ―― 全波整流になる抵抗の組み合わせはどれ？」で全波整流回路について詳細な解説をしています．こちらも参考にしてください．

●全波整流回路のシミュレーション
　図5は，LTspiceのjigsフォルダにある全波整流回路「1001.asc」です．OPアンプが「LT1001」，スイッチング・ダイオードが「1N4148」，抵抗はR₁，R₂，R₃，R₄，R₅全て10kΩで構成しています．入力は振幅が10V，周波数が100Hzの正弦波です．この回路を20msまで過渡解析をおこないます．

図5　図1をシミュレーションする回路

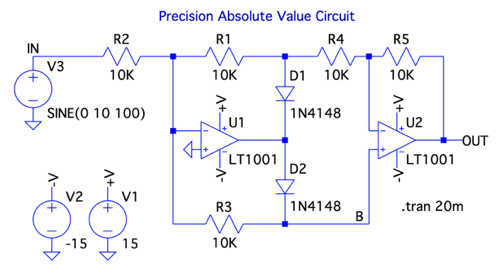
　図6は，図5のシミュレーション結果です．上段が入力の波形，中段がBノードの波形，下段がOUT端子の波形です．入力信号は，正（V_IN>0）のとき，式1ですから，正側の半坡がOUT端子に現れます．入力信号が負（V_IN＜0）のとき，Bノードは式2の関係になっていることが分かります．これを式3の非反転アンプで増幅するため，OUT端子の波形は式4のように負側の半坡が正側に現れます．OUT端子の波形は図2(c)と同じであることが分かります．

図6　図5のシミュレーション結果
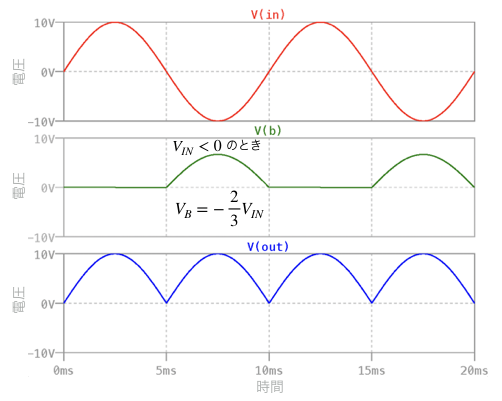
上段が入力電圧波形，中段がBの電圧波形，下段がOUTの電圧波形．

●全波整流の平均値
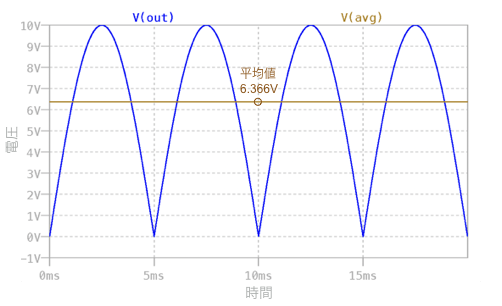
　図7は，図5のOUT端子へR₆とC₁からなる積分回路を追加して，全波整流から平均値を取り出す回路です．入力は振幅が10V，周波数が100Hzの正弦波で，積分回路が落ち着く29.98秒～30秒の間をシミュレーションします．

図7　図1の出力にR₆とC₁からなる積分回路を追加した回路

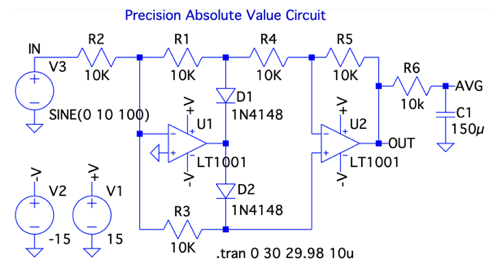
　図8は，図7のシミュレーション結果です．全波整流の平均値は振幅をV_mとすると式5となります．振幅は「V_m=10V」ですから，式5の平均値は「V_AVG=6.366V」と机上計算できます．図8の結果より平均値をカーソルで調べると机上計算と同じ6.366Vの結果となります．

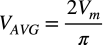・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)