ジャイレータの特性と理想トランス

図1は,ジャイレータ(波線部分)を解説する回路です.ジャイレータに電圧源(V)と負荷(Z)を接続しています.そこで,負荷(Z)に「抵抗(R)」,「コンデンサ(C)」,「コイル(L)」,「直流電圧源」を接続した場合,電圧源側から見た入力インピーダンスについて(a)~(d)で間違えているものはどれでしょうか.
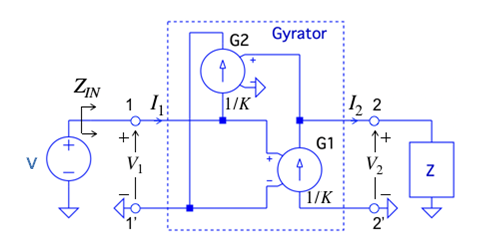
電圧源側から見た入力インピーダンスはどうなるでしょうか.
(a)抵抗(R)を接続すると1/Rの関係が見える
(b)コンデンサ(C)を接続するとコイル(L)に見える
(c)コイル(L)を接続するとコンデンサ(C)に見える
(d)直流電圧源を接続すると0Ωに見える

ジャイレータは,インピーダンスを変換する回路です.式1のように電流を電圧に変換します.
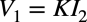 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また,式2のように電圧を電流に変換します.ここでKは定数です.
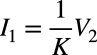 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
この作用で,ジャイレータは電圧源から見た負荷の入力インピーダンスが変化する面白い特徴を持っています.また,ジャイレータの電圧源側に流れる電流は,負荷側の電圧に依存し(電圧依存電流源G2)します.また,反対の負荷側の電流は,電圧源側の電圧に依存(電圧依存電流源G1)するため式1と式2の関係があります.この2つの式と負荷(Z)の電流と電圧で,入力インピーダンスを表す「ZIN=V1/I1」が簡単に求まります.負荷(Z)が,抵抗,コンデンサ,コイル,電源のときの入力インピーダンスを検討すると分かります.
まず,負荷(Z)が付いたときの電圧(V2)と電流(I2)の関係を調べると式3となります.
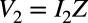 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
入力インピーダンスは式1を式2で割り,式3の関係を入れると式4となります.
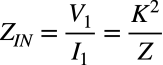 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4で,Zは分母にありますので,抵抗,コンデンサ,コイルのときは,電圧源側の入力インピーダンスは,負荷側の負荷の逆回路となります.具体的には,抵抗(Z=R)がつくと式4は式5となり,「(a)抵抗(R)を接続すると1/Rの関係が見える」は正しいです.
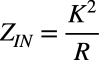 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
コンデンサ(Z=1/jωC)がつくと,式4は式6に示すコイルのインピーダンスを表す式となり,「(b)コンデンサ(C)を接続するとコイル(L)に見える」は正しいです.
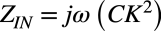 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
コイル(Z=jωL)がつくと,式4は式7に示すコンデンサのインピーダンスを表す式となり,「(c)コイル(L)を接続するとコンデンサ(C)に見える」は正しいです.
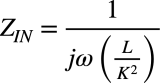 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
直流電圧源(V2=DC電圧)がつくと,V1が変動してもI1は一定となり電流の変化はありません.したがって入力インピーダンスは無限大となります.そこで「(d)直流電圧源を接続すると0Ωに見える」が間違いとなります.よって,解答は(d)となります.
●ジャイレータについて
ジャイレータへ負荷をつけたときの入力インピーダンスは式5,式6,式7の効果があります.式6の「CはK2倍した大きなコイルになる」はフィルタ回路で使われています.大きなコイルを作るときは巻線が多くなり直列抵抗も大きくなりますが,ジャイレータを使い,精度のよい小さなコンデンサで直列抵抗が小さいK2倍した大きなコイルができれば回路の性能は良くなります.また,後で解説する理想トランスもジャイレータの縦続接続で作ることができます.
ここでは,ジャイレータの2ポートの電圧と電流の関係を表す伝送行列と,その記号について解説します.ジャイレータの電圧源側と負荷側の電圧と電流の関係は式1と式2であり,伝送行列(F行列)を使って表すと式8となります.
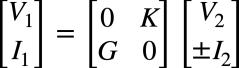 ・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
ここでI2の符号は,ジャイレータから流れ出る電流の方向がプラスで,流れ込む電流の方向がマイナスです.Kは,ジャイレッション抵抗と呼び,「G=1/K」をジャイレッション・コンダクタンスと呼びます.
図1の波線で囲った2ポートのジャイレータは,図2の回路記号を用います.

Kをジャイレッション抵抗と呼ぶ
●大きな等価コイルをシミュレーションで確かめる
図3(a)は,図1の回路をシミュレーションする回路です.図3(b)は,図3(a)のコイルの周波数特性と比較するための通常のコイルの回路です.
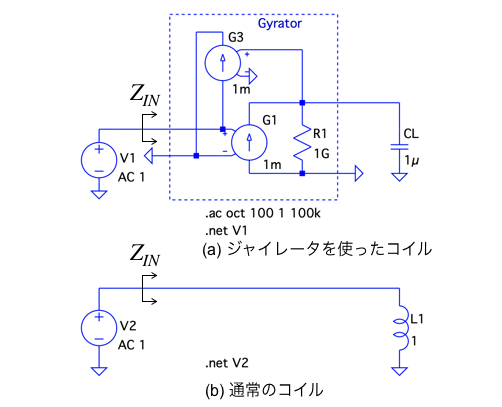
図3(a)の負荷(Z)へコンデンサ(C)を接続して,入力インピーダンスが大きなコイルになる例です.図3(a)のジャイレータは,R1が無いとG1の電流源からGNDに対しての経路がなくエラーとなるため,絶縁抵抗の意味で大きな抵抗値の1GΩを入れています.
図3(b)は,式6を使ったコイルの値を入れています.具体的には,図3(a)で「CL=1μF」,G1とG3のジャイレッション・コンダクタンスを「G=1mA/V」とすると,コイルの値は「L1=1H」となります.
図4は,図3で「.net」コマンドを使った,ネットワーク・パラメータのシミュレーション結果です.上段が図3(a)のV1側から回路を見た入力インピーダンスの値と位相です.下段が図3(b)のV2側からコイルを見た入力インピーダンスの値と位相の結果です.上段と下段の特性は同じであり,図3(a)の1μFの容量は入力側からみると1Hの大きなコイルと等価になることが分かります.
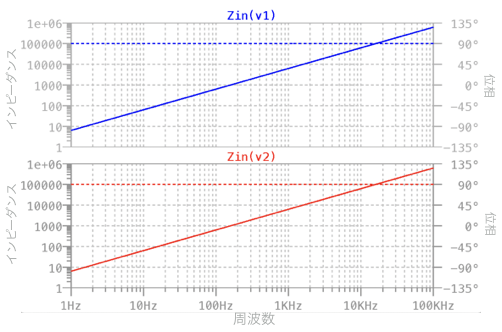
上段と下段のシミュレーション結果は等しい.
●トランスの伝送行列について
ここでは,図5のトランスの伝送行列について調べます.調べた伝送行列は,次に解説する理想トランスと比較します.
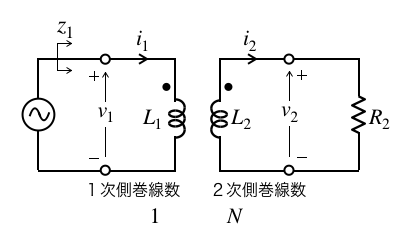
図5のトランスで,負荷側の巻線は電圧源側の巻線のN倍とすると,電圧源側の電圧と負荷側の電圧は式9の関係となります.
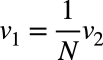 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
同様に,電圧源側の電流と負荷側の電流の関係は式10となります.
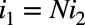 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
式9と式10で,図5のトランスは伝送行列を使って表すと式11となります.
 ・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・(11)
トランスの電圧源から見たインピーダンス(z1)は,式9を式10で割り,R2の電圧と電流の関係から式12となります.
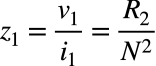 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
●ジャイレータを使って理想トランスを作る
図6は,2つのジャイレータを縦続接続した回路です.ジャイレータの特徴としてこのように接続すると理想トランスとなります.
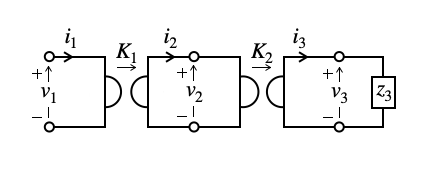
以下では図6の理想トランスを伝送行列で表し,式11と比べます.図6の左側のジャイレータは式13となります.
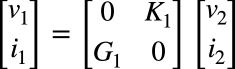 ・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
同様に,右側のジャイレータは式14となります.
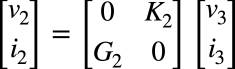 ・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
式13へ式14を代入すると式15となります.
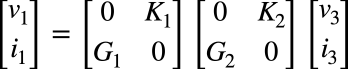 ・・・・・・・・・・・・・・・・・・(15)
・・・・・・・・・・・・・・・・・・(15)
式15を整理すると式16となります.
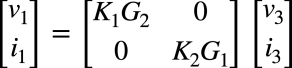 ・・・・・・・・・・・・・・・・・・・・・・(16)
・・・・・・・・・・・・・・・・・・・・・・(16)
式16の伝送行列で,「K1=1」,「G1=1」,「K2=N」,「G2=1/N」とすれば,図5のトランスを使って調べた式11と同じになり,図6は理想トランスとして機能することが分かります.
●理想トランスのシミュレーション
図7(a)はLTspiceのEducationalフォルダにある理想トランスの回路「IdealTransformer.asc」です.比較のため,図7(b)はトランスの記号で表した回路を追加しました.理想トランスはジャイレータを図6のように接続すれば良いので,図1の波線で囲ったジャイレータを縦続接続しています.R2はG1とG2の電流源からGNDヘの電流経路を作る絶縁抵抗です.
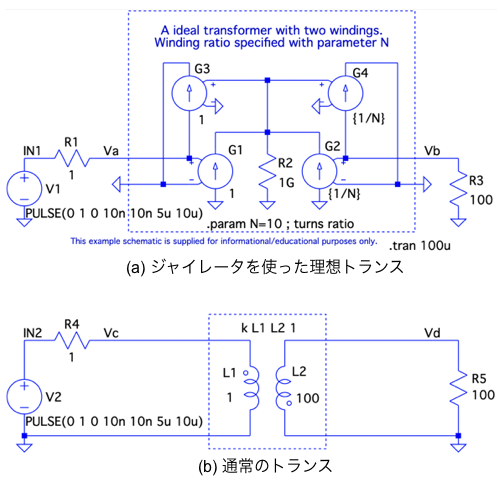
図7(a)と図6を比べると,G2とG4からなるジャイレータの電流は,図6のi2とi3に相当する電流と逆方向です.これでG1とG3のジャイレータの伝送行列は「K1=1」,「G1=1」であり,G2とG4のジャイレータの伝送行列は「K2=-N」,「G2=-1/N」となります.同様に電流の向きが違うため図7(b)のL2のコイルは図5と比べると極性(ドットの位置)が逆になります.
Nは電圧源側と負荷側の巻線比を表し,「.param N=10」で与えています.これで負荷側の巻線は電圧源側の巻線の10倍になります.コイルのインダクタンスは巻き数比の2乗に比例するため,図7(b)のL1とL2のインダクタンスは「L1=1H」,「L2=100H」となります.またトランスは無限の結合係数(k=1)とし,図7(b)の2つのコイルは無損失とします.
図8は,図7(a)と図7(b)のシミュレーション結果です.このシミュレーションはV1とV2の振幅が1Vの矩形波を入力したとき,電圧源側のVaとVc,負荷側のVb とVdの電圧をプロットしました.トランスの電圧源から見た入力インピーダンスは式12でR3とR5を巻き数比のN2で割った1Ωとなります.R1とR4は同じく1Ωですから,VaとVcは抵抗の分圧回路で0.5Vの矩形波になります.トランスの負荷側の電圧VbとVdは,電圧源側のVaとVcの電圧を反転してN倍した値となりますので,-5Vの振幅となります.図8の上段と下段は同じ波形であり,図7(a)は理想トランスとして機能していることが分かります.
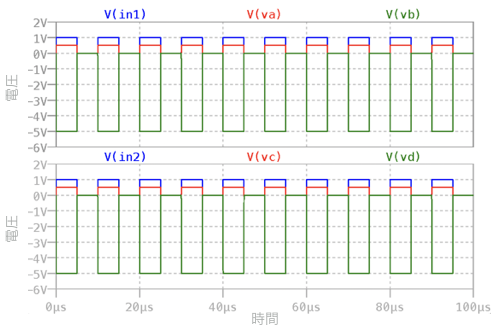
2つの結果は同じになる.
以上解説したように,1つのジャイレータへ負荷を接続したときの入力インピーダンスは,負荷と逆回路の特性が得られ,コンデンサを負荷にすると大きな値のコイルになります.また2つのジャイレータを縦続接続すると理想トランスとして機能します.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice6_012.zip
●データ・ファイル内容
IdealInductor.asc:図3の回路
IdealInductor.plt:図3のプロットを指定するファイル
IdealTransformer2.asc:図7の回路
IdealTransformer2.plt:図7のプロットを指定するファイル
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










