RCノッチ・フィルタ

図1は,特定の周波数成分を減衰させる可変抵抗器付きノッチ・フィルタです.IN端子に入力信号を加え,OUT端子から出力します.この回路には特性を調整するための10kΩの可変抵抗器が接続されています.この可変抵抗器がセンタ位置にあるときを基準として,可変抵抗器を左側に回したときの特性の変化の説明として適切なのは,(a)~(d)のどれでしょうか.ただし,可変抵抗器はセンタ位置のときに「R2=R3」となり,左に回したときは「R2:R3が1:9」になるものとします.
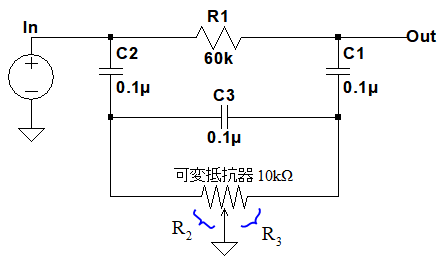
可変抵抗器を調整したときの特性の説明として,適切なのは(a)~(d)のどれ?
(a) ノッチ周波数が高くなる
(b) ノッチ周波数が低くなる
(c) ノッチ周波数での減衰量が小さくなる
(d) ノッチ周波数での減衰量が大きくなる

図1のフィルタのノッチ周波数は,R2とR3の積の平方根に逆比例します.可変抵抗器の位置とR2,R3の関係を考えれば答えが分かります.
可変抵抗器がセンタのとき,R2とR3の値は共に5kΩです.可変抵抗器を左に回したときは設問から「R2=1kΩ」で「R3=9kΩ」となります.可変抵抗器がセンタのとき,R2とR3の積の平方根は5kΩですが,可変抵抗器を左に回したときのR2とR3の積の平方根は3kΩになります.図1のフィルタのノッチ周波数はR2とR3の積の平方根に逆比例するので,可変抵抗器を左に回したときのほうがノッチ周波数は高くなります.
●ツインT・ノッチ・フィルタ
図2は,RCノッチ・フィルタとして最も有名な,ツインT・ノッチ・フィルタです.
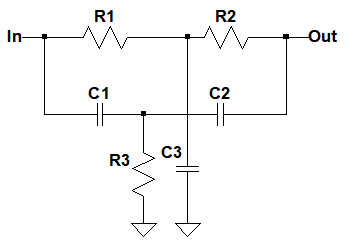
ノッチ周波数を可変したい用途には使用しにくい.
RCノッチ・フィルタとして動作するためには,それぞれの素子の定数は「C1=C2=C」,「C3=2C」で,さらに「R1=R2=R」,「R3=R/2」という関係を満足する必要があります.ノッチ周波数(fn)は式1で表されます.
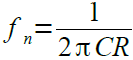 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
ツインT・ノッチ・フィルタでノッチ周波数を変更する場合,R1,R2,R3の3本の抵抗をすべて変更する必要があります.そのため,ノッチ周波数を可変したい用途には使用しづらく,図1の可変抵抗器付きノッチ・フィルタが便利です.
●ノッチ周波数を可変できるRCノッチ・フィルタ
図1の回路は可変抵抗器によりノッチ周波数を可変することができる可変抵抗器付きノッチ・フィルタです.それぞれの素子の定数は「R1=6(R2+R3)」,「C1=C2=C3=C」とする必要があります.ノッチ周波数(fn)は式2で表されます.
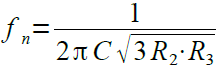 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
図1の定数で「R2=R3=5kΩ」のとき,ノッチ周波数は184Hzとなります.また,「R2=1kΩ,R3=9kΩ」のとき,ノッチ周波数は306Hzとなります.図3は,図1の回路をシミュレーションするための回路です.
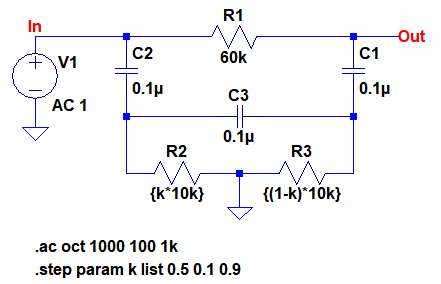
可変抵抗器を2本の抵抗で表現し,kで可変抵抗器の位置を指定する.
可変抵抗器は,2本の抵抗で表現しています.そして,R2の値を「k*10k」とし,R3の値を「(1-k)*10k」としています.可変抵抗器がセンタのときは「k=0.5」とし,可変抵抗器を左に回したときは「k=0.1」とすれば,問題と同じ条件になります.図3ではkの値を「.step」コマンドで0.5,0.1,0.9と変化させています.式2からわかるように「R2=1kΩ,R3=9kΩ,R2=9kΩ,R3=1kΩ」ではノッチ周波数は同じになります.つまり「k=0.1」と「k=0.9」は同じ周波数特性になるはずですので,それもシミュレーションで確認します.
図4が図3のシミュレーション結果です.「k=0.5」のときのノッチ周波数は184Hzで「k=0.1」と「k=0.9」のときのノッチ周波数は306Hzとなっており,計算結果と一致しています.
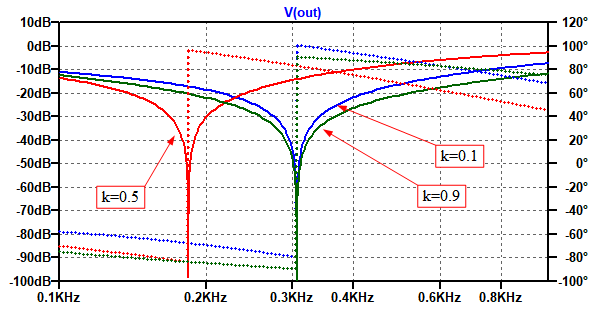
それぞれのkの値のときのノッチ周波数は計算結果と一致している.
図5は,LTspiceのサンプル・ファイル(ドキュメント\LTspiceXVII\examples\Educational\notch.asc)です.基本的には図3と同じですが「.step」コマンドでkを変更する替りに,kの異なる複数の回路を1つの回路図に置いたものです.kとしては0.5,0.05,0.005,0.0005の5種類を同時にシュミレーションするようになっています.
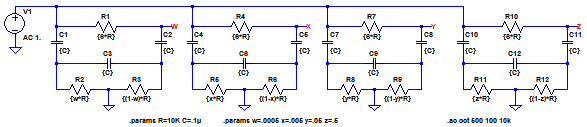
kの異なる複数の回路を1つの回路図に置いたもの.
図6は,図5のRCノッチ・フィルタのシミュレーション結果です.kの値を極端に小さくすることで,ノッチ周波数の可変幅がかなり広くなっていることが分かります.
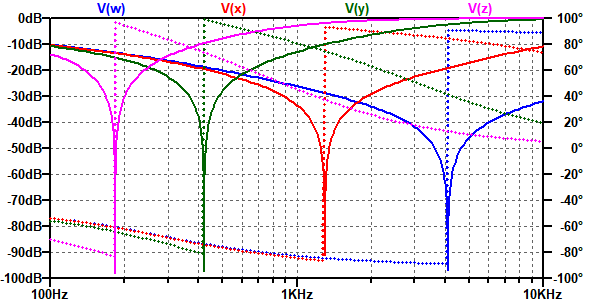
kの値を極端に小さくすることで,ノッチ周波数の可変幅がかなり広くなる.
●周波数可変RCノッチ・フィルタを使いやすくする
図1の回路は,可変抵抗器を左右どちらに回してもノッチ周波数が高くなります.そのため,周波数調整として可変抵抗器の半分しか使用できず,あまり使いやすくありません.そこで,図7のようにR4とR5の2本の固定抵抗を追加します.このようにすると,可変抵抗器の可変範囲をすべて周波数調整に使用できるようになります.
R2とR3で表現した可変抵抗器の値を2kΩに変更し,R4を1kΩ,R5を7kΩとします.このように設定することで「k=0」としたときのノッチ周波数は306Hzになり「k=1」としたときのノッチ周波数は200Hzになります.図7ではkを0から1まで0.2ステップで変化させてシミュレーションを行います.なお,R2,R3の値としてそれぞれ1mΩを加算していますが,これは「k=0とK=1」のときに抵抗値が0Ωになってしまうのを防ぐためです.
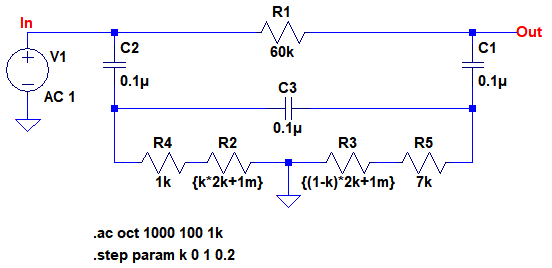
R4,R5の2本の固定抵抗を追加することで,可変抵抗器の可変範囲をすべて利用できる.
図8は,図7のシミュレーション結果です.「k=0」から「k=1」までの可変抵抗器の可変範囲すべてを使用して,ノッチ周波数を変化させることができることが分かります.
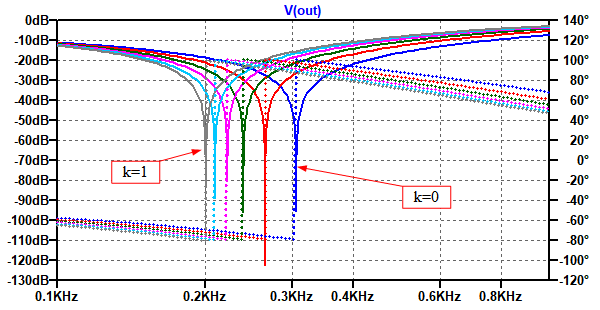
「k=0」から「k=1」までの可変範囲すべてで,ノッチ周波数を変化させることができている.
以上,ノッチ周波数を可変できるRCノッチ・フィルタについて解説しました.
Paul Horowitz,Winfield Hill(著) The Art of Electronics 1989年
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice6_007.zip
●データ・ファイル内容
notch_step.asc:図3の回路
notch.asc:図5の回路
notch.plt:図6のグラフを描画するためのPlot settinngsファイル
notch_imprv.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










