サーミスタを使用した温度測定回路

■問題
アナログ回路 ― 基礎

小川　敦　Atsushi Ogawa

　図1左は，サーミスタを使用した，温度変化を電圧変化に変換する回路です．図1右がこの回路で使用しているサーミスタの温度と抵抗値の関係を示したグラフです．この回路で，温度25℃のとき，Vt端子の電圧は0.5Vでした．それでは，温度が0℃のときのVt端子の電圧として最も近いのは(a)～(d)のどれでしょうか．

図1　サーミスタを使用した温度変化を電圧変化に変換する回路
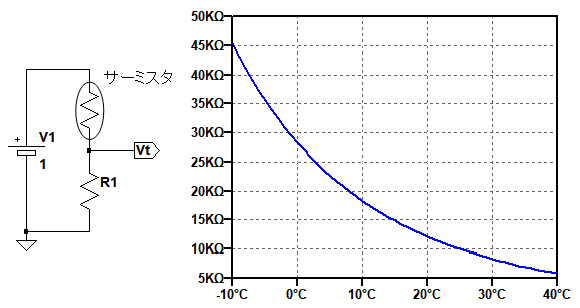
温度が0℃のときのVt端子の電圧は？

(a)0.13V　(b)0.26V　(c)0.74V　(d)0.87V

■ヒント

　サーミスタ(Thermistor:Thermal Sensitive Resistor)は，温度によって抵抗値が大きく変化する性質をもっており，温度が上がると抵抗値が大きくなるPTC(Positive Temperature Coefficient Thermistor)サーミスタと，小さくなるNTC(Negative Temperature Coefficient Thermistor)サーミスタの2種類があります．図1のサーミスタは温度が上がると抵抗値が小さくなります．その抵抗値は，指数的に変化していますが，グラフから25℃のときの抵抗値と0℃のときの抵抗値を読み取れば，答えは簡単に計算できます．

■解答

(b)0.26V

　図1のグラフから，サーミスタの25℃の抵抗値は10kΩであることが分かります．25℃でのVt端子の電圧が0.5VとV₁の半分になっていることから，R₁の値はサーミスタの抵抗値と同じ10kΩであることが分かります．また，サーミスタの0℃のときの抵抗値は，約28kΩと読み取れます．Vtの電圧は，サーミスタの抵抗値(Rt)とR₁で，V₁の電圧を分圧したものなので「Vt=1*R₁/(R₁+Rt)≒0.26V」と計算できます．したがって正解は(b)の0.26Vです．

■解説

●サーミスタの温度特性
　サーミスタには，温度が上がると抵抗値が小さくなるNTCサーミスタと，温度が一定値以上に上がると抵抗値が急激に大きくなるPTCサーミスタがあります．温度計のような用途には，一般的にNTCサーミスタが使用されます．NTCサーミスタの抵抗値は，温度に対して指数的に変化しますが，近似的に式1で表すことができます．

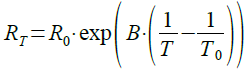・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　ここで，R₀は温度T₀（一般的には25℃）のときの抵抗値で，Tは絶対温度です．そして，Bは，サーミスタの温度に対する抵抗値の変化の傾きを表し，B定数と呼ばれています．B定数自身も温度で若干変化しますが，温度範囲を限定すれば定数とみなせます．メーカの仕様書には，代表的な温度におけるB定数と，R₀が記載されています．

●LTspiceでサーミスタの特性を再現する
　LTspiceでは，抵抗値に数式を使用することができるため，サーミスタの温度特性を再現することができます．一例として，25℃の抵抗値であるR₀が10kΩで，B定数が3380KというサーミスタをLTspice上に再現し，特性をシミュレーションします．
　図2がサーミスタの特性をシミュレーションするための回路図です．「.paramコマンド」でRというパラメータを数式を使用して定義しています．この数式は式1に定数を代入したものです．数式中のTEMPはシミュレーションする温度(℃)の値に置き換えて計算されます．「.stepコマンド」で温度を-10℃から40℃まで1℃ステップで変化させ，DC動作点解析を行います．

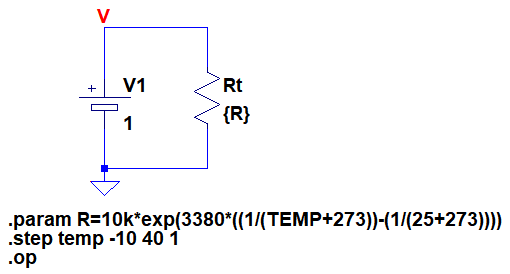
図2　LTspice上に再現したサーミスタの特性をシミュレーションする回路
R₀が10kΩでB定数が3380Kというサーミスタを表している．

　図3が再現したサーミスタの温度特性です．Rtの両端電圧をRtに流れる電流で割ることで，抵抗値を表示しています．温度変化に対して指数的に抵抗値が変化していることが分かります．

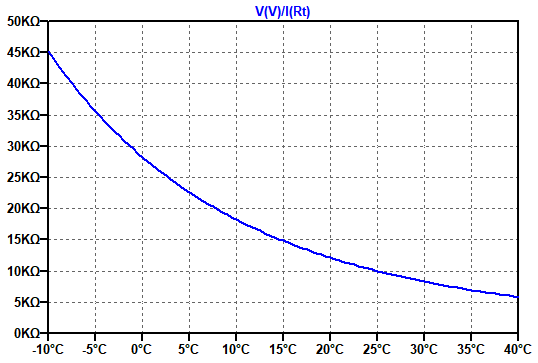
図3　LTspiceで再現したサーミスタのシミュレーション結果
温度に対して指数的に抵抗値が変化している

●温度に対する出力電圧の変化を直線に近づける
　サーミスタを使用して温度を計測する場合，温度に対して直線的に変化する電圧が得られるほうが望ましい場合があります．そのようなとき，図1のように一定の電圧源にサーミスタと抵抗を直列に接続した回路とすることで，電圧変化を簡易的に直線化することができます．図1の回路で電圧変化が直線に近づく理由を，図4を使用して考えてみます．図4は1Vの電圧をR₁とR₂で分圧する回路です．

図4　電圧変化が直線に近づく理由を考えるための回路
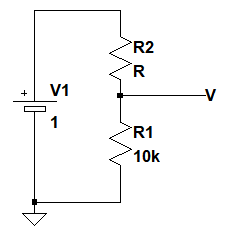
1Vの電圧をR₁とR₂で分圧している．

　この回路の出力電圧(V)は式2で計算することができます．

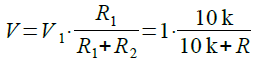・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　図5は，式2のRを45kから5kまでリニアに変化させたときのVをプロットしたものです．

図5　式2でRを45kから5kまでリニアに変化させたときのV
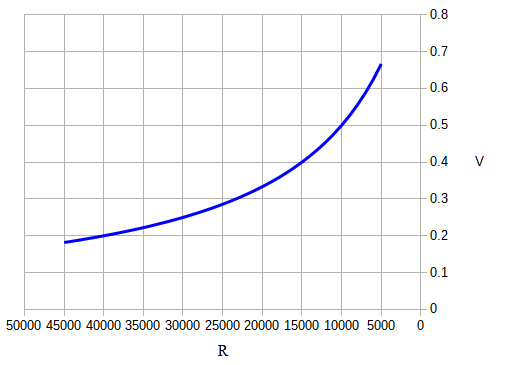
Rが小さくなると，Vの変化率が大きくなる

　Rが小さくなると，Vの変化率が大きくなることが分かります．ここで，図3のサーミスタの特性を見ると，高温で抵抗値が小さくなると，抵抗値の変化率が小さくなっていることが分かります．図4のR₂の代わりにサーミスタを使用すると，高温で抵抗値が小さなったときに，抵抗の変化率が小さくなっても，電圧の変化率が大きくなることで打ち消すことができます．そのため，温度変化に対する電圧変化を直線に近づけることができます．この回路は簡易リニアライズ回路と呼ばれ，サーミスタの応用回路として広く使用されています．

●簡易リニアライズ回路の温度と出力電圧の関係をシミュレーションする
　図6は，図4のR₂をサーミスタに置き換えた，簡易リニアライズ回路で，-10℃から40℃まで温度を変えたときの出力電圧をシミュレーションするための回路です．

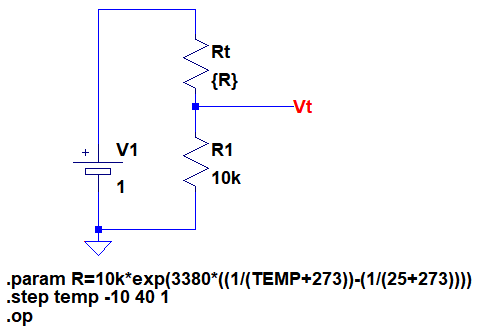
図6　簡易リニアライズ回路の温度特性をシミュレーションする回路
温度を-10℃から40℃まで変化させる．

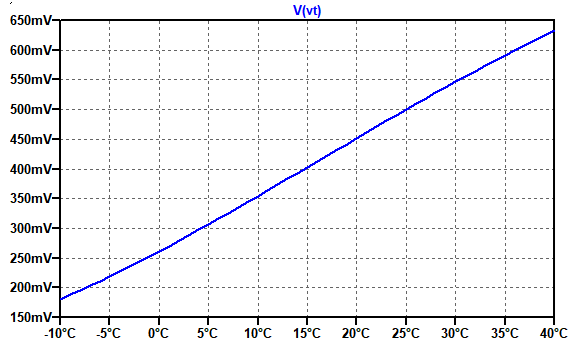
　図7は，図6の出力電圧の温度特性です．温度に対して出力電圧が直線的に変化していることが分かります．

図7　簡易リニアライズ回路の温度特性温度に対して出力電圧が直線的に変化している

●簡易リニアライズ回路の抵抗値の選び方
　簡易リニアライズ回路は，すべての温度範囲で直線化することはできません．そのため，使用温度範囲を限定し，その温度範囲に適した抵抗値を選択する必要があります．
　図8は，図6のR₁の値を1.3kΩ,10kΩ,47kΩの3種類に変化させ，温度範囲を-40℃から100℃に広げたシミュレーションを行うための回路です．

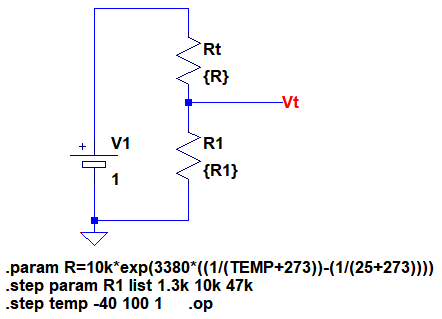
図8　簡易リニアライズ回路でR₁の値を変えたシミュレーションを行う回路温度は-40℃から100℃まで変化させる

　図9は，図8のR₁の値を変化させたときのシミュレーション結果です．下段が出力電圧のカーブで，上段は出力電圧カーブの傾きを表示しています．この傾きの値の変化が少ないほど，出力電圧の直線性が良いことを表しています．図9より，サーミスタを使用する温度範囲が高温側の場合はR₁の値を小さくし，低温側の場合は大きくすればよいことが分かります．

図9　図8のR₁の値を変化させたときのシミュレーション結果
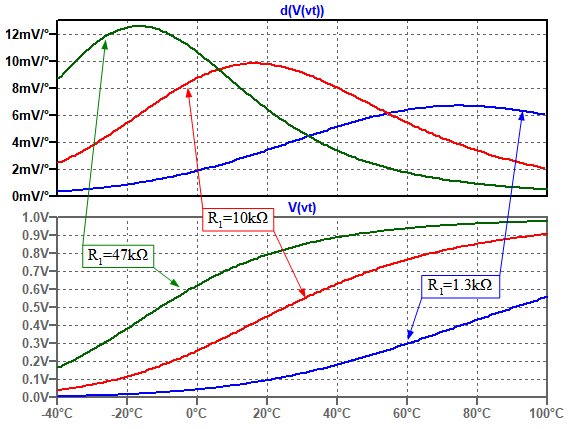
下段が出力電圧のカーブで，上段は出力電圧カーブの傾きを表示している．

　以上，サーミスタを使用した温度測定回路について解説しました．今回は簡易リニアライズ回路を紹介しましたが，マイコンを使用できる場合は，サーミスタに定電流を流し，発生した電圧をAD変換後，計算式を使ってリニアライズを行った方が，広い温度範囲を精度よく測定することができます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice5_033.zip

●データ・ファイル内容
Thermistor.asc：図2の回路
Temp-10_40.asc：図6の回路
Temp-10_40.plt：図7のグラフを描画するためのPlot settinngsファイル
Temp-40_100.asc：図8の回路
Temp-40_100.plt：図9のグラフを描画するためのPlot settinngsファイル