エミッタ接地回路の出力抵抗の算出

図1は,NPNトランジスタ(Q1)を使ったエミッタ接地回路です.Q1のコレクタ電流(IC)とベース電流(IB)の比である電流増幅率(β)は100です.図2は,IBが4つの電流(a)~(d)のとき,VCEを0V~10Vまで変化させたときのICの変化をプロットした図です.図2の特性の場合,コレクタからみたトランジスタの出力抵抗が一番高いのは,(a)~(d)のうちどれでしょうか.
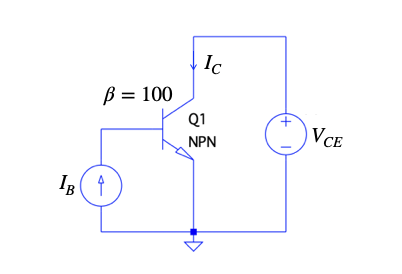
コレクタからみた出力抵抗を測定する.
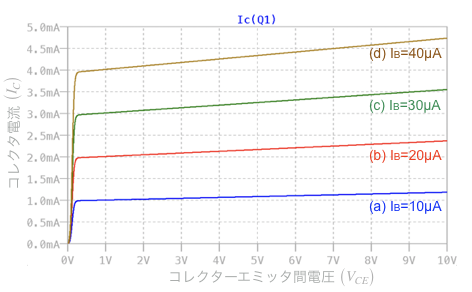
出力抵抗が最も高いのはどの条件か?
(a)IB=10μA (b)IB=20μA (c)IB=30μA (d)IB=40μA
トランジスタのコレクタは,電流出力なので,出力抵抗は高い方が良い性能といえます.ここではその出力抵抗の算出方法を解説します.トランジスタの出力抵抗は,オームの法則より,「コレクターエミッタ間電圧の僅かな変化(ΔVCE)」に対する「コレクタ電流の僅かな変化(ΔIC)」の比となります.なので,図2のプロットの傾きの大きさから出力抵抗を検討すると分かります.
コレクタからみた出力抵抗は「ro=ΔVCE/ΔIC」です.同じΔVCEのとき,出力抵抗が小さくなるのは,ΔICが小さいときです.4つの条件のプロットではIB=10μAの傾きが一番小さいので,この条件のとき出力抵抗が高くなります.
●コレクタからみた出力抵抗について
トランジスタのコレクタは,電流出力であり,コレクタ電流(IC)は,ベース電流(IB)へ電流増幅率(β)を乗じた「IC=βIB」となります.よって,コレクタ電流はベース電流と電流増幅率に依存した電流源とみなせます.理想トランジスタのコレクタからみた出力抵抗は,コレクタの電圧に関係なくβIBの電流を流す電流源なので,出力抵抗は無限大です.しかし,実際は図1のプロットのように,コレクタ電圧の変化に対し,コレクタ電流が変化します.この変化分が出力抵抗「ro=ΔVCE/ΔIC」となります.図1は,シミュレーションのプロットですが,実デバイスの出力抵抗もカーブ・トレーサなどを使って図1のDC特性を測り「ro=ΔVCE/ΔIC」で求めることができます.
●出力抵抗が生まれる原因
図3は,出力抵抗が生まれるメカニズムを解説するものです.青の領域がN型半導体,赤の領域がP型半導体で,NPNトランジスタを表しています.ベースとエミッタ間にはトランジスタをオンにするVBEの電圧があり,約0.7Vが一般的な値です.コレクタとエミッタ間にはVCEの電圧があり,図2のプロットでは0V~10Vまで変化させています.この2つの電圧により,ベースのP型とコレクタのN型のダイオードには,逆バイアス電圧のVCBが加えられます.数値例をあげると「VBE=0.7V,VCE=5V」のとき,逆バイアス電圧のVCBは「VCB=VCE-VBE=4.3V」となります.VCBは,VCEにより逆バイアス電圧が変化するため,図3のVCB小のとき,空乏層の幅が狭く,VCB大になると空乏層の幅が広くなります.この空乏層幅の変化は,実効ベース幅に影響し,WB1,WB2のように変化します.
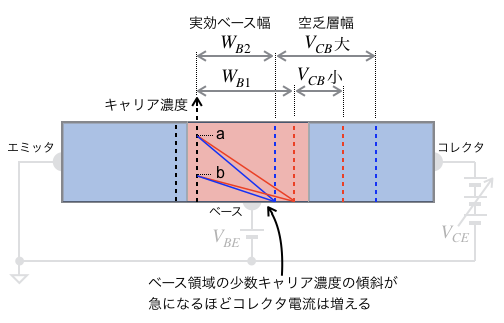
VCBの電圧変化で実効ベース幅が変わり,コレクタ電流が変化するため出力抵抗が生まれる.
NPNトランジスタは,ベース領域の少数キャリア濃度は,エミッタ側にある空乏層の端で高く,コレクタ側の空乏層の端で低くなります.また,少数キャリア濃度の傾斜が急になると(青の実線の傾斜)コレクタ電流が増え,傾斜が緩くなると(赤の実線の傾斜)コレクタ電流は減ります.この電流の変化(ΔIC)が出力抵抗を生む原因となります.
ベース電流による出力抵抗の違いは,図3のベース領域のaとbで解説できます.aはベース電流が大きく少数キャリア濃度が高いときを表し,bはその逆のベース電流が小さく,少数キャリア濃度が低い状態を表しています.aの状態では実効ベース幅の変化による少数キャリア濃度の傾斜の変化が大きくなり,コレクタ電流の変化も大きくなります.bの状態では,少数キャリア濃度の傾斜が緩いため,実効ベース幅が変化しても傾斜の変化は小さくなり,コレクタ電流の変化は小さくなります.これにより,図2のプロットように,ベース電流が小さいほどコレクタ電流の変化(ΔIC)が小さくなり,出力抵抗が高くなります.
以上の実効ベース幅が変化することを,ベース幅変調効果と呼び,1952年にジェームス M アーリー博士(James M.Early)により発表されました.
●出力抵抗の算出
図4は,図1の回路で,ベース電流(IB)が大きいときと小さいときの2つのプロットを示します.先ほどのベース幅変調効果により,出力抵抗(ro)は,IBが大きいとき(aのプロット)に出力抵抗は低くなり,IBが小さいとき(bのプロット)に大きくなります.VCE-IC特性の接線をX軸の負側まで延ばすと,ある1点の電圧(VA)で交差します.この電圧をジェームス M アーリー博士の名にちなんでアーリー電圧と呼びます.
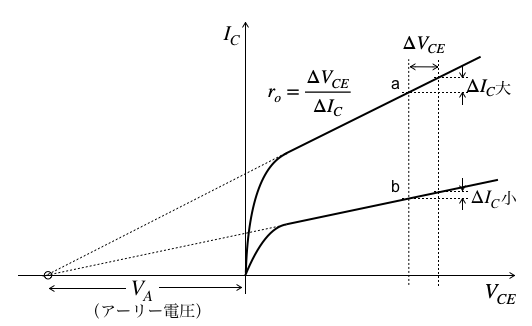
接線をX軸の負側まで延ばした交点がアーリー電圧となる.
アーリー電圧(VA)は,トランジスタのコレクターエミッタ間電圧(VCE)より十分大きな値となることから,式1で近似できます.
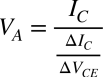 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
式1より,出力抵抗は式2となり,アーリー電圧とコレクタ電流から求まります.
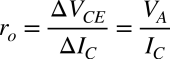 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
(a)~(d)のベース電流(IB)と電流増幅率(β=100)を使ってコレクタ電流を求め,アーリー電圧(VA)を50Vとすると,出力抵抗は次の値となります.
(a)IB=10μAのとき,IC=1mAなので,ro=50V/1mA=50kΩ
(b)IB=20μAのとき,IC=2mAなので,ro=50V/2mA=25kΩ
(c)IB=30μAのとき,IC=3mAなので,ro=50V/3mA=16.7kΩ
(d)IB=40μAのとき,IC=4mAなので,ro=50V/4mA=12.5kΩ
●コレクタからみた出力抵抗をLTspiceで確認する
図5は,図1をシミュレーションする回路です.シミュレーションは,DC解析を用い,図1のVCEに相当するV1の電圧を0V~10Vを10mVの間隔でスイープさせます.また,IBに相当するI1の電流は,10μから40μAを10μAステップで変化させます.Q1のトランジスタのアーリー電圧は50Vとし,そのモデルパラメータを「.model NPN NPN (VAF=50)」で与えています.
回路図中には「.MEAS」でVCEが5Vのコレクタ電流をres1へ代入,VCEが6Vのコレクタ電流をres2へ代入し,res1とres2を使って計算した出力抵抗をres3へ代入します.
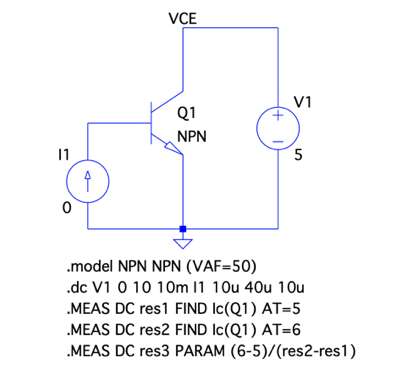
図2は,図5をシミュレーションしたときのVCE-IC特性のプロットです.また,そのときの「.MEAS」の結果は,図6となります.これは,回路図上で「Ctrl+L」とするとログファイルが開き,そこに記録されています.図6の「step1がIB=10μA」,「step2がIB=20μA」,「step3がIB=30μA」,「step4がIB=40μA」です.res3より「.MEAS」で計算した出力抵抗は,先ほどの式2を使った計算と一致します.

出力抵抗は式2を使った計算値と一致する.
図7は,LTspiceの導関数「d()」を使ってΔVCE/ΔICの出力抵抗をプロットしました.ここでも式2を使って計算した値と一致し「IB=10μA」のときの出力抵抗が一番大きくなることが分かります.
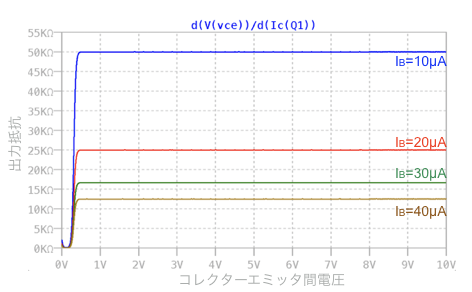
出力抵抗は,式2を使った計算結果と一致する.
解説したように,トランジスタのコレクタからみた出力抵抗は,ベース幅変調効果により発生し,VCE-IC特性の測定結果より具体的な値を求めることができます.また,アーリー電圧が分かっているときは,式2を使って簡単に求めることができます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice5_020.zip
●データ・ファイル内容
Output_Resistance.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










