コイルと抵抗を組み合わせた特性

■問題
電気回路 ― 基礎

小川　敦　Atsushi Ogawa

　図1は，1mHのコイルと6.2Ωの抵抗を組み合わせた回路です．IN端子に接続されている信号源(V₁)から正弦波信号を加えて，OUT端子の信号レベルを測定します．V₁の周波数を1Hzから10kHzまで変化させ，入力信号の大きさを基準（0dB）として，出力信号の大きさをグラフにしました．そのグラフとして，正しいのは図2の(a)～(d)のどれでしょうか．

図1　1mHのコイルと6.2Ωの抵抗を組み合わせた回路
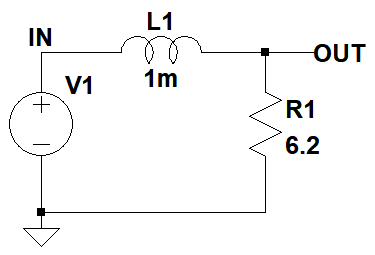
V₁の周波数を1Hzから10kHzまで変化させる．

図2　図1の出力信号のグラフ
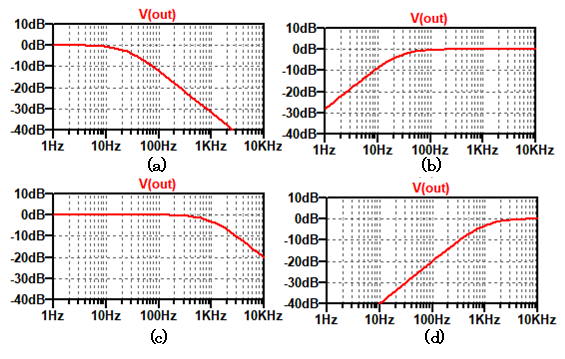
正しいグラフはどれでしょうか？

(a)のグラフ　(b)のグラフ　(c)のグラフ　(d)のグラフ

■ヒント

　まず，基本的な性質として，コイルが周波数によって出力信号の大きさがどのように変化するかを考えます．次にコイルと抵抗の値から，グラフの変曲点の周波数を計算すれば正解が分かります．

■解答

(c)のグラフ

　コイルは，基本的な性質として，加えた交流信号の周波数が低いほど電流が流れやすくなり，周波数が高いほど電流が流れにくなります．そのため，図1の回路のOUT端子の信号レベルは，周波数が高いほど小さくなります．そのため，正解は(a)か(c)のどちらかです．また，図1の回路のローパス・フィルタとしてのカットオフ周波数を計算すると「R₁/(2πL)=6.2/(2π1m)≒1kHz」となります．カットオフ周波数が1kHzとなっているのは(c)のグラフのため，正解は(c)ということになります．

■解説

●コイルに交流信号を加えた時の性質
　コイルは，導体を巻いたものなので，直流電圧を加えると非常に大きな電流が流れます．つまり，直流電圧に対する抵抗は非常に小さくなっています．しかし，交流信号を加えた場合，その周波数が高くなるほど電流が流れにくくなります．言い換えると，加える電圧の周波数が高いほど，交流抵抗（インピーダンス）が大きくなることになります．また，コイルの巻線に電流を流すと磁界が発生し，その強さは電流に比例します．その比例定数がインダクタンスです．そこで，インダクタンス値がLのコイルを使用した場合，そのコイルのインピーダンス(Z_L)の絶対値と周波数(f)の関係は，式1で表されます．

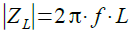・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　図3は図1のコイルをインピーダンスZ_Lとして書き換えた回路図です．

図3　コイルをインピーダンスZ_Lに書き換えた回路
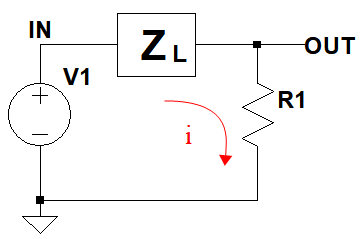
V_OUTはV₁をZ_LとR₁で分圧したものになる．

　この回路でR₁に流れる電流(i)は式2で表されます．

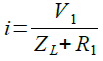・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　OUT端子の電圧(V_OUT)は，iとR₁を掛けたものなので，式3で表すことができます．

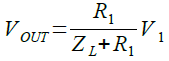・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　つまり，V_OUTは，V₁をZ_LとR₁で分圧したものになります．式3より，V_OUTは，Z_LがR₁よりも十分小さい周波数のときV₁と等しくなります．また，周波数が高くなるほどZ_Lは大きくなるので，V_OUTが小さくなることも分かります．つまり，図1の回路は，高い周波数の信号が減衰する，ローパス・フィルタとして動作することが分かります．
　ここで，Z_Lの絶対値がR₁と同じになる周波数をカットオフ周波数(f_C)と呼びます．カットオフ周波数以上の信号が減衰することになります．カットオフ周波数(f_C)は式4を変形して，

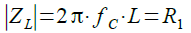・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　式5のように求められます．

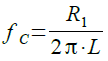・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　図1の定数を代入すると，式6のように，カットオフ周波数は約1kHzになります．

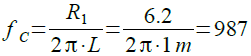・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　カットオフ周波数でのV_OUTの信号の大きさは式3で計算することができます．ただし，分母となるコイルのインピーダンスと抵抗を加算した合成インピーダンスは，図4のように抵抗とコイルのインピーダンスを頂点とする四角形の，対角線の長さになります．

図4　カットオフ周波数での合成インピーダンスの計算のしかた
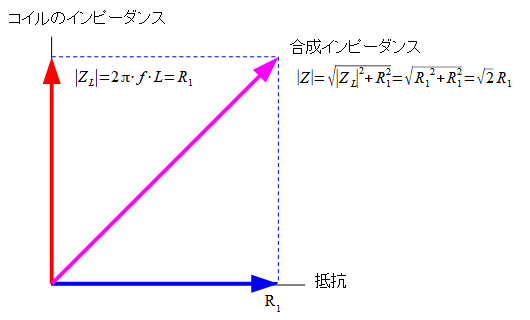
合成インピーダンスの絶対値は√2 R₁になる．

　そのため，合成インピーダンス(Z)の絶対値は式7のように「√2 R₁」になります．

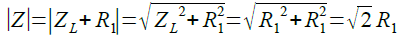・・・・・・・・・・・・・・・(7)

　式7を式3に代入すると，式8のように，カットオフ周波数でのOUT端子の出力は入力信号の「1/√2」となり，デシベルに変換すると3dB減衰することが分かります．

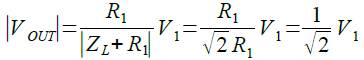・・・・・・・・・・・・・・・・・・(8)

●LRローパス・フィルタのシミュレーション
　図5は，図1のLRローパス・フィルタをシミュレーションするための回路図です．AC解析で1Hzから10kHzまでの周波数特性をシミュレーションします．

図5　LRローパス・フィルタをシミュレーションするための回路
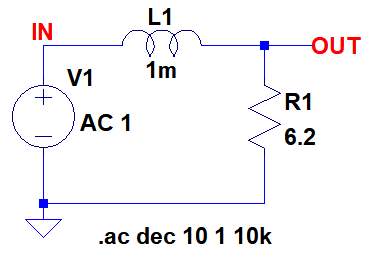
1Hzから10kHzまでの周波数特性をシミュレーションする．

　図6がOUT端子の出力レベルのシミュレーション結果です．出力レベルが3dB減衰するカットオフ周波数は式6で計算したように約1kHzとなっていることが分かります．これは，図2の(c)のグラフと同じ結果です．

図6　LRローパス・フィルタのシミュレーション結果
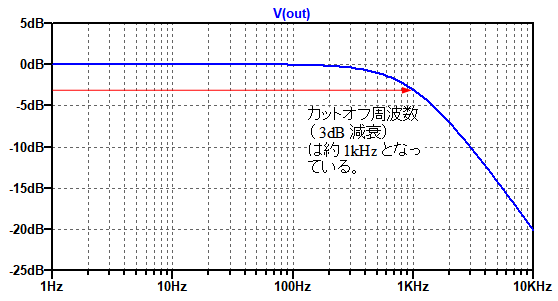
カットオフ周波数は約1kHzになっている．

●LCRローパス・フィルタのシミュレーション
　図5の回路にコンデンサを追加して，LCRフィルタにするとフィルタとしての減衰特性を急峻にすることができます．図7は，LRフィルタとLCRフィルタの特性を比較するための回路図です．OUT1がLRフィルタの出力でOUT2がLCRフィルタの出力となっています．

図7　LRフィルタとLCRフィルタの特性を比較するための回路
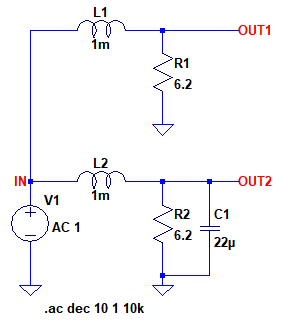
OUT1がLRフィルタの出力でOUT2がLCRフィルタの出力．

　図8は，図7のシミュレーション結果です．OUT2のLCRフィルタのほうが減衰特性が急峻になっていることが分かります．

図8　LRフィルタとLCRフィルタのシミュレーション結果
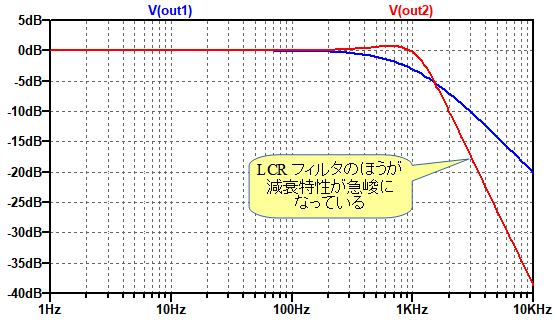
LCRフィルタのほうが減衰特性が急峻になっている．

　以上，コイルと抵抗を組み合わせた特性について解説しました．一般的にコイルはコンデンサよりも外形が大きく，価格も高いため，通常はコイルと抵抗を組み合わせたフィルタではなく，コンデンサと抵抗を組み合わせたフィルタが使用されます．ただし，大きな直流電流を流す必要のある電源回路や，非常に周波数の高い高周波回路ではコイルとコンデンサを組み合わせたフィルタが使用されます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice5_019.zip

●データ・ファイル内容
LR_LPF.asc：図5の回路
LCR_LPF.asc：図7の回路