コイルの直列接続と並列接続

図1は,3つのコイル(L1,L2,L3)に電圧源(V1)が接続された回路です.L1に,並列接続されたL2とL3が直列接続されています.この回路で0VだったV1の電圧を1ns後に1Vになるよう,ステップ状に変化させたとき,1ms後にL1に流れている電流として,最も近いのは(a)~(d)のどれでしょうか.
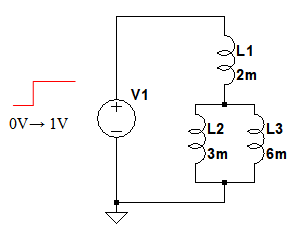
V1の初期値は0Vとなっており,初期状態ではL1~L3のコイルには電流が流れていません.また,それぞれのコイルの,直列抵抗成分は無視できるものとします.
(a)91mA (b)154mA (c)250mA (d)500mA
インダクタンスがLのコイルにVという電圧を印加したときの,t秒後の電流は「I=(V/L)*t」で計算できます.並列および直列接続された,コイルL1~L3の合成インダクタンスが分かれば,1ms後のL1の電流も簡単に計算できます.
この回路は,L2とL3が並列接続され,その合成インダクタンスとL1が直列接続されていると考えることができます.したがって3つのコイルの合成インダクタンスは「L1+(1/(1/L2+1/L3))」で計算することができます.図1の数値を代入すると合成インダクタンスは「2m+(1/(1/3m+1/6m)=4m」となります.
インダクタンスがLのコイルにVという電圧を印加したときの,t秒後の電流の式「I=(V/L)*t」に数値を代入すると「(1/4m)*1m=0.25A」となります.したがって正解はDの250mAということになります.
●コイルを直列接続したときの合成インダクタンス
コイルを直列に接続した場合,その合成インダクタンスは,それぞれのコイルのインダクタンスを足したものになります.図2は,合成インダクタンスを計算するための回路です.直列接続されたコイルに,一定の割合で変化する電流を加えます.
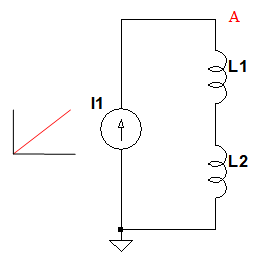
直列接続されたコイルに一定の割合で変化する電流を加える.
電流の変化率をΔI/Δtとすると,インダクタンス(L)に発生する電圧(V)は式1で表されます.
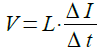 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
図2のL1,L2には同じ電流が流れます.そのため,それぞれのインダクタンスの値をL1,L2とすると,A点の電圧は式2で計算できます.
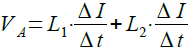 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
ΔI/Δtという電流を流したときのA点の電圧が式2となることから,合成インダクタンスをLとすると,式3が成立します.
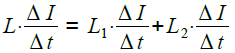 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3の両辺をΔI/Δで割ると,式4のように合成インダクタンスを求める式が完成します.
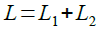 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
●コイルを直列接続したときの電圧をシミュレーションする
図3左は,1Hのコイルと2Hのコイルを直列接続したものに電流源を接続し,図3右は,1Hと2Hを足した値である3Hのコイルに電流源を接続しています.2つの電流源は共に1秒間に1A電流が増加するように設定しています.
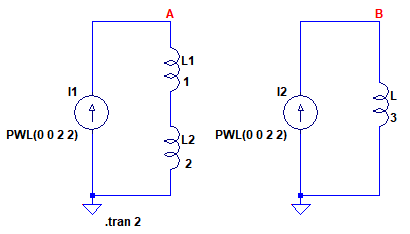
1秒間に1A増加する電流を加えたときのA点,B点の電圧を比較する.
図4は,図3のシミュレーション結果です.1Hと2Hのコイルを直列接続したA点と,3HのコイルのB点の電圧は全く同じ3Vとなっており,両者のインダクタンスが等しいことが分かります.
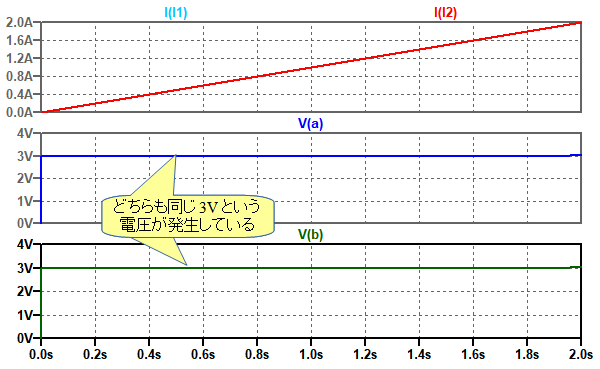
1Hと2Hのコイルを直列接続したものと3Hのコイルの電圧は全く同じ.
●コイルを並列接続したときの合成インダクタンス
図5は,コイルを並列接続したときの合成インダクタンスを計算するための回路です.
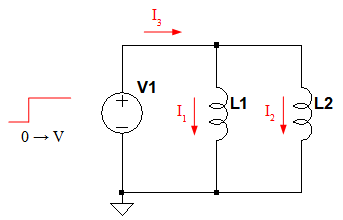
並列接続されたコイルにステップ状の電圧を加える.
コイル(L)にステップ状に変化する電圧(V)を加えたときの,時間tにおけるコイルの電流をI(t)とすると,I(t)は式5になります.
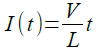 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
式5より,図5のI3は式6で計算できます.
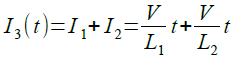 ・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
L1,L2の並列インダクタンスをLとすると,式7が成立します.
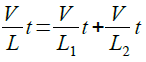 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7の両辺をV*tで割り,それぞれ逆数を取ると,式8のように,コイルを並列接続したときの合成インダクタンスを求める式が得られます.
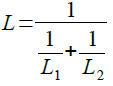 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
●コイルを並列接続したときの電流をLTspiceで確認する
図6左は,3Hのコイルと6Hのコイルを並列続し,そこに電圧源を接続しています.図6右は,左の回路の2つのコイルの合成インダクタンスの値(1/(1/3+1/6)=2H)としたコイルに電圧源を接続しています.どちらの電圧源も初期値は0Vで1ns後に1Vになるように設定しています.
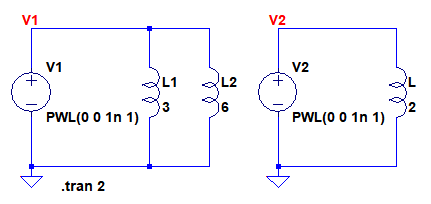
V1,V2をステップ状に変化させたときに流れる電流を比較する.
図7は,図6のシミュレーション結果です.V1とV2の電流は-を付けて符号を反転して表示しています.3Hのコイルと6Hのコイルを並列接続したものと,2Hのコイルに流れる電流はまったく同じ傾きとなっており,両者が等価であることが分かります.
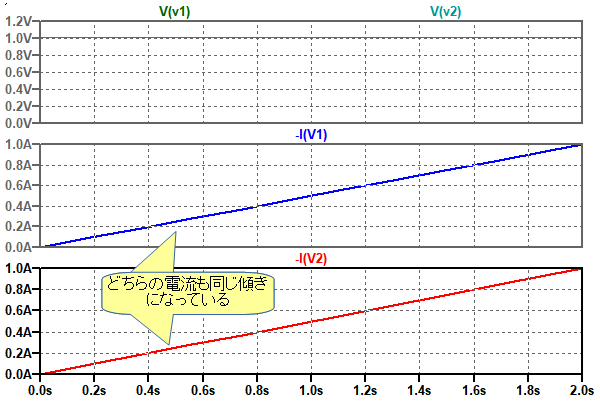
3Hと6Hのコイルを並列接続したものと,2Hのコイルに流れる電流は同じ.
●並列接続と直列接続を組み合わせたときの電流をシミュレーションする
図1の回路は,並列接続と直列接続を組み合わせたものです.そのため,この回路の合成インダクタンスは,式4と式8を組み合わせ,式9のようにして4mHと計算することができます.
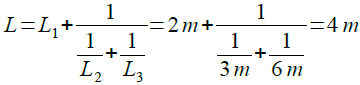 ・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・(9)
式5にこの数値を代入すると,1ms後の電流は式10のように250mAと計算できます.
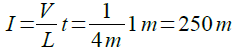 ・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
図8は,図1の回路をシミュレーションするための回路です.コイルを並列接続と直列接続の組み合わせた回路です.
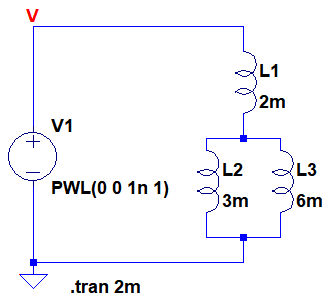
V1の電圧を1ns後に1Vになるようステップ状に変化させている.
図9は,図8のシミュレーション結果です.式10で計算したように,1ms後のL1の電流は250mAになっていることが分かります.
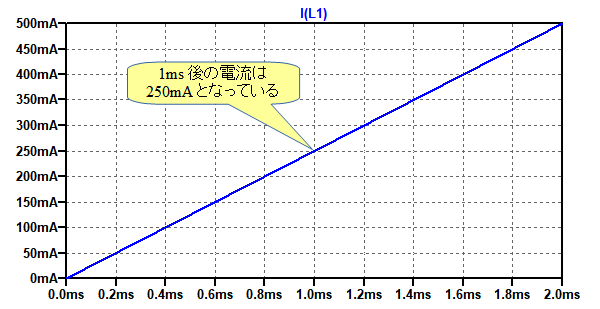
計算結果と同様に1ms後のL1の電流は250mAになっている.
このように,コイルを並列接続したり,直列接続することで,様々なインダクタンスのコイルを合成することができます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice5_015.zip
●データ・ファイル内容
inductor_S.asc:図3の回路
inductor_S.plt:図4を表示するための設定ファイル
inductor_P.asc:図6の回路
inductor_P.plt:図7を表示するための設定ファイル
inductor_S_P.asc:図8の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










