ダイオードの交流抵抗を求める

■問題
電気回路 ― 基礎

平賀　公久　Kimihisa Hiraga

　図1のダイオード(D₁)には，20μAの直流電流(I₁)と振幅1μAの正弦波による交流電流(I₂)の2つの電流の和(I_F)が流れます．V_F端子には，I_Fの変化に応じた交流電圧が現れます．I_FとV_F端子の電圧の関係は「I_F=19μAのとき，V_F=552.6mV」，「I_F=20μAのとき，V_F=553.9mV」，「I_F=21μAのとき，V_F=555.2mV」でした．この関係より，ダイオードの交流抵抗は，(a)～(d)のどれでしょうか.

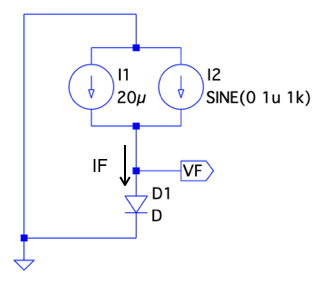
図1　ダイオード(D₁)へ直流20μA(I₁)と振幅1μAの正弦波電流(I₂)を流した回路図
V_F端子の交流電圧より求まるダイオードの抵抗はいくらか．

(a)1.3kΩ　(b)2.5kΩ　(c)27.7kΩ　(d)29.1kΩ

■ヒント

　ダイオードの中を流れるI_Fの変化と，V_F端子の交流電圧変化より，オームの法則を用いて，ダイオードの交流抵抗を求めることができます．

■解答

(a)1.3kΩ

　I₁とI₂の2つの電流源は，並列接続です．なので，ダイオードに流れる電流は，2つの電流源の和(I_F)となります．I₁が直流の20μA，I₂が振幅1μAの正弦波電流で，I_Fは，20μAを中心に±1μAの電流となります．これより,I_Fの最小値が19μAで，中心が20μA，最大値が21μAとなります．この電流変化のときの，V_F端子の電圧を求めます．I_Fが19μAのときとI_Fが20μAのときのV_Fの差は，「I_F=19μAのとき，V_F=552.6mV」，「I_F=20μAのとき，V_F=553.9mV」を使い，式1の「-1.3mV」となります．

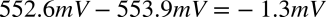・・・・・・・・・・・・・・・・・・・・(1)

　また，I_Fが21μAとI_Fが20μAのときのV_Fの差は,「I_F=21μAのとき，V_F=555.2mV」,「I_F=20μAのとき，V_F=553.9mV」を使い，式2の「1.3mV」となります．

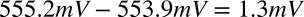・・・・・・・・・・・・・・・・・・・・・・(2)

　これより，V_Fは，553.9mVを中心に±1.3mVの交流信号となります．ダイオード(D₁)の交流抵抗は，V_Fの交流電圧とI_Fの交流電流より，式3となります．

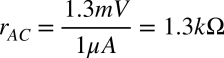・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

よって，解答は(a)の1.3kΩとなります．

■解説

●ダイオードの抵抗について
　ダイオードの順方向へ電圧を印加すると，順方向に電流が流れます．この電圧と電流の関係から，ダイオードは抵抗特性を持ちます．通常の抵抗器と違うのは，ダイオードは電圧を印加すると電流は指数関数的に増加する特性となり，電圧と電流は比例しません．この特性により，ダイオードの抵抗は，直流抵抗と交流抵抗に分けられます．
　図2は，ダイオードの直流抵抗を示しています．直流抵抗は，ダイオードの直流電圧と直流電流から計算したもので，図2のQ点とグラフ原点との青線から求めます．具体的には，直流の印加電圧(V_F1)と，そのときに流れる直流電流(I_F1)を使い，直流抵抗は「rDC=V_F1/I_F1」となります．

図2　ダイオードの直流抵抗
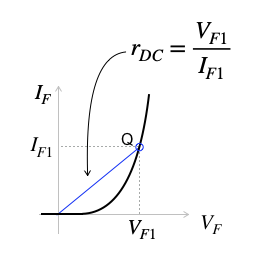
直流抵抗はQ点と原点間の傾き．

　図3は，ダイオードの交流抵抗を示しています．交流抵抗は，交流電圧変化に対する交流電流のわずかな変化から求めます．ダイオードの電流は指数関数的に増加して非線形であるため，グラフ上のQ点の位置が変わると抵抗値が変わります．交流抵抗は，Q点近くの交流電圧変化をΔV_Fとして，また，交流電流変化をΔI_Fとすれば，「rAC=ΔV_F/ΔI_F」となります．これは図3のグラフ上では，Q点での傾きを表す青線の接線から求まります．

図3　ダイオードの交流抵抗
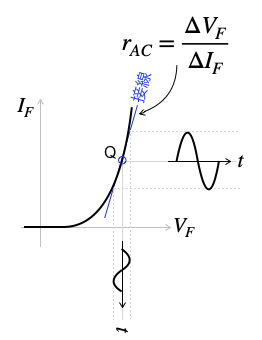
交流抵抗はQ点における接線の傾き．

●LTspiceのDC解析から交流抵抗を求める
　図4は，図1のI₁とI₂の電流源を1つの直流電流源(I3)と置き換えた回路です．この図4を使ってDC解析をします．DC解析は，直流電流源I3をスイープし，Q点での接線より交流抵抗を調べます．ここで図1のQ点は,交流信号の中心となる「I_F=20μAのとき，V_F=553.9mV」のポイントです．
　図4は，4つの「.MEASコマンド」でシミュレーションした結果から値を求めます．上から3つは，ダイオードに流れる電流が19μA，20μA，21μAのときのV_Fの電圧を調べ，res1，res2，res3の変数に入れます．この値を確かめると,ダイオードの3つの電流によるV_Fの電圧が分かります．4つ目は，LTspiceの導関数d()を使い，図3の「rAC=ΔV_F/ΔI_F」に相当するd(V(vf))/d(I(D₁))の傾きより，交流抵抗を計算させ，ダイオードの電流が20μAのときの交流抵抗をres4の変数に入れます．

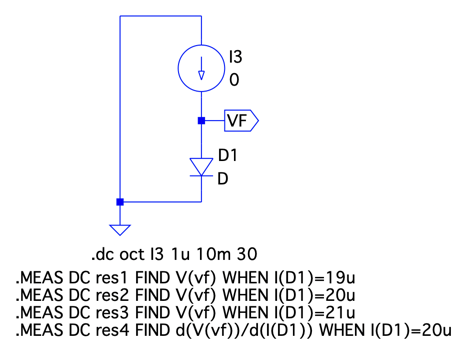
図4　ダイオードの順方向電圧と順方向電流をシミュレーションする回路

　図5は，図4のシミュレーション結果です．グラフは2つに分け，上段は，ダイオードの順方向電圧と順方向電流の特性です．下段は，d(V(vf))/d(I(D₁))の傾きより，交流抵抗を計算させた結果です．なお，シミュレーションは，電流源をスイープさせています．しかし，X軸は，V_Fの電圧へ変更してプロットしています．「I_F=20μAのとき，V_F=553.9mV」のQ点では，ダイオードの交流抵抗が，解答と同じ「rAC=1.3kΩ」となります.

図5　図4のシミュレーション結果
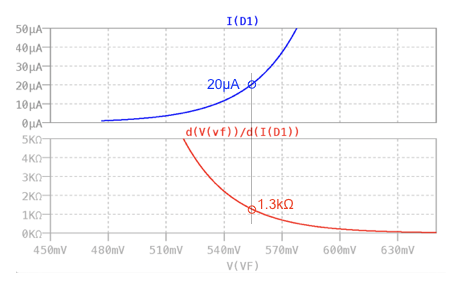
上段はダイオードの順方向電圧と順方向電流をプロットした．
下段は交流抵抗をプロットした．

　図4の回路図上で「Ctrl+L」すると，LTspiceのログ・ファイルが表示されます．このログ・ファイルの中に「.MEASコマンド」の結果があるので，より詳細な値を調べることができます．次のres1，res2，res3，res4の太字で示した値が「.MEASコマンド」で調べた結果となります．res1，res2，res3はダイオードの電流が19μA，20μA，21μAのときのV_Fの値，res4がダイオードの電流が20μAのときの交流抵抗となります．

　res1: v(vf)=0.552606 at 1.9e-05
　res2: v(vf)=0.553933 at 2e-05
　res3: v(vf)=0.555195 at 2.1e-05
　res4: d(v(vf))/d(i(d1))=1298.05 at 2e-05

●電流源の過渡解析で交流抵抗を調べる
　図6は，過渡解析の交流電圧と交流電流の振幅より交流抵抗をシミュレーションする回路です．この回路を用いて，図1と同じ20μAの直流電流(I₁)と振幅1μAの正弦波による交流電流(I₂)の2つの電流の和が，ダイオードに流れたときのV_Fの電圧振幅の変化より，交流抵抗を確かめます．回路図中の「.MEASコマンド」は，V_F端子の電圧波形のピーク・トゥ・ピーク値を調べ，正弦波交流電流のピーク・トゥ・ピーク値で除算して交流抵抗を計算します．

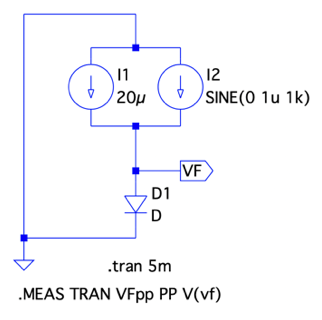
図6　交流電圧と交流電流の振幅より交流抵抗をシミュレーションする回路

　図7は，図6のシミュレーション結果です．上段がダイオードに流れる電流であり，ピーク・トゥ・ピークの電流は2μAppです．下段はV_F端子の電圧で，ピーク・トゥ・ピークの電圧は2.58mVppです．

図7　図6のシミュレーション結果

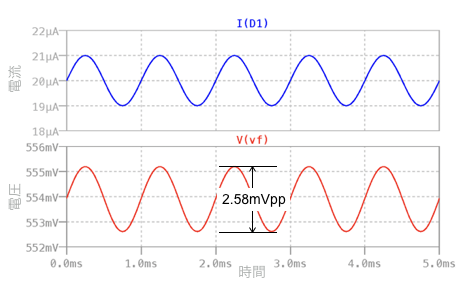
　この2つの値より，交流抵抗は式4の1.29kΩとなり，解答の1.3kΩとほぼ同じになります．

・・・・・・・・・・・・・・・・・・・・・・・・(4)

　V_F端子の電圧は「Ctrl+L」で開いたログ・ファイル中にある「.MEASコマンド」で調べた値で確かめることができます．次が，ログ・ファイル中の値で，太字がV_F端子のピーク・トゥ・ピークの電圧となります．

　vfpp: PP(v(vf))=0.00258429 FROM 0 TO 0.005

　このように，ダイオードの交流抵抗は，順方向電圧と順方向電流のDC解析より，Q点の傾きより調べることができます．この値は，交流信号を使った過渡解析の電圧振幅と電流振幅より求めた交流抵抗と同じになることを確認しました．