コンデンサの直列接続と並列接続

図1は,コンデンサC1,C2,C3に電流源(I1)が接続された回路です.C2とC3は並列接続され,そこにC1が直列接続されています.C1~C3のコンデンサの両端電圧が0Vで,I1の初期値は0Aとなっています.この回路で,0AだったI1を1ns後に1uAになるよう,ステップ状に変化させたとき,1秒後のOUT端子の電圧として近いのは,(a)~(d)のどれでしょうか.
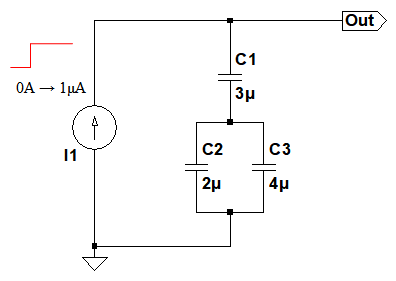
1秒後のOUT端子の電圧は?
(a)0.111V (b)0.25V (c)0.333V (d)0.5V
静電容量値(C)のコンデンサに電流(I)を印加したときの,t秒後の電圧は「V=I*t/C」で計算できます.並列と直列接続された,コンデンサC1~C3の合成容量がわかれば,1秒後のOUT端子の電圧は簡単に計算できます.
この回路は,C2とC3が並列接続され,その合成容量とC1が直列接続されています.したがって3つのコンデンサの合成容量は「1/(1/C1+1/(C2+C3))」で計算することができます.図1の数値を代入すると,合成容量は「1/(1/3μ+1/(2μ+4μ ))=2μF」となります.静電容量値(C)のコンデンサに電流(I)を印加したときのt秒後の電圧の式「V=I*t/C」に数値を代入すると「1μ*1/2μ=0.5V」となります.したがって正解は(d)の0.5Vということになります.
●コンデンサを並列接続したときの合成容量
コンデンサの容量値は,電極の面積に比例します.コンデンサを並列接続した場合,電極の面積はそれぞれのコンデンサの面積の和になります.そのため,図2のように,コンデンサを並列接続したときの合成容量値(C)はそれぞれの容量値の和になることが,直観的に分かります.
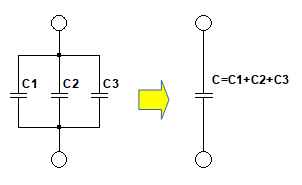
合成容量値はそれぞれのコンデンサの容量の和になる.
念のため,コンデンサを並列接続したときの合成容量の値を,数式を使って確認します.図2のように並列接続されている場合,C1,C2,C3の両端電圧は同じになります.ここで,3つのコンデンサの両端電圧をVとすると,それぞれのコンデンサに蓄えられている電荷(Q1,Q2,Q3)は「Q1=V*C1,Q2=V*C2,Q3=V*C3」と表せます.合成コンデンサ(C)の電荷(Q)は,これらの電荷をすべて足し合わせたものなり,両端電圧はVとなります.そのため合成容量は式1のようにしそれぞれの容量値の和となります.
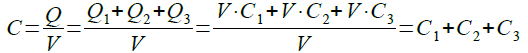 ・・・・・・・(1)
・・・・・・・(1)
●コンデンサを直列接続したときの合成容量
コンデンサを直列接続した場合の合成容量の値は,直観的には分かりにくいかもしれません.そこで,図3のように3つのコンデンサを直列に接続し,一定電流で充電した場合,端子電圧がどのようになるかを計算して,合成容量を求めてみます.
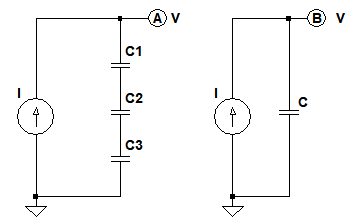
C1,C2,C3に蓄えられる電荷はすべて等しい.
図3の左において,C1,C2,C3は直列に接続されているため,電流源(I)でt秒間充電した場合に蓄えられる電荷(Q)はすべて等しくなります.そして,それぞれのコンデンサの両端電圧(V1,V2,V3)は「V1=Q/C1,V2=Q/C2,V3=Q/C3」となり,A点の電圧(V)はV1,V2,V3を足したものになります.また,図3の右でt秒間充電したときにCに蓄えられる電荷は,左図のそれぞれのコンデンサと同じくQになります.ここでB点の電圧が,図3の左のA点の電圧と同じだった場合,Cの値は,C1,C2,C3を直列接続した合成容量と同じであると考えることができます.これらを踏まえて式を解いていきます.まず,A点の電圧は式2で表すことができます.
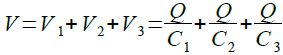 ・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・(2)
B点の電圧は,式3で表されます.
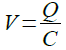 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
A点の電圧とB点の電圧が等しいとすると,式4が成立します.
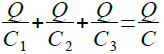 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4の両辺をQで割り,Cについて解くと,式5のように,コンデンサを直列接続した場合の合成容量を求める式が得られます.
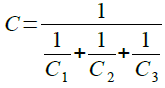 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
式5を図に表すと図4のようになります.
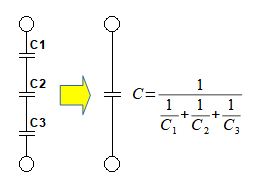
合成容量値はそれぞれのコンデンサの容量の逆数の和の逆数になる.
●コンデンサを並列と直列接続したときの充電特性をLTspiceで確認する
式1と式5の計算式を検証するため,コンデンサを並列と直列接続したときの充電特性を図5で確認してみます.
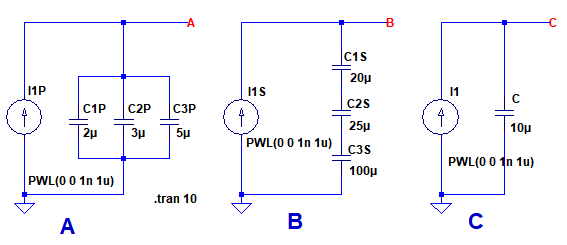
A,B,Cの回路の合成容量はいずれも10μFとなっている.
図5のAは,2μFと3μFおよび5μFが並列になっているため合成容量は式6のように10μFとなります.
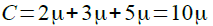 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
図5のBは,20μFと25μFおよび100μFが直列になっています.合成容量は式7のように10μFになります.
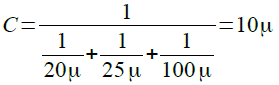 ・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・(7)
図5のCは,比較用の10μFのコンデンサです.それぞれのコンデンサには,0Aから1ns後に1μAにステップ状に変化する電流源が接続されています.この回路でA,B,C各ポイントの電圧がどのように変化するかをシミュレーションします.
図6は図5のシミュレーション結果です.A,B,Cそれぞれのポイントの電圧はまったく同じ傾きとなっていいます.これはAとBの合成容量値が,Cのコンデンサの容量値とまったく同じであることを表しています.
A,B,Cそれぞれのポイントの電圧はまったく同じ傾きとなっている
●並列接続と直列接続を組み合わせたときの充電特性をLTspiceで確認する
図1の回路は並列接続と直列接続を組み合わせたものです.そのため,この回路の合成容量は式1と式5を組み合わせ,式8のようにして2μFと計算することができます.
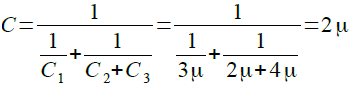 ・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・(8)
OUT端子のt秒後の電圧(VOUT)は充電電流をIとし,合成容量をCとすると「VOUT=I*t/C」で表されます.図1の数値を代入すると,1秒後の電圧は式9のように0.5Vになります.
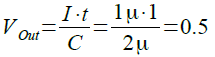 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
図7は,図1の回路をシミュレーションするための回路です.
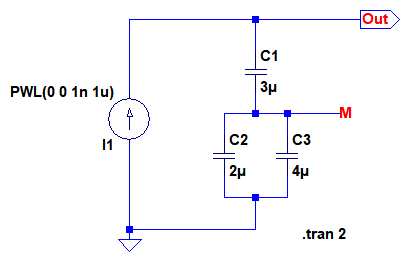
I1の電流を0Aから1ns後に1uAになるよう,ステップ状に変化させている.
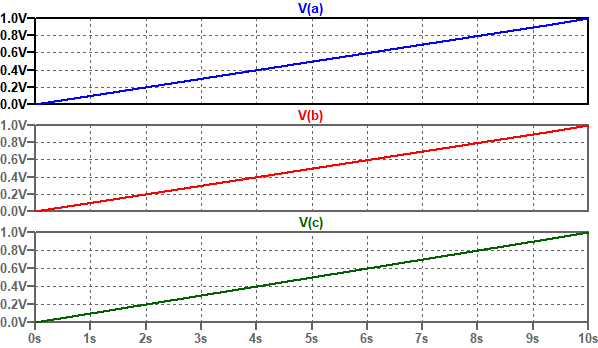
図8が図7の回路のシミュレーション結果です.式9で計算したように,1秒後の電圧は0.5Vになっていることが分かります.
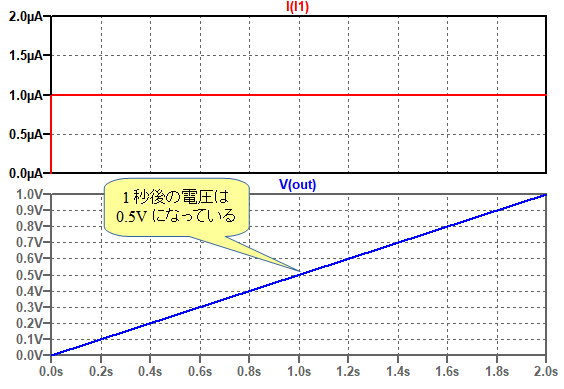
計算結果と同様に1秒後の電圧は0.5Vになっている.
このように,コンデンサを並列接続したり,直列接続することで,様々な容量値のコンデンサを合成することができます.電子工作で回路を試作するときなどに,必要な容量値のコンデンサがなくても,手持ちのコンデンサを並列接続したり直列接続することで,代替することができます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice5_011.zip
●データ・ファイル内容
Capacitor_P_S.asc:図5の回路
Capacitor_S_P.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










