電力伝送に見る交流信号の位相

図1のV1~V3は,ピーク電圧1Vで周期が12ms(周波数83.333Hz)の正弦波電圧を発生する電圧源です.V2はV1に対して4msの時間ずれがあり,V3はV1に対して8msの時間ずれがあります.それぞれの電圧源はR1~R3の1Ωの抵抗を介して接続されています.ここで,X点の電圧のピーク値は,(a)~(d)のどれでしょか.
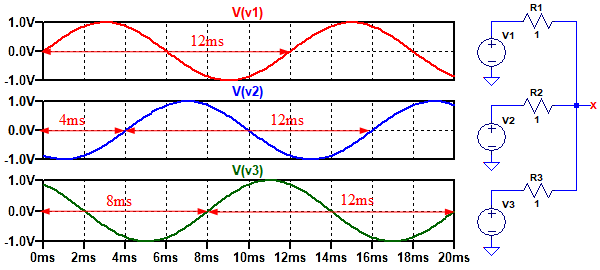
X点の電圧のピーク値はいくつ?
(a)0V (b)333.3mV (c)1V (d)3V
X点の電圧は,V1~V3の電圧を一定の比率で加算したものになります.数式を立てて考える場合は,それぞれの電圧をサイン波で表現して計算します.また,図1の各時間ごとの,それぞれの電圧を加算することでも,答えが分かります.
V1~V3の電圧をサイン波で表現し,加算した電圧(VX)は「VX=(sin(ωt)+sin(ωt-2π/3)+sin(ωt-4π/3))/3」となり,三角関数の公式を適用すると「VX=0」となります.また,図1の波形を見ると,0msのときの各電圧はV1が0V,V2とV3は同じ電圧で符号が逆になっています.そのため加算した電圧は0Vです.その他の時間も同様に調べると,0Vとなることが分かります.
●時間ずれと位相角度
位相は,周期的に変化する信号の位置を表すもので,通常は角度で表されます.正弦波信号は振幅をAとし,角周波数をω,初期位相をαとすると,A*sin(ωt+α)で表されます.
図1のV1の初期位相は0です.V2,V3はそれぞれ異なった初期位相となっていると考えることができます.図1では,V1とV2の時間ずれが4msとなっていますが,この時間ずれを角度で表したものが,位相ということになります.
時間ずれと角度の関係を理解するには,正弦波を等速円運動と考えると分かりやすくなります.図2は,正弦波を等速円運動と考えたときの模式図です.
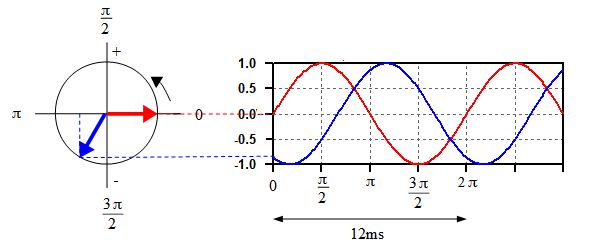
矢印のy軸の長さを縦軸,角度を横軸としてプロットしたものが右
図2左の円の中の赤い矢印は,初期位相が0です.青い矢印は,初期位相が-2π/3ラジアンとなっていることを表現しています.この二つの矢印が,同じ速度で反時計回りに回転したときの,矢印のy軸の長さを縦軸,角度を横軸としてプロットしたものが,図2右です.この図を見ると,初期位相の差が角度で表現されるということが分かると思います.
図1では,正弦波の一周期が12msとなっていました.図2の矢印が一周する(2π回転する)時間が12msということになります.4msの時間ずれは12msの1/3なので,角度に直すと2π/3となることが分かります.そのため,図1のV1は式1となります.
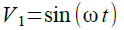 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
図1のV2は式2となります.
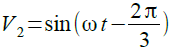 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
図1のV3は式3で表すことができます.
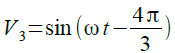 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
ここで,周期をTとし,ω=2π/Tとします.
●位相のずれた3つの信号の加算
式1~3を使用して図1のX点の波形がどのようなものになるか,計算します.図1の回路は,電圧源が3つあります.しかし,2つの電源は,0V(短絡)と考え,1つの電源によるX点の電圧を3通り計算した後,それらを足し合わせるという手法を使うことで,計算が簡単になります.
まず,V1について考えると,X点の電圧(VX1)は,V1を「R1」と「R2,R3を並列接続したもの」で分圧した値になります.抵抗はすべて1Ωなので「VX1=V1/3」となります.同様に「VX2=V2/3」,「VX3=V3/3」となります.VXはこれらをすべて足し合わせ「VX=VX1+VX2+VX3」で求めることができます.以上の結果と式1~式3とまとめると,VXは式4のようになります.
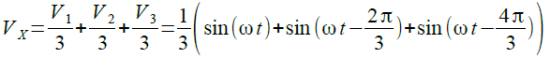 ・・・・・(4)
・・・・・(4)
式4を三角関数の公式(加法定理)を利用して変形していくと,式(5)のように0となることが分かります.
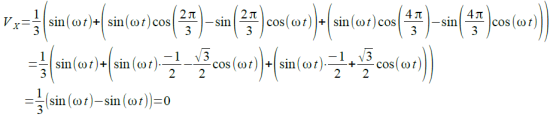 ・・・・・(5)
・・・・・(5)
式5のように2π/3ラジアン(120度)ずつ位相のずれた3つの正弦波を加算すると0になります.このような3つの正弦波を組み合わせた電源は三相交流と呼ばれ,電力を送電する方法として広く使用されています.
●位相のずれた3つの信号の加算をLTspiceで確認する
図3は,図1の回路をシミュレーションするための回路です.ビヘイビア電源を使用し,式1~3を使用して位相のずれた3つの正弦波を発生させています.
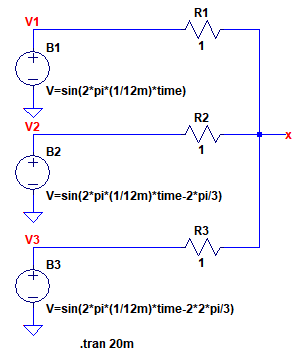
ビヘイビア電源を使用して,位相のずれた3つの正弦波を発生させる
図4は,図3のシミュレーション結果です.X端子の電圧は0Vとなっていることが分かります.
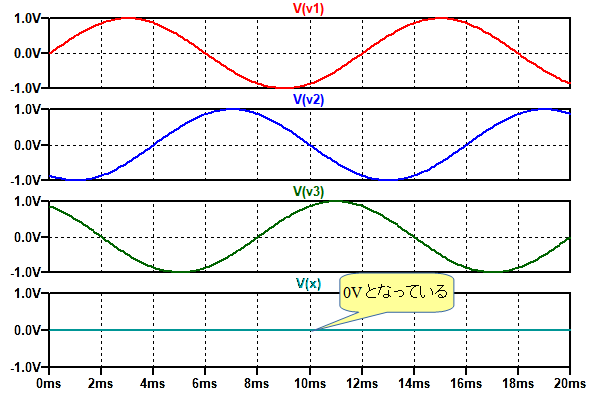
X点の電圧は0Vとなっていることが分かる.
●電力の送電に三相交流が使われる理由をシミュレーションで確認
2π/3ラジアン(120度)ずつ位相のずれた三相交流は,電力の送電に広く使用されています.図5は,電力の送電に三相交流が使われる理由をシミュレーションで確認するための回路です.図5のV4~V6は全て同じ位相となっており,V1~V3は2π/3ラジアンずつ位相がずれた電圧となっています.抵抗は電力を消費する負荷を想定したものです.
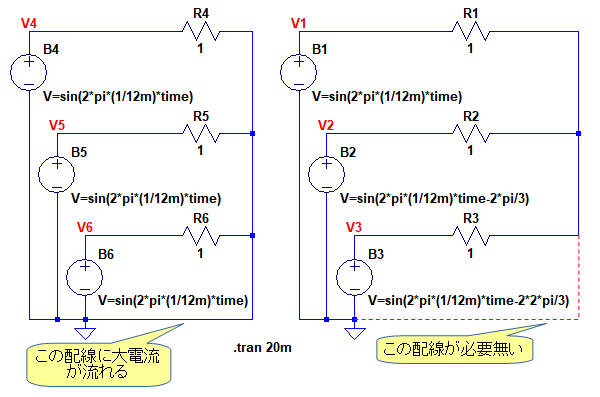
V4~V6は全て同じ位相で,V1~V3は2π/3ラジアンずつ位相がずれた電圧.
図6は,図5のシミュレーション結果です.R1とR4には同じ電流が流れており,R1とR4で発生する電力は同じです.また図6には表示していませんが,R2,R3,R5,R6で発生する電力も同じです.
V4~V6が全て同じ位相のため,R4~R6の電流を加算したものは,それぞれの抵抗に流れる電流の3倍の電流となっています.一方,V1~V3は2π/3ラジアンずつ位相がずれた電圧となっているため,R1~R3の電流を加算したものは,電流が0Aとなっています.そのため,図5左では電源と負荷を結ぶ配線が4本必要なのに対し,右図では3本で同じ電力を伝送できます.
このように,送電に必要な配線が少なくなるため,電力伝送には三相交流が使われています.
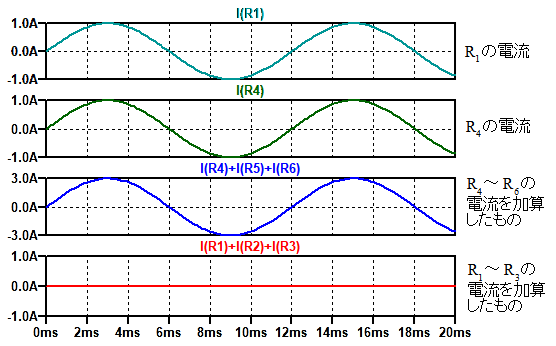
R1~R3の電流を加算したものは,電流が0Aとなっている.
以上,交流信号の位相について解説しました.今回は電力伝送を例にしましたが,電子回路設計を行うときも,位相は重要な要素となります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice5_007.zip
●データ・ファイル内容
Three_phase.asc:図3の回路
Three_phase2.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
(8) オームの法則から学ぶLTspiceアナログ回路入門アーカイブs










