バッファ付き位相シフト発振回路の発振条件

図1は,バッファ付き位相シフト発振回路です.R1,R2,U1で正帰還ループの反転アンプ構成し,U2とU3のOPアンプで,ゲインが1倍のユニティ・ゲイン・バッファ回路を構成しています.正帰還ループで,図1の回路を発振させる反転アンプのゲインは,(a)~(d)のどれでしょうか.なお,回路内のR3,R4,R5は同じ抵抗値,C1,C2,C3は同じ容量値,OPアンプは理想とします.
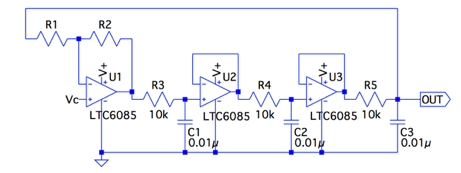
発振させるためには,反転アンプのゲインはいくらか.
(a)-1倍 (b)-3倍 (c)-4倍 (d)-8倍
正帰還を使った発振回路は,正帰還ループの1カ所を切断したとき,切断箇所から回路を一巡して戻ってくる信号が,「同じ振幅」で「位相差が無い」ことが発振条件となります.位相差が無い条件は,位相差360°でも同意です.図1において,位相差360°の内訳は,反転アンプで180°位相が変わり,「R3=R4=R5とC1=C2=C3」の条件より,残り180°を三等分して,1つのCR積分回路で60°の位相差となります.このときのCR積分回路で減衰するゲインを,反転アンプのゲインで補い,正帰還のループ・ゲインを1にします.
正帰還を利用した発振回路は,発振する条件として,正帰還ループの「ループ・ゲイン=1」,「位相差=360°」が必要です.図1のバッファ付き位相シフト発振回路は,正帰還ループの位相に着目すると,反転アンプで180°の位相差,1つの1次CR積分回路で60°の位相差ですので,三つ通過することにより180°の位相差となって,全体で360°の位相差になります.
次に,ループ・ゲインに着目します.図2は,図1の1つの1次CR積分回路を抜き出して,その周波数特性を調べた結果です.1次CR積分回路の位相が-60°になるときのゲインを調べると,「-6dB=1/2倍」となります.この1次CR積分回路を3つ通過した後のゲインは「(1/2)3=1/8」です.よって「ループ・ゲイン=1」とするには,反転アンプで8倍のゲインが必要となり,解答の(d)となります.
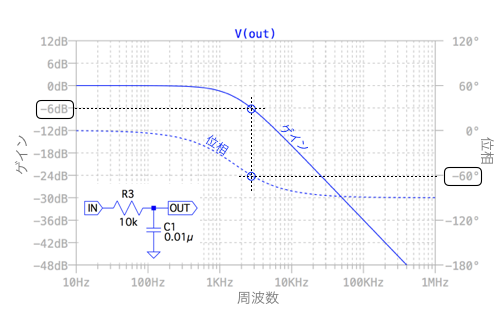
-60°の位相遅れのとき,ゲインは-6dBとなる.
●発振周波数と反転アンプに必要なゲインの導出
図3は,図1の「R3=R4=R5=R」,「C1=C2=C3=C」としたブロック図です.ゲインが1倍のバッファは,1次CR積分回路の負荷が,OPアンプの高い入力インピーダンスのみにするために使われています.この図を用いて,発振周波数と発振に必要な反転アンプのゲイン(G)を求めます.
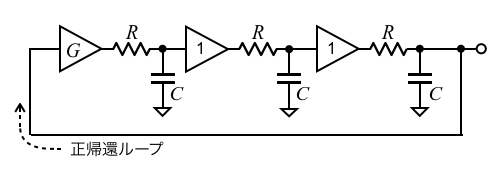
3つの抵抗と3つのコンデンサは同じ値.
まず,発振周波数を求めます.発振させるための条件「ループ・ゲイン=1」より,図3から式1が求まります.
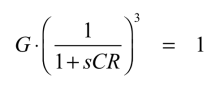 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
式1のラプラス演算子(s)を「s=jω」とし,整理すると式2となります.
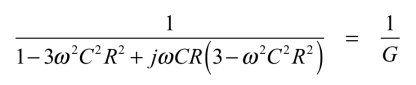 ・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・(2)
式2の分母中の複素数の項をゼロにするには,式3となります.
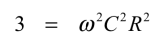 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3より,発振時の角周波数をω0とすれば,式4となります.
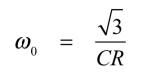 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4より,「ω=2πf」とすれば,発振周波数は式5となります.
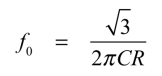 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
次に,発振させるための反転アンプのゲインを求めます.式4を式2へ代入すれば,式6となります.
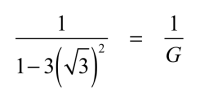 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
式6より,反転アンプのゲイン(G)は式7となり,解答の(d)となります.
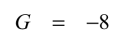 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
●発振周波数における1次CR積分回路のゲインと位相
図3にある3つの1次CR積分回路のうち,1つの積分回路について,発振周波数におけるゲインと位相が図2となるか計算で確認します.1次CR積分回路の伝達関数は,式8となります.
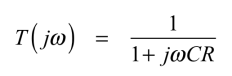 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式8へ式4の発振周波数を代入すると,式9となります.
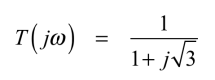 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
式9のゲインを求めると,式10となります.
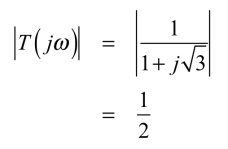 ・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
式9の位相を求めると,式11となります.
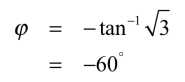 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
式10,式11より,発振しているときの1次CR積分回路は,「ゲイン=1/2」で,「位相差=-60°」であり,図2の関係であることが,計算でも確かめました.
●LTspiceでバッファ付き位相シフト発振回路を確認する
図4は,図1のOPアンプを,CMOSのクワッドOPアンプ(1つのパッケージに4つのOPアンプが封入されている)を使い,OUT端子に出力バッファを加えた回路です.1次CR積分回路の定数は「R3=R4=R5=10kΩ」,「C1=C2=C3=0.01μF」です.また,反転アンプのゲインは,OPアンプが理想であれば,式7の8倍のゲインですが,実際は理想ではないため,ここでは「-R2/R1=-9倍」としました.式5を用いると,図4の発振周波数は「f0=2.76kHz」となります.シミュレーションは,0s~110ms間を過渡解析し,OUT端子の波形をプロットします.
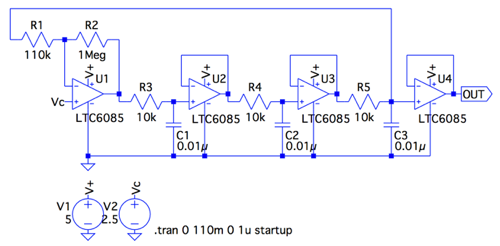
クワッドOPアンプを使い,出力にはバッファ回路を入れている.
図5は,図4のシミュレーション結果です.OUT端子の波形は正弦波の発振出力で,波形の周期より,発振周波数は「f0=2.78kHz」です.計算値の「f0=2.76kHz」と近い値となります.
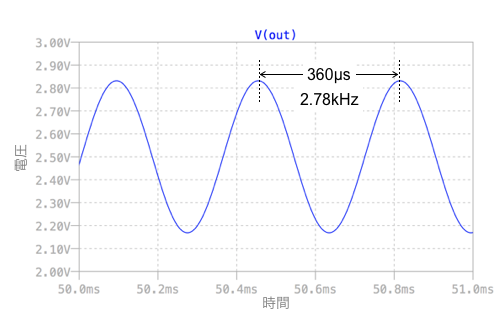
過渡解析での発振波形.
図6は,図5の波形が安定した10ms~110ms間のFFT結果です.基本波の周波数は2.78kHzで,高調波歪みが少ない正弦波発振であることがわかります.
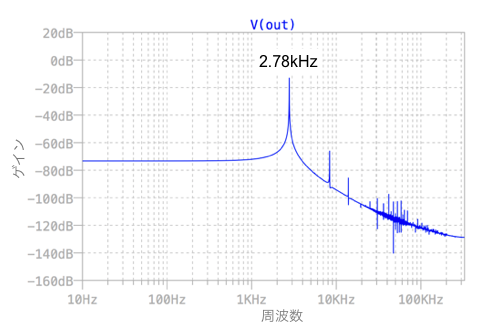
高調波歪みが少ない正弦波発振回路であることが分かる.
以上,解説したように,バッファ付き位相シフト発振回路は,3つある1次CR積分回路の間にOPアンプを入れることにより,互いの干渉を無くした正弦波発振回路です.クワッドOPアンプを使えば,残りの1つのOPアンプで,出力バッファも構成でき,低インピーダンスで後段の回路を駆動できます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_046.zip
●データ・ファイル内容
Buffered_Phase_Shift_Oscillator.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs










