3つの機能を有するフィルタの特性

■問題
アナログ回路の基礎 ― 中級

平賀　公久　Kimihisa Hiraga

　図1は，LPF(Low Pass Filter)，BPF(Band Pass Filter)，HPF(High Pass Filter)の3つのフィルタリング機能を出力する状態変数形フィルタ(State variable filter)のブロック線図です．図1は，1つの入力端子(v_i)に対し,3つの出力端子(v_o1，v_o2，v_o3)があり，それぞれ違うフィルタリング機能を出力します．図1において，v_o1，v_o2，v_o3のフィルタリング機能の正しい組み合わせは，次の(a)～(d)のどれでしょうか．

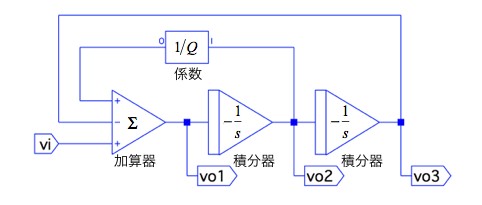
図1　3つのフィルタリング機能を有する状態変数形フィルタのブロック線図
ブロック線図は演算要素の記号で表している．

(a)　v_o1：LPF，v_o2：BPF，v_o3：HPF
(b)　v_o1：HPF，v_o2：BPF，v_o3：LPF
(c)　v_o1：LPF，v_o2：HPF，v_o3：BPF
(d)　v_o1：HPF，v_o2：LPF，v_o3：BPF

■ヒント

　図1のブロック線図は，演算要素の記号で表しており，加算器は入力側にあるプラスとマイナスの関係で加算されて出力します．積分器は「-1/s」のラプラス演算子で表した理想積分器です．係数「1/Q」はこのブロックを通過すると，「1/Q」の係数を乗ずることになります．よって，加算器の出力であるv_o1は式1となります．

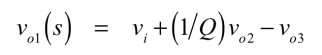・・・・・・・・・・・・・・・・・・・・・(1)

　式1を用い，積分器を通過した後のv_o1(s)，v_o2(s)，v_o3(s)の伝達関数を求め，3つのフィルタリング機能の伝達関数の一般式と比較すると分かります．ここで，3つのフィルタリング機能(LPF，BPF，HPF)の伝達関数は，

式2がLPFの伝達関数です．

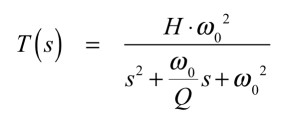・・・・・・・・・・・・・・・・・・・・・・・(2)

式3がBPFの伝達関数です．

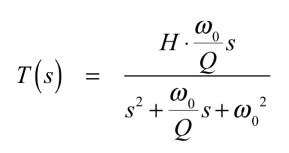・・・・・・・・・・・・・・・・・・・・・・・(3)

式4がHPFの伝達関数です．

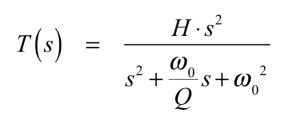・・・・・・・・・・・・・・・・・・・・・・・(4)

　ただし，式2から式4で，Hはフィルタ特性のゲインに相当します．ω₀はLPFとHPFのときがコーナ周波数で，BPFのときが中心周波数です．Qはフィルタのクオリティ・ファクタを表しています．

■解答

(b)　v_o1：HPF，v_o2：BPF，v_o3：LPF

　図1の積分器を通過した後のv_o2は，式5となります．

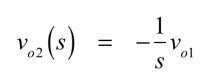・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　同様に，v_o3は式6となります．

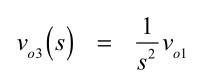・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式5と式6を，加算器出力の式1へ代入すると「v_o1(s)/v_i(s)」の伝達関数が得られ，式7となります．

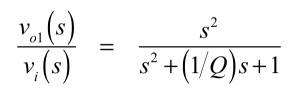・・・・・・・・・・・・・・・・・・・・・・(7)

　「v_o2(s)/v_i(s)」の伝達関数は，式7が1つの積分器を通過した後なので，式8となります．

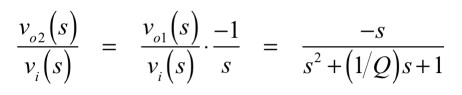・・・・・・・・・・・(8)

　同様に，「v_o3(s)/v_i(s)」の伝達関数は，式7が2つの積分器を通過した後なので，式9となります．

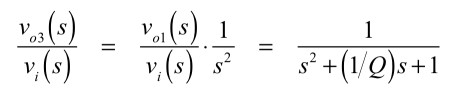・・・・・・・・・・・(9)

　ここで，式7，式8，式9と，ヒントで示した3つのフィルタリング機能の伝達関数の式2，式3，式4を比較します．式2，式3，式4の違いは，分子のラプラス演算子「s」にあります．LPFの伝達関数式2の分子には「s」がありません．また，BPFの伝達関数式3は「s」があります．HPFの伝達関数式4は「s²」です．この違いでフィルタの機能が分類できます．以上より，式7がHPF，式8がBPF，式9がLPFとなり，解答は(b)となります．

■解説

●状態変数形フィルタの概要
　状態変数形フィルタは，考案者3人の名前(Kerwin，Huelsman，Newcomb)の名前を取り，KHN State variable filterとも呼ばれています．回路の構造は，状態方程式を微分方程式で実現する手法であり，アナログ・コンピュータのプログラミングによく似ています．
　状態変数形フィルタは，OPアンプを1つ使った2次アクティブ・フィルタと比べると次の利点があります．ゲインとクオリティ・ファクタは，コーナ周波数や中心周波数に関係なく調整できます．また，抵抗やコンデンサの変化に対するゲインの感度が低いです．さらに，同一の回路から3つのフィルタリング機能を出力できます．
　ここでは，状態変数形フィルタのブロック線図を，電圧制御電流源を使った加算器と積分器で表し，3つのフィルタリング機能をシミュレーションで確かめ，OPアンプを使った実回路まで解説します．

●ブロック線図をシミュレーションする
　図1の状態変数形フィルタのブロック線図は，加算器，積分器，係数で表しています．これらの各ブロックは，サブサーキットとし，図2に示す電圧制御電圧源で表しました．図2(a)が加算器で，プラスとマイナスの方向は，電圧制御電圧源のゲインで「1」または「-1」で表しています．図2(b)が積分器で，ラプラス演算子「Laplace=-1/s」で表しています．図2(c)が係数で，「1/Q=1.414」としました．これは「Q=0.707=1/√2」であり，フィルタの特性はバタワース特性となります．

図2　図1の加算器，積分器，係数をサブサーキットで表した
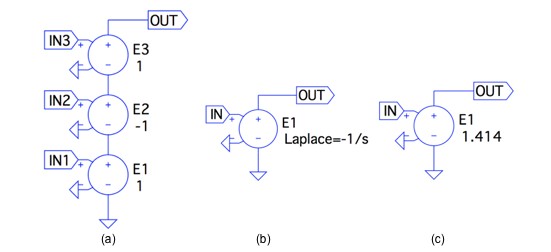
(a)加算器，(b)積分器，(c)係数の回路

　図3は，図1をシミュレーションする回路で，3つのフィルタリング機能の周波数特性を確かめるためにAC解析します．

図3　図1の状態変数形フィルタをシミュレーションする回路

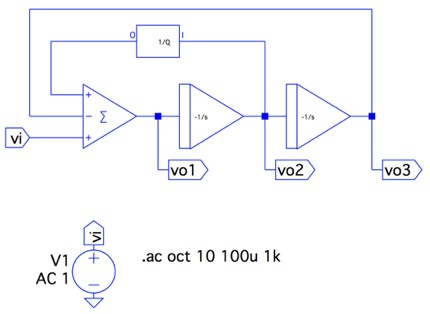
　図4は，その結果で，v_o1，v_o2，v_o3をプロットしました．解答で示した通り，v_o1がHPF，v_o2がBPF，v_o3がLPFであることが確認できます．また，ω₀は，式7，式8，式9とフィルタリング機能の伝達関数である式2，式3，式4を比較すれば，「ω₀=1rad/s」となります．なので，HPFのゲインは「ω=∞」のとき0dB(1倍)で，BPFのゲインは「ω=ω₀」のとき-3dB(0.707倍)で，LPFのゲインは「ω=0」のとき0dB(1倍)となり，計算式とシミュレーションが一致していることが分かります．

図4　図3のシミュレーション結果
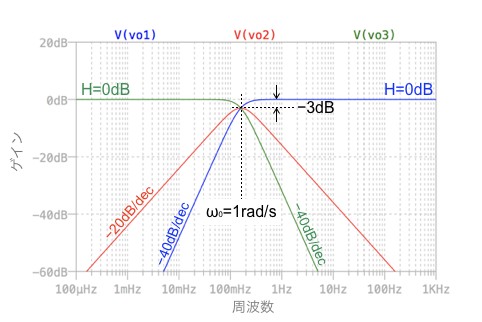
v_o1はHPF，v_o2はBPF，v_o3はLPFのフィルタリング機能となる．

●OPアンプを使った状態変数形フィルタ
　図1の状態変数形フィルタを実装するため，OPアンプを使った図5(a)の加減算回路と図5(b)の積分回路を用います．

図5　状態変数形フィルタで使う演算要素ブロックの実回路
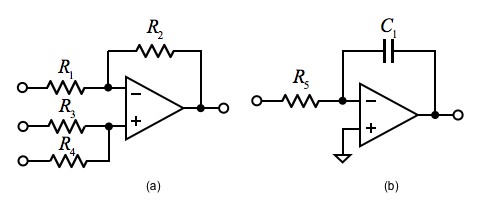
(a)OPアンプを使った加減算回路　(b)OPアンプを使った積分回路

　図6は，図1の状態変数形フィルタのブロック線図に従い，図5の(a)加減算回路と(b)積分回路で実装した回路です．

図6　状態変数形フィルタのブロック線図を実装した回路
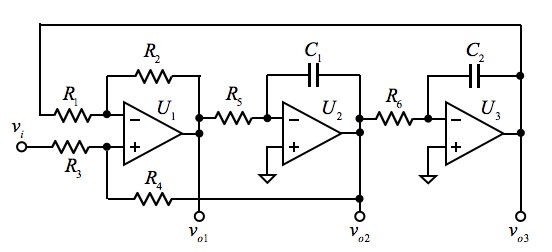
HPF出力 (v_o1)，BPF出力(v_o2)，LPF出力(v_o3)の3つのフィルタリング出力が得られる．

　図6の回路の伝達関数を計算し，v_o1，v_o2，v_o3のフィルタリング機能について調べます．v_o3とv_o2の関係は式10となります．

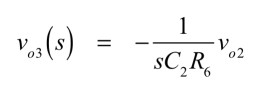・・・・・・・・・・・・・・・・・・・・・・・・(10)

　同様に，v_o2とv_o1の関係は式11となります．

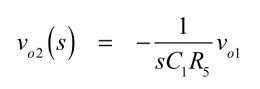・・・・・・・・・・・・・・・・・・・・・・・・(11)

　v_o1は，v_i，v_o2，v_o3の加減算であり，式12となります．

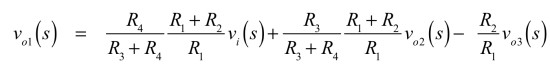・・・・・(12)

　式12へ，式10と式11を代入し，v_o3までの伝達関数を求めると，式13となります．これはLPFの伝達関数です．

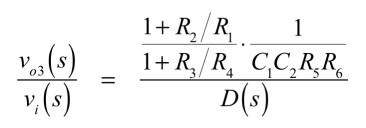・・・・・・・・・・・・・・・・・(13)

　ここで，D(s)は式14となり，以降のD(s)もこの式となります．

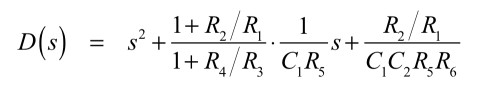・・・・・・・・・(14)

　v_o2までの伝達関数は，式13と式10より，式15となります．これはBPFの伝達関数です．

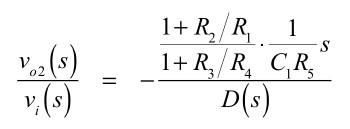・・・・・・・・・・・・・・・・・・(15)

　v_o1までの伝達関数は，式15と式11より式16となります．これはHPFの伝達関数です．

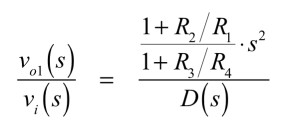・・・・・・・・・・・・・・・・・・・・・(16)

　これより，図6のフィルタリング機能は，図1のブロック線図で示したものと同じであることが分かります．

●フィルタの H，ω₀，Qの導出
　フィルタのH（ゲインに相当）やω₀（コーナ周波数と中心周波数），Q(クオリティ・ファクタ)について求めます．式14のD(s)は，式13，式15，式16の共通の分母です．これよりω₀が求まり，式17となります．

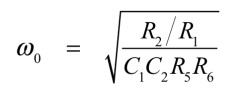・・・・・・・・・・・・・・・・・・・・・・・・・・(17)

　同様に，フィルタのQは式18となります．

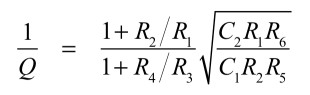・・・・・・・・・・・・・・・・・・・・・(18)

　「ω=0」のとき，v_o3(LPF)のゲインは，式13と式2を比較して式19となります．

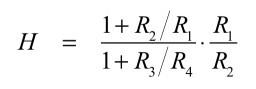・・・・・・・・・・・・・・・・・・・・・・・・(19)

　「ω=ω₀」のとき，v_o2(BPF)のゲインは，式15と式3を比較して式20となります．マイナスは位相が反転することを表しています．

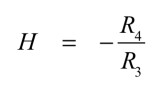・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(20)

　「ω=∞」のとき，v_o1(HPF)のゲインは，式16と式4を比較して式21となります．

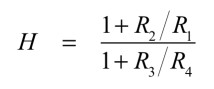・・・・・・・・・・・・・・・・・・・・・・・・・・・(21)

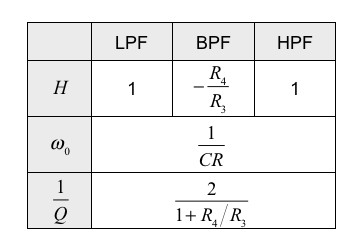
　状態変数形フィルタのH，ω₀，Qは「R₁=R₂」,「R₅=R₆=R」,「C₁=C₂=C」とすれば，表1のように簡単になります．

表1　フィルタ特性の違いによる，ゲイン(H)，周波数(ω₀)，Qの関係

●OPアンプを使った状態変数形フィルタのシミュレーション
　図7は，状態変数形フィルタをシミュレーションする回路です．

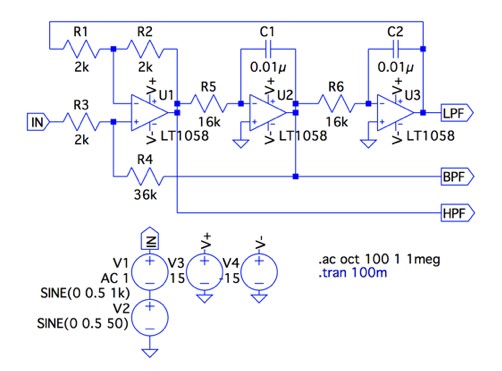
図7　状態変数形フィルタをシミュレーションする回路回路定数は中心周波数が1kHz，ゲインが25.2dB，Q=9.5のBPFとなるように設定．

　抵抗とコンデンサは，「R₁=R₂」,「R₅=R₆=R」,「C₁=C₂=C」とします．表1より，この状態変数形フィルタは，R₃とR₄の抵抗比により，増幅機能があるBPFとして働きます．
　回路定数は表1を用いて，ゲインを式22で設定しました．

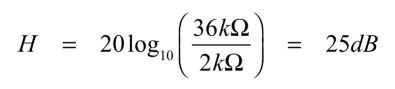・・・・・・・・・・・・・・・(22)

　中心周波数は，式23で設定しました．

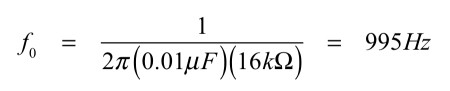・・・・・・・・・・・(23)

　Qは，式24でBPFとなるように設定しました．

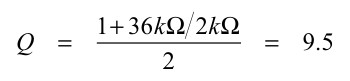・・・・・・・・・・・・・・・・・・(24)

　図8がAC解析によるBPFの周波数特性です．ゲイン,中心周波数,Qとも設定とおりの値となります．グラフが見にくくなるため，LPFとHPFはプロットしませんでしたが，この2つの出力はコーナ周波数でピークを持つLPFとHPFになります．

図8　図7のAC解析によるBPFの周波数特性
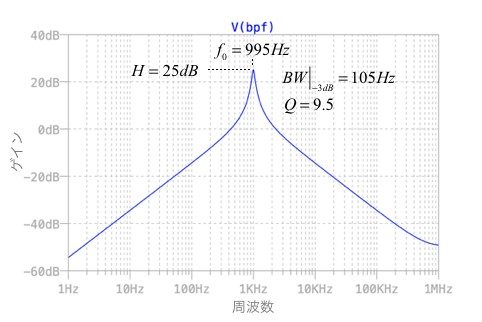
回路定数で設定したフィルタ特性となる．

　図9は，図7の入力に，0.5Vの振幅で1kHzの正弦波信号と同じ0.5Vの振幅で，50Hzの正弦波を重畳して雑音と見立てたシミュレーション結果です．解析指定は「.tran 100m」の過渡解析に変更しました．V(in)が入力波形で，大きなうねりが50Hz，小さな振動が1kHzです．状態変数形フィルタのBPF出力をみると，50Hzの雑音は抑圧し，1kHzの信号を増幅して出力することが分かります．

図9　図7の過渡解析結果
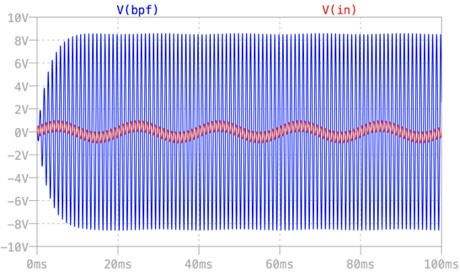
50Hzの信号は抑圧し，1kHzの信号が増幅され出力される．

　以上，解説したように状態変数形フィルタは，1つの回路で3つのフィルタリング機能があります．3つの出力は，フィルタのビルディング・ブロックとして利用でき，OPアンプを1つ追加したバイクアッド・フィルタ(Biquad filter)などでも使われています．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice4_035.zip

●データ・ファイル内容
State_variable_filter_Block_diagram.asc：図3の回路
State_variable_filter.asc：図7の回路
Summer.asc：図3の加算器のサブサーキット
Summer.asy：図3の加算器のシンボル
Integrator.asc：図3の積分器のサブサーキット
Integrator.asy：図3の積分器のシンボル
Reciprocal_Q.asc：図3の係数のサブサーキット
Reciprocal_Q.asy：図3の係数のシンボル