負帰還によるひずみ改善効果
図1は，負帰還によりひずみが改善されることを検証するためのOPアンプを使用した回路です．入力信号として1kHzで2VPPの正弦波が加えられています．(A)～(D)の中で出力(Out)が入力と同じ正弦波となるものを全て答えてください．
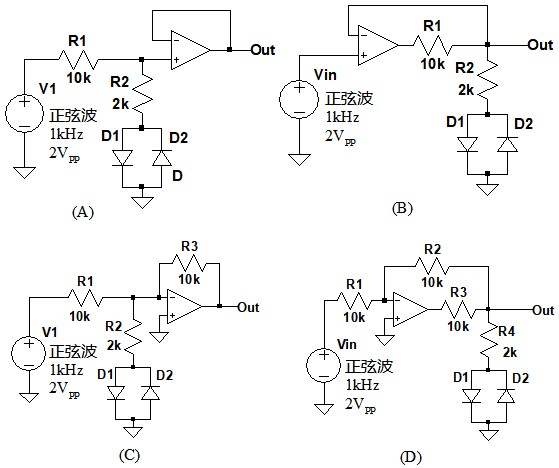
出力(Out)が入力と同じ正弦波となるものはどれ？
ダイオードD1とD2は，クリップ回路として動作します．信号振幅が0.7Vを越えると振幅を制限します．一方，負帰還にはひずみを改善する働きがあります．負帰還により，ひずみが改善されない回路はどれかを考えれば，解答が分かります．
回路(A)はOPアンプの入力部にクリップ回路が接続されているため，入力段で波形がひずみ，それがそのまま出力されます．回路(B)と(D)は，クリップ回路が負帰還ループ内にあるため，クリップ回路によるひずみは出力には現れません．回路(C)は，負帰還の効果によりOPアンプの反転入力端子の信号が非常に小さくなります．そのため，クリップ回路が動作せず，出力波形のひずみはありません．つまり，出力が入力と同じ正弦波となるのは，(A)を除いた(B)，(C)，(D)です．
●4つの回路の出力波形をシミュレーションする
まず，図1の(A)～(D)の回路に，入力信号として1kHzで2VPPの正弦波を加えたときの出力波形を確認してみます．図2は，図1の4つの回路の出力波形をシミュレーションする回路です．
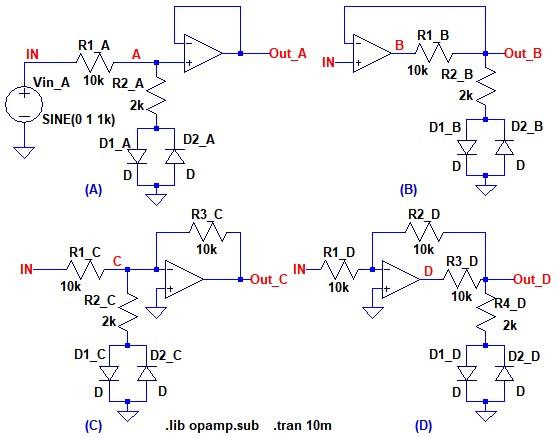
入力信号として1kHzで2VPPの正弦波を加えている．
図3は，図2のシュミレーション結果です．回路(A)の出力(Out_A)は波形がひずんでおり，正弦波ではありません．しかし，他の3つの回路の出力は入力と同じ正弦波となっています．回路(A)は，信号が小さいときダイオード(D1，D2)が導通しないため，入力信号は，そのままA点に伝わります．入力信号の振幅が0.7Vを越えるとダイオードが導通し，入力信号は抵抗R1とR2で分圧され振幅が制限されます．そのため，正弦波が変形してひずんだ波形になります．
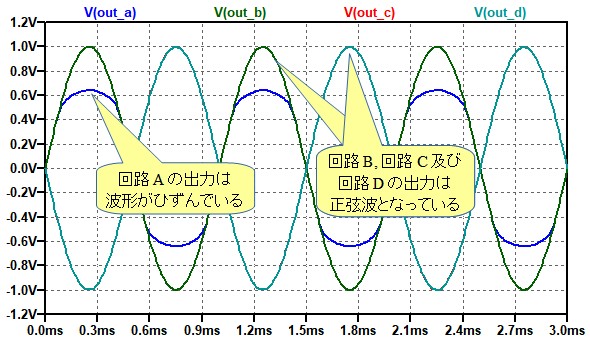
回路(A)の出力(Out_A)は波形がひずんでおり，正弦波ではない．
図4は，図2の回路(C)の入力(IN)と出力(Out_C)およびC点の波形です．回路(C)は反転アンプとなっているため，OPアンプの反転入力端子であるC点の波形は非常に小さくなっています．そのため，ダイオード(D1_C，D2_C)は導通せず，出力波形はひずみません．
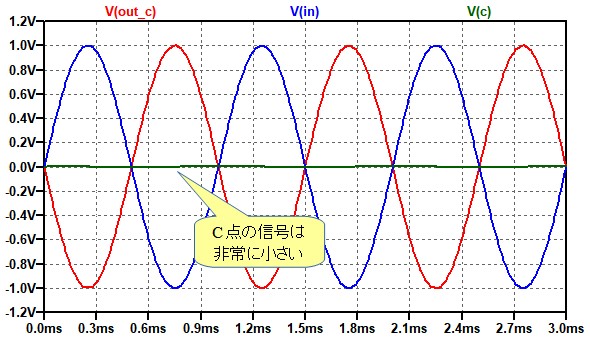
C点の波形は非常に小さいため，ダイオードは導通しない．
このように回路(C)はクリップ回路が動作しないため，波形ひずみが発生しません．回路(B)と(D)は，クリップ回路が動作しています．それでも，出力波形が正弦波となるのは，負帰還によりひずみが改善されるからです．そこで，負帰還により改善されるひずみの量は，どのように決まるのかを考えてみます．
●負帰還によるひずみの改善量を計算する
図5は，波形がひずんでいる回路(A)の出力をFFT解析したものです．ひずみ波形は基本波の1kHzに，3kHzや5kHzの高調波が加算されたものであることが分かります．
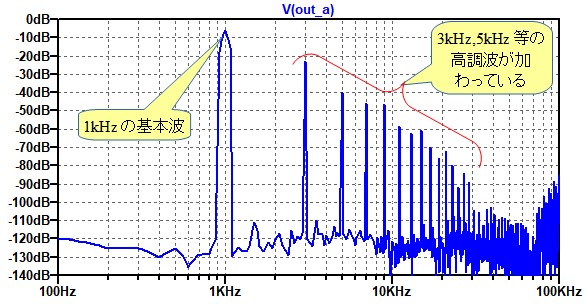
基本波に3kHzや5kHzの高調波が加算されている．
負帰還により，この高調波の量がどの程度減少するかを計算すれば，負帰還によるひずみの改善量が分かります．図6は，負帰還によるひずみの改善量を計算するための回路図です．OPアンプのオープン・ループゲインをAとし，帰還回路の帰還率をβとします．また，ひずみの高調波成分として，Vdという信号がOPアンプの出力に加算されています．負帰還により，このvdがどの程度小さくなるのかを計算します．
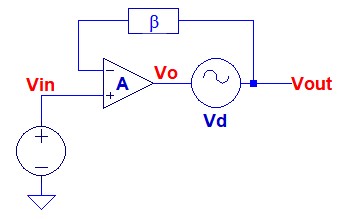
ひずみの高調波成分として，VdがOPアンプの出力に加算されている．
図6において，OPアンプ出力(VO)は，非反転入力端子の電圧と反転入力端子の電圧の差をA倍したものなので，式1で表されます．
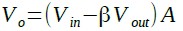・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また，出力(Vout)はOPアンプ出力に高調波のVdを足したものなので，式2になります．
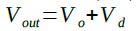・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式1，式2をVoutについて解くと，式3になります．
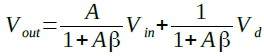・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3の第一項は帰還アンプのゲインの一般式です．帰還アンプのゲインをGとし，OPアンプのゲインAが十分大きいとすると，Gは式4であらわされます．
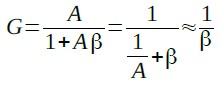・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式3をGを使用して書き直すと式5になります．
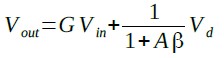・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
式5より，ひずみの高調波成分Vdは1/(1+Aβ)に減少することが分かります．OPアンプのオープン・ループ利得(A)および帰還率(β)が大きいほど，高調波成分が小さくなり，ひずみ率が小さくなります．
●ひずみを改善しているときのOPアンプの出力波形
ダイオード・クリッパーが動作していても，出力波形が正弦波になっているとき，OPアンプの出力波形はどのような波形になっているでしょうか．図7は，図2の回路(B)と(D)の出力(Out_B，Out_D)およびB点，D点の波形です．B点，D点はOPアンプの出力です．
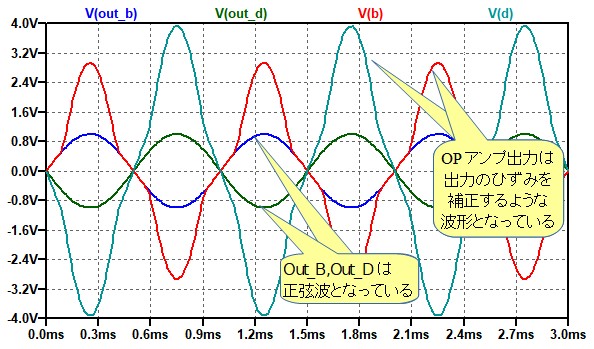
OPアンプ出力(B点，D点)は出力のひずみを補正する波形になっている．
出力波形は，負帰還の働きで正弦波となっています．このとき，OPアンプ出力であるB点，D点の波形は，「Out_B」と「Out_D」よりも振幅が大きく，正弦波とは異なる波形となっています．「Out_B」と「Out_D」の電圧が0.7Vよりも大きくなると，ダイオードが導通して出力振幅は，小さくなろうと振幅減少します．しかし，負帰還の働きにより，OPアンプ出力は，振幅減少を補うような波形になります．なお，D点の振幅がB点よりも大きくなっていますが，これは，回路(D)が反転アンプのため，帰還抵抗(R2_D)の電流がR3_Dに流れるからです．
以上，負帰還によるひずみ低減効果について解説しました．負帰還はアンプの出力段で発生するひずみを効果的に低減します．しかし，B級出力回路で発生するスイッチングによるひずみのようなものに対しては，OPアンプの帯域とスルーレートの制約から低減効果が低くなります．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice4_034.zip
●データ・ファイル内容
NFB_THD.asc：図2の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源＆アナログ回路入門・アーカイブs
