ジャイレータによる等価インダクタの実現

図1は,理想的なジャイレータを使ったインピーダンス変換回路です.v2側にコンデンサを接続すると,v1側からみた入力インピーダンス(zi)は,誘導性となりインダクタ(コイル)となります.回路のGは電圧制御電流源のコンダクタンスです.図1において,v1側からみた等価インダクタの値として正しいのは次の(a)~(d)のどれでしょうか.
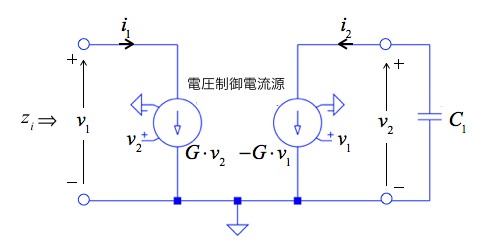
v2側にコンデンサをつけるとv1側からみた入力インピーダンスはインダクタにみえる.
(a) G倍したC1 (b) G2倍したC1 (c) 1/G倍したC1 (d) 1/G2倍したC1
理想ジャイレータは,2つの電圧制御電流源で表すことができます.図1の左側の電流源は,v2により制御した電流「i1=Gv2」が流れ,左側はv1により制御した「i2=-Gv1」が流れます.これを用いてC1を接続したときの入力インピーダンス「v1/i1」を求めると簡単にわかります.
図1の左側の電圧制御電流源から流れる電流は,i1であり式1となります.
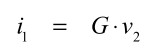 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
同様に,図1の右側の電圧制御電流源から流れる電流は,i2であり式2となります.
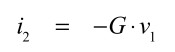 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
v2側にコンデンサ(C1)を接続するとv2の電圧は,式3となります.
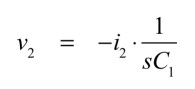 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
i1の電流は,式1と式3より式4となります.
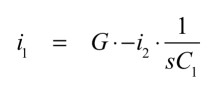 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
入力インピーダンスは,式4へ式2を代入し整理すると式5となります.
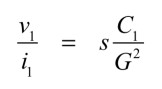 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
式5より,入力インピーダンスは,1/G2倍したC1となり解答の(d)となります.
●理想ジャイレータについて
ジャイレータは,インピーダンス変換回路として使われ,小さなコンデンサで等価的に大きなインダクタンスを得る回路トポロジです.ここでは理想ジャイレータの特性と,OPアンプでジャイレータを構成した具体例を解説します.
理想ジャイレータは,アドミタンス(yパラメータ)で表すと図2(a)の等価回路となります.回路記号は,図2(b)を用います.
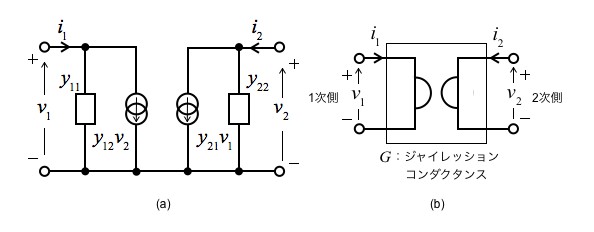
(a) yパラメータで表した等価回路
(b) ジャイレータの記号
図1と図2(a)を比べると「y12=G」,「y21=-G」であり,Gのことをジャイレッション・コンダクタンスと呼びます.y11とy22は1次側(v1側)と2次側(v2側)からみた各々のポートの入力アドミタンスであり,図1は,電流源の無限大のインピーダンスが見えます.そのため,アドミタンスは,インピーダンスの逆数ですから「y11=y22=0」となります.解答で計算した通り,ジャイレータに流れ込む1次側と2次側の電流は式1と式2なので理想ジャイレータをアドミタンス行列で表すと式6になります.
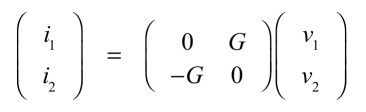 ・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・(6)
●理想ジャイレータの2つの特徴
式6の理想ジャイレータには2つの特徴があります.1つ目は,図3(a)の理想ジャイレータの2次側へ電圧を印加したとき,図3(b)のように1次側の電流は2次側の電圧で制御した電圧制御電流源となります.この関係は解答の式1に示しました.同様に,一次側に電圧を印加したときは,2次側の電流の向きが変わった電圧制御電圧源となります.
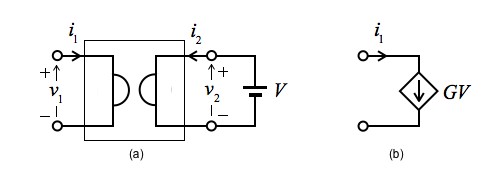
(a) ジャイレータの2次側に電圧を印加した回路
(b) (a)の1次側は2次側の電圧で制御した電圧制御電流源となる
2つ目の特徴は,1次側からみた入力インピーダンスが2次側に接続したインピーダンスの逆数になります.図4を用いて解説すると,1次側からみた入力インピーダンスは,コンデンサ周波数特性の逆の特性,つまり等価インダクタになり,2次側のコンデンサの値を1/G2倍したものとなります.この関係は解答の式5で示しました.
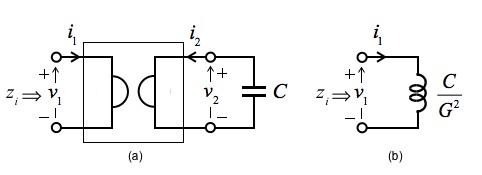
(a) ジャイレータの2次側にコンデンサを接続した回路
(b) (a)の1次側からみた入力インピーダンスは,等価インダクタとなる
●入力インピーダンスをLTspiceで確認する
図5(a)は,図1の1次側からみた,理想ジャイレータの入力インピーダンスをシミュレーションする回路です.図5(b)はインダクタ(L1)の値を,式5で得られた「C1/G2」で与え,図5(a)と比べます.ここで,図5(a)のジャイレッション・コンダクタンスは「G=1mA/V」,2次側のコンデンサは「C1=0.1μF」としました.図5(b)の変数Lは,「1/G=1kΩ」ですので,「L=(0.1μF)×(1kΩ2)」とし,「.params」中で計算し与えています.この計算は100mHのインダクタに相当します.
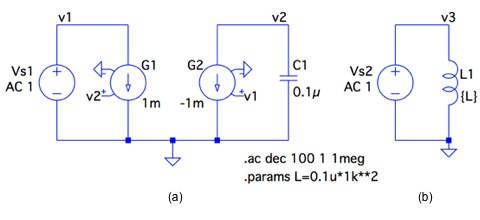
(a) 図1のGを1mA/V,C1を0.1μFとした回路
(b) 図1の計算値と同等なインダクタ
図6は,図5のシミュレーション結果です.図5(a)の1次側からみた入力インピーダンス 「v(v1)/I(G1)」と,図5(b)のインピーダンス 「v(v3)/I(L1)」をプロットしました.2つのプロットは重なっており,2次側につけた0.1μFのコンデンサは,1次側からみると100mHの等価インダクタとなっていることが分かります.
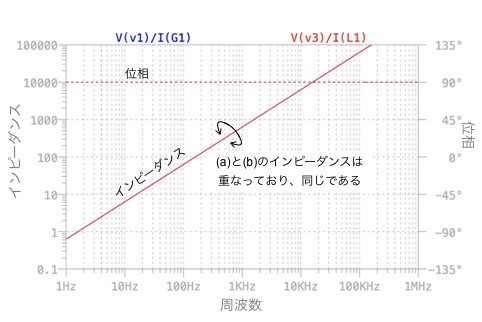
(a)と(b)は重なっており,計算で求めたインダクタンスが得られることが分かる.
●OPアンプを使ったジャイレータ回路
図7は,2つのOPアンプと抵抗を使ったジャイレータです.7つの抵抗は,全て同じ抵抗値「R1=R2=R3=R4=R5=R6=R7=R」とします.
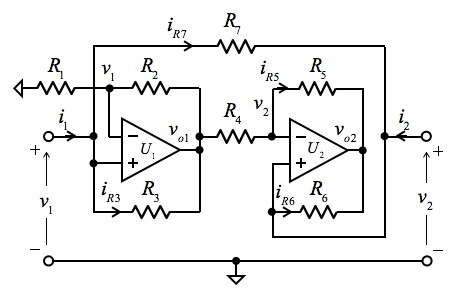
図7のジャイレータに流れ込む電流(i1,i2)を計算し,理想ジャイレータの式6と同じになるか確かめます.図7の回路記号を用いて回路方程式をたてると次のようになります.
i1の電流はKCLより式7となります.
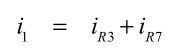 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7中のiR3は式8となります.
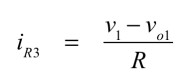 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式8中のvo1は,非反転アンプの出力ですので,式9となります.
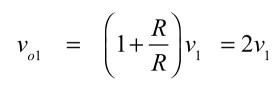 ・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・(9)
式7中のiR7は式10となります.
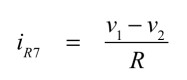 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
以上を使って整理すると,i1の電流は式11となります.
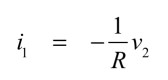 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
次にi2の電流は式12となります.
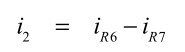 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
式12中のiR6は式13となります.
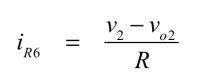 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
式13中のvo2は,OPアンプU2の2つの入力端子はバーチャル・ショートなので,式14となります.
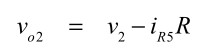 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
式14中のiR5はR4に流れる電流と同じなので,式15となります.
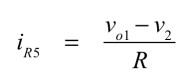 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
以上を使って整理すると,i2の電流は式16になります.
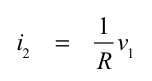 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
式11と式16より,図7に示すジャイレータのv2側を1次側,v1側を2次側と考えれば式6に示した理想ジャイレータの行列式と同じであり,ジャイレッション・コンダクタンスが「G=1/R」のジャイレータとして働くことが分かります.
●ジャイレータによる電圧制御電流源の検証
図3に示したジャイレータの1つめの特徴である電圧制御電流源について,図7のジャイレータを用いて動作を確かめます.先ほど述べたとおり,図7のv1側が2次側,R8の接続箇所が1次側となります.
図8のジャイレッション・コンダクタンスは「G=1/1kΩ=1mA/V」です.シミュレーションはv1を変化させたときの負荷抵抗(R8)に流れる電流を調べます.電圧制御電流源ですので,負荷抵抗の値が変化しても電流は同じにならねばなりません.これを確かめるため,R8の抵抗を「.stepコマンド」を用いて100Ω,470Ω,1kΩと変化させています.
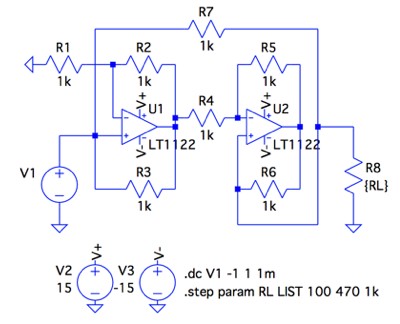
図9がシミュレーション結果です.負荷抵抗(R8)の抵抗を変化させても流れる電流は変わらず,式16に示したv1の電圧で電流が変わる電圧制御電流源になることがわかります.
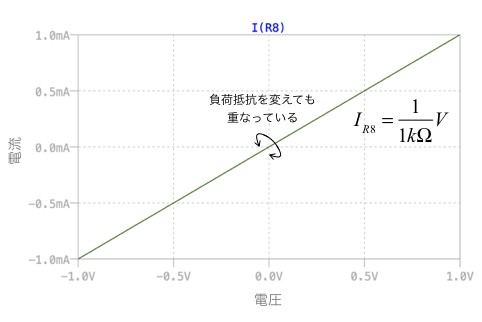
R8からジャイレータ側へ流れ込む電流をプロット.
「G=1/1kΩ」のジャイレッション・コンダクタンスを持つ電圧制御電流源となる.
●ジャイレータによるインダクタの実現
図4に示したジャイレータの2つめの特徴であるインピーダンス変換について確かめます.図10(a)は,図7のジャイレータを使った等価インダクタと抵抗(R8)でLR回路とし,その周波数特性をOUT1端子で調べます.ジャイレッション・コンダクタンスは「.stepコマンド」で値を1kΩ,2.2kΩ,4.7kΩと変え,等価インダクタンスで表すと100mH,484mH,2.209Hに相当します.図10(b)は理想のインダクタ(L1)にジャイレータによる等価インダクタで求まる値を入れ,OUT1とOUT2の周波数特性を比べるのが目的です.
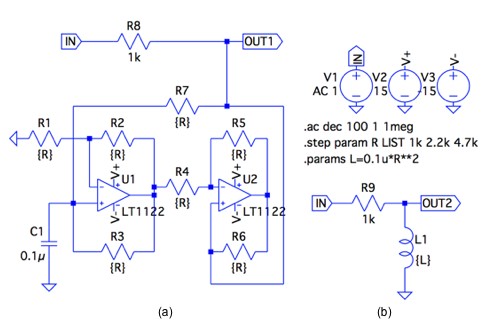
(a) ジャイレータと0.1μFのコンデンサで,大きな等価インダクタを得る回路
(b) (a)の計算値と同等なインダクタを使ったLR回路
図11がシミュレーション結果です.約100kHz以下の周波数帯では,OUT1,OUT2の周波数特性は重なっており,ジャイレータによる等価インダクタは計算通りと分かります.それ以上の高周波側ではOPアンプの周波数特性の影響を受けるため,OUT1とOUT2の周波数特性に誤差が生じます.
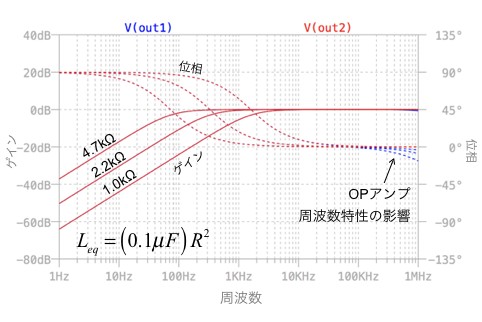
(a)と(b)は重なっており,計算通りの大きなインダクタンスが得られる.また,Gによりインダクタンスの大きさが変わる.
以上,解説したように,ジャイレータのインピーダンス変換を使うと,小さなコンデンサで大きな等価インダクタを得ることができます.ジャイレータ回路は,それを構成するOPアンプ等の周波数特性に依存しますので,低周波用途のフィルタ回路にむいています.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_033.zip
●データ・ファイル内容
Gyrator_Basic.asc:図5の回路
VCCS_realization_via_Gyrator.asc:図8の回路
Inductor_realization_via_Gyrator.asc:図10の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs










